В.И. Вершинин, Р.Ю. Симанчев, Омский государственный университет, кафедра аналитической химии и химии нефти
Постановка задачи.В химической технологии нередко требуется получать композиции с заданными свойствами, смешивая N однотипных компонентов. При этом массовые или объемные доли компонентов подбирают эмпирически в ходе длительных экспериментов или заранее рассчитывают с учетом свойств каждого компонента. Расчеты возможны только в том случае, когда процесс смешивания протекает аддитивно, то есть без химического или какого-либо иного взаимодействия между компонентами. Состав смеси рассчитать тем труднее, чем большее число свойств смеси надо учесть. Например, для получения бензина с октановым числом (ОЧ) = 92 можно смешивать бензины с ОЧ = 76 и ОЧ = 95, и расчет доли каждого из них (xj) не вызывет затруднений. Подбирая же состав бензиновой смеси по четырем свойствам одновременно, например, добиваясь заданных значений ОЧ, температуры вспышки, плотности и предела выкипания, придется смешивать несколько компонентов, а для точного расчета состава смеси решать систему из 4 линейных уравнений с несколькими неизвестными xj. Предварительный выбор возможных компонентов проводится так, чтобы по единичному свойству одни из них имели бы более высокие, а другие - более низкие значения, чем требуемая смесь. Однако это условие - необходимое, но не достаточное; решения должны отвечать естественным ограничениям, а именно: доля любого компонента должна попадать в интервал (0, 1), а сумма xj должна равняться единице. Рассчитать "идеальный" состав смеси "в лоб", то есть решая систему линейных уравнений, удается редко. Несомненно, для подбора качественного и расчета количественного состава аддитивных смесей перспективно применение ЭВМ. Смеси определенного вида (например, нефтепродукты) могут быть рассчитаны с помощью зарубежных многоцелевых лицензионных программ [1], но нам неизвестны программы, позволяющие решать подобные задачи в общем виде с учетом требуемой точности прогноза.
Целью настоящей работы было создание алгоритма и программного обеспечения для нахождения состава аддитивных смесей со свойствами, с определенной степенью точности соответствующими заданному набору значений ("идеалу"). Такой подход объясняется тем, что в процессе приготовления реальных композиций всегда допускаются небольшие отклонения свойств смеси от желаемых значений, связанные, в частности, с неизбежными погрешностями при измерении свойств смеси. Пределы отклонений указываются в технической документации.
Алгоритм и программа. Допустим, что смесь предполагается составлять из N однотипных компонентов, при этом надо контролировать М свойств, имеющих одинаковую значимость. Обозначим численные значения i-го свойства смеси через Ri, а его идеальное значение через Fi. Те же показатели компонентов, взятых порознь, определяют заранее по стандартной методике или берут их из нормативной документации. Обозначим i-й показатель j-го компонента через Pij. Совокупность всех Pij для однотипных компонентов образует базу данных (БД).
Предположение об аддитивном характере смеси означает, что измеренное значение любого свойства (показателя) смеси равно:
|
| (1) |
Пусть Ri -задаваемое пользователем максимально допустимое отклонение i-го показателя смеси от его идеального значения. Будем считать, что допустимые отклонения каждого показателя "вверх" и "вниз" одинаковы, тогда модель аддитивного смешения приводит к системе неравенств и уравнений вида:
|
| (2) |
|
| (3) |
|
| (4) |
Условием существования смеси, отвечающей заданным требованиям, является совместность системы (2)-(4). Для решения этой системы целесообразно применить симплекс-метод [2] с произвольной линейной целевой функцией. В отличие от системы уравнений вида Fi - Pij xj = 0, система (2)-(4), как правило, имеет множество допустимых решений, особенно при больших Ri. Иными словами, приблизительное решение задачи о составе смеси возможно даже в тех случаях, когда точное решение получено быть не может. Приблизительное решение может быть уточнено различными способами, например путем повторных решений системы неравенств при постепенно уменьшающихся значениях Ri. Разумеется, исходная система неравенств может не иметь допустимых решений даже при больших Ri, что указывает на неудачный выбор исходных компонентов смеси, сочетанием которых приготовить смесь с желаемым набором свойств в принципе невозможно. В этом случае следует заменить один из компонентов смеси или ввести дополнительный.
Предложенный алгоритм был реализован (*1) в виде оригинальной расчетной программы Expert" для IBM-совместимых компьютеров с использованием системы программирования Borland С++. Программа "Ехpert" рассчитана на подбор состава смесей до 5-компонентных включительно и может учитывать до 5 независимых показателей. Первый вариант программы не требует наличия компьютерной базы данных и их автоматизированного ввода; свойства компонентов, как и "идеальные" свойства смеси, вводятся вручную. Значения Ri задаются пользователем в процентах от Fi, причем по разным показателям эти проценты могут не совпадать. Пользовательский интерфейс (на русском языке) рассчитан на интерактивный режим, он обеспечивает сохранение, дополнение или корректировку всех введенных параметров, а также выдачу на печать протокола эксперимента. Протокол воспроизводит исходные данные, содержит одно из допустимых решений системы (2)-(4), то есть набор xj, а также результаты подстановки этого решения в формулу (1). При несовместности системы пользователь получает сообщение, что достичь заданной близости свойств композиции к идеалу на основе данного набора компонентов нельзя.
Программа рассчитана на пользователя-технолога, проводящего серию последовательных расчетов (интерактивный режим компьютерного эксперимента). Если имеется база данных по свойствам возможных компонентов, но качественный состав композиции и даже число компонентов в ней заранее не определены, то рекомендуется начинать с проверки наиболее простых композиций. Вначале следует задавать достаточно большие отклонения, например Ri = 0,2 Fi. Отрицательный результат укажет на необходимость немедленно перейти к проверке смеси иного качественного состава, по усмотрению пользователя. В случае положительного результата пользователь может повторять расчет, последовательно уменьшая величину Ri (корректировка условия задачи и единичное решение ее занимают не более минуты). В результате серии расчетов будет получено либо достаточно точное совпадение всех показателей смеси с идеалом, либо выявлен тот набор минимальных значений Ri, ближе которого к идеалу подойти при данном качественном составе смеси нельзя.
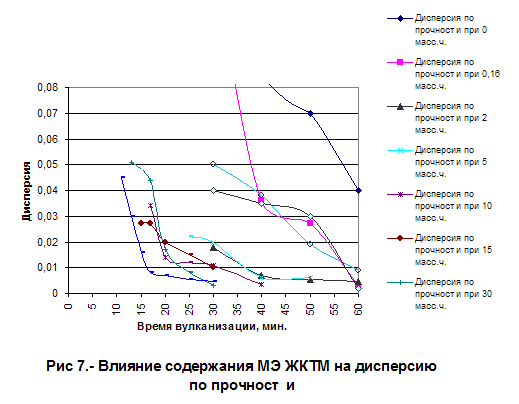
Пример. В производстве определенного вида резины желательно было заменить уникальную импортную сажу А композицией из отечественных саж того же типа (*2). При этом надо было добиться как можно более полного совпадения трех адсорбционных показателей композиции (условно обозначены как , и ) со свойствами А. Аддитивность адсорбционных свойств композиций, составляемых из однотипных саж, ранее была доказана экспериментальным путем [3], что и позволило нам применять вышеописанный алгоритм и программное обеспечение. Вначале проверялась 3-компонентная композиция из саж Б, В и Г, выбранная технологами интуитивно (показатели сажи Б отличаются от А всего на 10% (запись эксперимента прилагается), тогда как сажи В и Г имеют соответственно существенно более высокие и более низкие показатели. Предполагалось, что В и Г могут быть регулирующими добавками. Проверка вначале проводилась при Ri = 0,05 Fi . Как видно из таблицы, составленной на основе информации, выданной ЭВМ на печать, моделирование А 3-компонентной смесью Б, В и Г действительно должно при некоторых их соотношениях приводить к отклонениям, не превышающим 5% отн., например, при доле В = 7,65% и Г = 10,23%. Повторный расчет при Ri = 0,03 Fi показал, что с этой точностью идеал также достигается, но уже при более высоких содержаниях добавок. Однако следующий расчет при Ri = 0,02 Fi не выявил допустимых решений, то есть дальнейшая оптимизация состава и свойств композиции Б, В и Г оказалась невозможной.
Аналогичные расчеты для композиций другого качественного состава привели к принципиально иным прогнозам. Так, было показано, что используя 2-компонентные смеси В и Г, мы при любых их соотношениях будем получать отклонения от идеала, превышающие 5%. Если же смешивать сажи Б и Д, можно при некотором их соотношении ожидать получения композиции, отличающейся от свойств сажи А по всем трем показателям всего на 1% . Так как погрешность измерения адсорбционных показателей в технологии сажевого производства более 1%, мы посчитали процесс оптимизации завершенным. Суммарное время компьютерного эксперимента по перечисленным сажевым композициям не превысило 50 мин.
Для проверки компьютерного прогноза была изготовлена реальная композиции Б + Д с вычисленным соотношением компонентов. Ее свойства исследовались в лабораториях Института техуглерода СО РАН (Омск) по стандартным методикам. Результаты подтвердили совпадение рассчитанных и реально полученных свойств композиции, то есть адекватность модели аддитивного смешения. Судя по экспериментальным данным, расхождения всех показателей композиции со свойствами уникальной сажи типа А не превышали 3% отн. и были статистически незначимы.
Данный пример подтверждает целесообразность применения программы Expert для прогнозирования качественного и количественного состава композиций c заданными свойствами. Возможны дальнейшие усовершенствования программы (можно автоматизировать перебор возможных сочетаний компонентов и ввод их показателей из БД, улучшить процедуру оптимизации и т.п.), однако выигрыш во времени вряд ли будет существенным. С другой стороны, применяемый сейчас интерактивный режим имеет и свои преимущества, в частности, технолог может использовать информацию, не учтенную в БД, уделять преимущественное внимание оптимизации по наиболее важным свойствам композиции и т.п.
| Протокол компьютерного эксперимента Моделирование свойств сажи А композицией Б + В + Г | ||||
| Показатели | Результаты | |||
| | | | ||
| Идеал (А) | 114 | 109 | 106 | |
| Компонент Б | 116 | 106 | 98 | |
| Компонент В | 238 | 159 | 140 | |
| Компонент Г | 61 | 99 | 93 | |
| Расчет 1 | ||||
| Ri, в % | ±5 | ±5 | ±5 | xБ = 0,8212 |
| xВ = 0,0765 | ||||
| xГ = 0,1023 | ||||
| Подстановка | 119,7 | 109,3 | 100,7 | |
| Расчет 2 | ||||
| Ri, в % | ±1 | ±3 | ±3 | xБ = 0,4744 |
| xВ = 0,1585 | ||||
| xГ = 0,3671 | ||||
| Подстановка | 115,1 | 111,8 | 102,8 | |
| Расчет 3 | ||||
| Ri, в % | ±2 | ±2 | ±2 | решений нет |
Современные системы компаундирования моторных топлив: Информационный обзор. М.: ЦНИИНефтехим, 1997.
Схивер А. Теория линейнего целочисленного программирования: В 2 т. М.: Мир, 1991.
Dowdle L.T. Gummi, asbest, kunststoffe. 1978. No 1. С. 51
Похожие работы
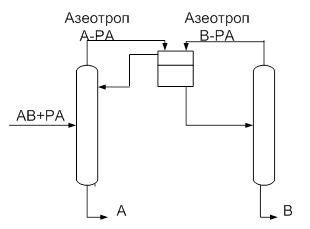
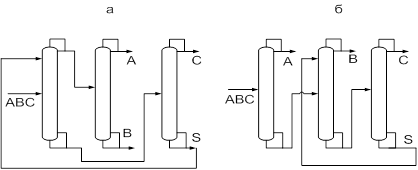
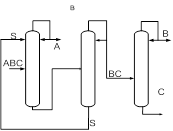
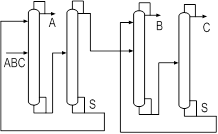
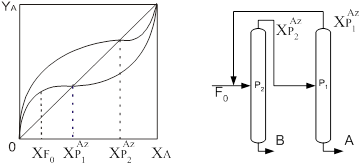
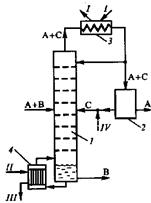
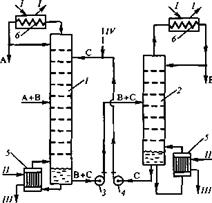
... резкое изменение температуры, обусловленное скачкообразным изменением концентрации РА. [12] Постановка задачи Целью данной работы является поиск оптимальной схемы экстрактивной ректификации смеси бензол-циклогексан-этилбензол-н-пропилбензол, содержащей один бинарный азеотроп. Для этого необходимо выполнить: · параметрическую оптимизацию традиционных схем экстрактивной ректификации; · ...
... вторичным продуктом целлюлозо-бумажной промышленности при получении талловой канифоли методом ректификации таллового масла /37/. 1.5 Исследование таллового масла в качестве заменителя более дорогих технологических добавок На современном этапе рыночных отношений в России проблемы, связанные с разработкой научных основ производства и технологии оформления процессов, а также ассортимента ...
... С целью увеличения выхода и упрощения технологии процесса за счет исключения стадии щелочной промывки из процесса осушки 1,3-диоксолана и повышения экологической чистоты технологии разделения азеотропной смеси 1,3-диоксолан-вода, проводят экстрактивную ректификацию с использованием в качестве экстрагента этиленгликоль. Предлагаемое изобретение может быть использовано для получения 1,3-диоксолана, ...
... , солестойкость, повышенная плотность) в их состав вводят минеральные добавки (шлак, кварцевый песок, известняк) в количестве от 10 до 70 %. 2. Физико-технические свойства строительных материалов Все свойства строительных материалов можно условно разделить на физические, химические, механические и технологические. Физические свойства в свою очередь подразделяют на общефизические, ...
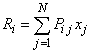
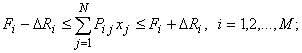
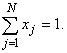

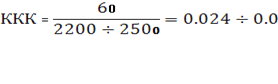
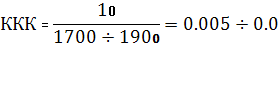
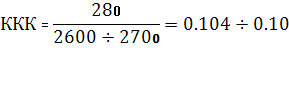
0 комментариев