(практическая работа по компьютерной алгебре)
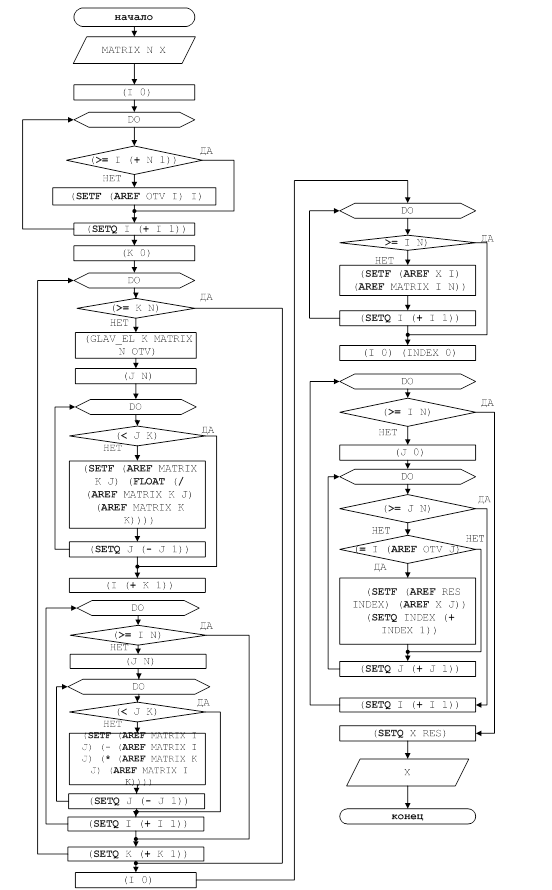
Текст программы.
#include <fstream.h>
#include <math.h>
#include <conio.h>
#include <stdlib.h>
const num = 4;
int i,j,I,J;
int c[num+1];
long double x[num+1];
long double max;
long double A[num][num+1];
// -----------------------------------------------------------
void max_el(int sr, int st)
{ max = A[num+1-sr][num+2-st];
I = num+1-sr;
J = num+2-st;
for (i = num+1-sr ; i<=num ; i++)
{
for (j = num+2-st ; j<=num ; j++)
{
if (fabs(A[i][j]) > fabs(max))
{
max = A[i][j];
I = i;
J = j;
}
}
}
cout << "\n\n Max = " << max << " I=" << I<< " J=" << J;
}
// -----------------------------------------------------------
void print(int sr,int st)
{
cout << "\n";
int i,j;
for (i = num+1-sr ; i<=num ; i++)
{
for (j = num+2-st ; j<=num+1 ; j++)
{
if (A[i][j] < 0 ) gotoxy(12*j + j - 1,i+1);
else gotoxy(12*j + j,i+1);
cout << A[i][j];
}
}
}
// ------------------------------------------------------------------
void preob(int S)
{
int i,j;
long double temp;
for (j = S; j<=num+1; j++) A[S][j] = A[S][j]/max;
for (i = S + 1; i <= num; i++)
{
temp = A[i][S];
for (j = S; j<= num+1 ; j++) A[i][j] = A[i][j] - A[S][j]*temp;
}
}
// ------------------------------------------------------------------
void perestanovka(int sr,int st)
{
if (J != (num+1-sr))
{
for (i = 1; i<=num; i++) {
A[i][J] = A[i][J] + A[i][num+1-sr];
A[i][num+1-sr] = A[i][J] - A[i][num+1-sr];
A[i][J] = A[i][J] - A[i][num+1-sr];
}
c[J] = c[J] + c[num+1-sr];
c[num+1-sr] = c[J] - c[num+1-sr];
c[J] = c[J] - c[num+1-sr];
}
if (I != (num+2-st))
{
for (j = 1; j<=num+1; j++) {
A[I][j] = A[I][j] + A[num+2-st][j];
A[num+2-st][j] = A[I][j] - A[num+2-st][j];
A[I][j] = A[I][j] - A[num+2-st][j]; }
}
}
// ------------------------------------------------------------------
void otvet()
{
float temp;
for (i=num; i>=1; i--)
{
temp = A[i][num+1];
for(j = num; j > i; j--) temp = temp - A[i][j]*x[j];
x[i] = temp/A[i][i];
}
}
// ------------------------------------------------------------------
void interface()
{
clrscr();
print(num,num+1);
cout << "\n Массив перестановок столбцов ";
for (i = 1; i <= num ;i++) cout << " " << c[i];
}
// ------------------------------------------------------------------
void load_file()
{
char ch;
ifstream in("c:\\gauss\\mat.dat");
cout << "\n";
for (i = 1 ; i<=num ; i++)
{
c[i] = i;
while (ch != '') in >> ch;
ch = 'q';
for (j = 1 ; j<=num+1 ; j++) in >> A[i][j];
}
}
// ------------------------------------------------------------------
void main()
{
clrscr();
load_file();
int g;
for(g = num+1; g >= 3; g--)
{
interface(); max_el(g-1,g); getch();
perestanovka(g-1,g); interface(); getch();
preob(num+2-g); interface(); getch();
}
clrscr();
print(num,num+1);
otvet();
print(num,num+1);
cout << "\n\n ";
long double X[num];
for (i=1; i<=num; i++) X[c[i]] = x[i];
for (i=1; i<=num; i++) cout << " X" << i << " = " << X[i];
getch();
}
Тестовые задания.
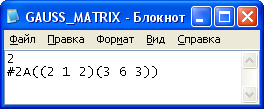
Задание №1 (найти неизвестные):
4.24x1 + 2.73x2 - 1.55x3 = 1.87
2.34x1 + 1.27x2 + 3.15x3 = 2.16
3.05x1 - 1.05x2 - 0.63x3 = -1.25
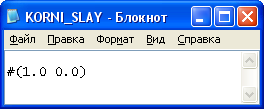
1.1 Результат выполнения программы:
x1 = - 0.025461 x2 = 0.915112 x3 = 0.335678
1.2 Расчёт погрешности вычисления:
4.24*(- 0.025461) + 2.73*0.915112 - 1.55*0.335678 = 1,87000022 погрешность:
2,2*10-7
2.34*(- 0.025461) + 1.27*0.915112 + 3.15*0.335678 = 2,1599992 погрешность:
8,0*10-7
3.05*(- 0.025461) - 1.05*0.915112 - 0.63*0.335678 = -1,25000079 погрешность:
7,9*10-7
средняя погрешность вычисления: 6,0*10-7
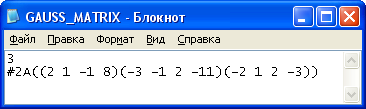
Задание №2 (найти неизвестные):
3.81x1 + 0.25x2 + 1.28x3 + (0.75+a)x4 = 4.21
2.25x1 + 1.32x2 + (4.5+a)x3 + 0.49x4 = 6.47+b
5.31x1 + (0.28+a) x2 + 0.98x3 + 1.04x4 = 2.38
(9.39+a)x1 + 2.45x2 + 3.35x3 + 2.28x4 = 10.48+b
a = (0,1,2,3,4) b = (0,1,2,3,4,5)
2.1 Таблица значений.
abОтветы:
00X1 = -12.660899
X2 = -16.107649
X3 = 5.273899
X4 = 66.299137
1X1 = -12.132586
X2 = -14.858407
X3 = 5.186943
X4 = 63.347289
2X1 = -11.604272
X2 = -13.609166
X3 = 5.099988
X4 = 60.39544
3X1 = -11.075957
X2 = -12.359925
X3 = 5.013031
X4 = 57.443595
4X1 = -10.547642
X2 = -11.110685
X3 = 4.926076
X4 = 54.491746
5X1 = -10.019327
X2 = -9.861445
X3 = 4.839121
X4 = 51.539901
10X1 = 13.959632
X2 = -39.106359
X3 = 7.324007
X4 = -27.756765
1X1 = 16.668562
X2 = -46.672114
X3 = 8.73446
X4 = -33.605312
2X1 = 19.377489
X2 = -54.237864
X3 = 10.144913
X4 = -39.453861
3X1 = 22.086416
X2 = -61.803618
X3 = 11.555367
X4 = -45.30241
4X1 = 24.795347
X2 = -69.369373
X3 = 12.96582
X4 = -51.150959
5X1 = 27.504276
X2 = -76.935127
X3 = 14.376274
X4 = -56.999508
20X1 = 1.033843
X2 = -1.696273
X3 = 0.997951
X4 = -0.211727
1X1 = 1.191176
X2 = -2.016845
X3 = 1.183171
X4 = -0.486773
2X1 = 1.348508
X2 = -2.337417
X3 = 1.36839
X4 = -0.761819
3X1 = 1.505841
X2 = -2.657989
X3 = 1.55361
X4 = -1.036865
4X1 = 1.663174
X2 = -2.978561
X3 = 1.73883
X4 = -1.311911
5X1 = 1.820507
X2 = -3.299134
X3 = 1.92405
X4 = -1.586957
30X1 = 0.772977
X2 = -0.794749
X3 = 0.762146
X4 = 0.13016
1X1 = 0.872765
X2 = -0.954303
X3 = 0.902687
X4 = -0.008559
2X1 = 0.972553
X2 = -1.113856
X3 = 1.043229
X4 = -0.147278
3X1 = 1.072341
X2 = -1.27341
X3 = 1.18377
X4 = -0.285998
4X1 = 1.172129
X2 = -1.432964
X3 = 1.324311
X4 = -0.424717
5X1 = 1.271917
X2 = -1.592518
X3 = 1.464853
X4 = -0.563436
40X1 = 0.675128
X2 = -0.476895
X3 = 0.645225
X4 = 0.196021
1X1 = 0.754634
X2 = -0.580642
X3 = 0.763131
X4 = 0.105936
2X1 = 0.83414
X2 = -0.68439
X3 = 0.881037
X4 = 0.015852
3X1 = 0.913647
X2 = -0.788137
X3 = 0.998942
X4 = -0.074233
4X1 = 0.993153
X2 = -0.891884
X3 = 1.116848
X4 = -0.164317
5X1 = 1.072659
X2 = -0.995631
X3 = 1.234754
X4 = -0.254402
Похожие работы
... треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода. Целью данной курсовой работы является численное решение системы линейных уравнений с помощью метода исключения Гаусса с выбором главного элемента по столбцу. 1 Постановка задачи Задача ставится следующим образом. Пусть требуется найти решение системы линейных алгебраических уравнений a1,1x1 + a1, ...
... 1.2 0.4 -0.8 -0.8 3.6 4 4.7 10.4 9.7 9.7 -8.4Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = ...
... лежащие на главной и двух побочных диагоналях, равны нулю при та В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных. Т.е. матрицу А можно записать Идея метода прогонки состоит ...
... уравнений (2) сводится к последовательному решению двух следующих систем уравнений с треугольными матрицами коэффициентов L Y = B; (6) U X = Y (7) линейный алгебраический уравнение численный где Y = - вектор вспомогательных переменных. Такой подход позволяет многократно решать системы линейных ...

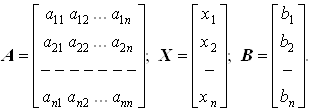



0 комментариев