Навигация
Численные методы линейной алгебры
Содержание
Введение
1. Метод Гаусса
2. Модификации метода Гаусса
3. Метод прогонки
4. Вычисление определителей
5. Вычисление обратных матриц
6. Итерационные методы
Заключение
Список литературы
Введение
Основной целью реферата является изучение и сравнительный анализ численных методов решения систем линейных алгебраических уравнений, вычисления определителей и обратных матриц; реализация этих методов в виде машинных программ на языке высокого уровня и практическое решение задач на ЭВМ.
В общем случае система линейных алгебраических уравнений имеет вид
 (1)
(1)
В матричной форме система (1) представляется как
A X = B (2)
где
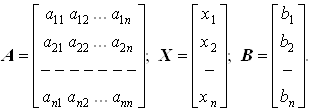
Чтобы такая система уравнений имела единственное решение, входящие в нее n уравнений должны быть линейно независимыми. Необходимым и достаточным условием этого является неравенство нулю определителя данной системы, т.е. det A ¹ 0. Алгоритмы решения систем уравнений такого типа делятся на прямые и итерационные.
1. Метод Гаусса
Данный метод также называется методом последовательного исключения неизвестных. Он относится к группе прямых методов и основан на преобразовании исходной системы к эквивалентной форме с треугольной матрицей коэффициентов.
При использовании метода Гаусса задача решается в два этапа:
1) прямой ход;
2) обратный ход.
Прямой ход заключается в преобразовании системы к треугольному виду.
При обратном ходе производится вычисление значений неизвестных.
Прямой ход метода Гаусса. Для получения расчетных формул прямого хода преобразуем исходную систему (1), заменив элементы bi (![]() ) на ai,n+1. В результате система (1) будет иметь следующий вид
) на ai,n+1. В результате система (1) будет иметь следующий вид

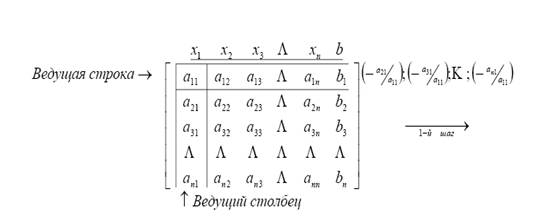
Прямой ход выполняется за (n-1) шагов, причем на каждом шаге из уравнений с номерами k + 1, k + 2, …, n исключается неизвестное xk.
На первом шаге сначала первое уравнение делится на a11 ¹ 0. Получим
![]() (3)
(3)
где 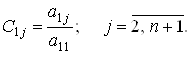
![]() (
(![]() )
)
вычитается полученное уравнение (3), умноженное на коэффициент ai1. В итоге, после выполнения первого шага прямого хода система уравнений примет следующий вид
 (4)
(4)
где
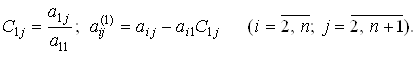
На втором шаге указанные выше действия повторяются над (n - 1) уравнениями системы (4), всеми кроме первого, с целью исключения переменной x2, где
![]()
В итоге получим

где
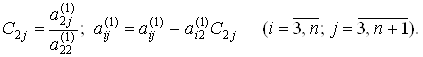
Повторяя шаги прямого хода (n - 1) раз, окончательно получим систему уравнений треугольного вида
 (5)
(5)
где
![]()
При программной реализации прямого хода используется расширенная матрица коэффициентов A¢
 ,
,
для которой элементы имеют следующий смысл
1) ![]() - начальные значения;
- начальные значения;
2) ![]() - промежуточные значения;
- промежуточные значения;
3) ![]() - конечные значения.
- конечные значения.
Для определения элементов ![]() матрицы A¢ на некотором k-ом шаге
матрицы A¢ на некотором k-ом шаге
(![]() )
)
используются следующие расчетные формулы
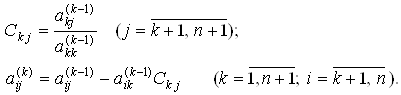
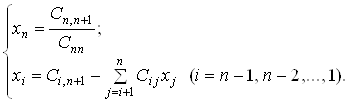
Обратный ход метода Гаусса. После приведения исходной системы уравнений (1) к треугольному виду (5) вычисляются значения корней по следующим формулам

Таким образом, расчетные формулы обратного хода имеют вид
Вычислительная сложность метода Гаусса оценивается как O(n3), причем для реализации прямого хода требуется около ![]() арифметических операций, а для обратного – около n2 операций.
арифметических операций, а для обратного – около n2 операций.
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
... на языке Turbo Pascal 7.0 для решении систем линейных алгебраических уравнений, используя метод простой итерации. 1.2 Математическая формулировка задачи Пусть А – невырожденная матрица и нужно решить систему где диагональные элементы матрицы А ненулевые. 1.3 Обзор существующих численных методов решения задачи Метод Гаусса В методе Гаусса матрица СЛАУ с помощью равносильных ...
... числа). Далее по формулам (2) последовательно находятся xn-1 , xn-2 ,…, x1 при i=n-1, n-2,...,1 соответственно. Таким образом, решение уравнений вида (1) описываем способом, называемым методом прогонки, сводится к вычислениям по трём простым формулам: нахождение так называемых прогоночных коэффициентов δi, λiпо формулам (3) при i=1,2,…,n (прямая прогонка) и затем неизвестных xi по ...

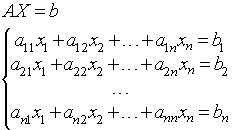
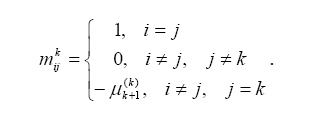
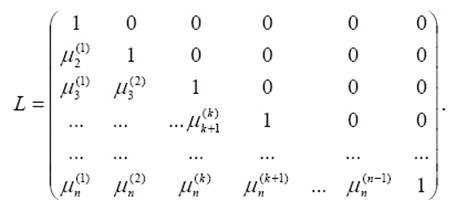
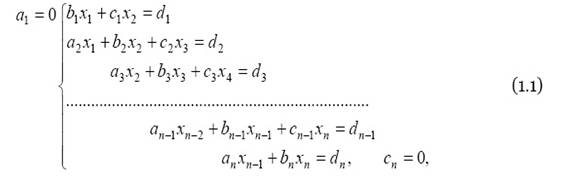
0 комментариев