Навигация
АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
8. АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Решая задачу симплекс методом мы получили:
Детали A1 так относятся к деталям A2, как 2:1, т.е. деталей A1 – 30 штук, а деталей A2 – 15 штук. Соотношение, поставленное условием задачи, выполнено.
Соотношение между деталями A3 и A4 тоже выполнено. Детали A3 должны относиться к деталям A4 как 4:1. Это верно, так как деталей A3 – 292 штуки, а деталей A4 – 73 штуки.
Но на третьей группе оборудования идет недоиспользование ресурсов на 20 станко-часов.
Максимально возможная загрузка имеющегося оборудования – 410 деталей.
При решении с помощью компьютера получились более точные результаты, которые приблизительно равны ручным.
9. ИНСТРУКЦИИ ПОЛЬЗОВАТЕЛЮ И ОПИСАНИЕ
ПРОГРАММЫ
Данная программа используется в графической оболочке KoSer, которая была написана мною для олимпиады по программированию. Эта оболочка имеет интерфейс, чем-то напоминающий WINDOWS.
К данной курсовой работе прилагается инсталляционная дискета с данной оболочкой и программой SIMPLEX.
Она может быть установлена в двух типах:
Для преподавателя, устанавливается с текстами программ.
Для пользователей, только запускаемые модули.
В любом случае вы запускаете ТОЛЬКО файл KoSer.EXE. У вас запустится графическая оболочка.
В этой оболочке будут следующие иконки:
Simplex Method, это сама программа для решения уравнений.
Просмотр результатов, Чтобы просмотреть результат после решения.
Tetris, обычная игра для развлечения.
MsDos, Временный выход в DOS
Exit, выход из оболочки KoSer.
В программе «Simplex Method» есть кнопки «Добавить строку», «Добавить столбец», «Удалить строку», «Удалить столбец», «Рассчитать», «Решить на MAX или MIN», «Решение ЦЕЛОЧИСЛЕННОЕ или НЕ ЦЕЛОЧИСЛЕННОЕ».
Переход к этим кнопкам осуществляется клавишей «TAB» или (рекомендуется) с помощью мышки.
Движение по числовым значениям уравнения осуществляется стрелками. Ввод чисел производится просто набором цифр на данной ячейки.
Смена знака осуществляется клавишей «пробел».
Выход – крестик в верхнем углу экрана или клавиша «ESC».
ЗАКЛЮЧЕНИЕ
Данная курсовая работа включает в себя два предмета: «языки программирования» и «математические методы в экономике».
В курсовой работе были рассмотрены следующие вопросы:
Рассмотрен и дан алгоритм симплекс метода.
Дана краткая характеристика ЭВМ, включая историю появления и описание операционной системы MSDOS.
Рассмотрен выбор языка программирования.
Написана программа для решения данной и многих других задач.
Даны инструкции пользователю.
Данная программа была протестирована на очень многих примерах и везде она выдавала правильные результаты.
Единственное ограничение, количество столбцов не должно превышать 7 и строк не должно превышать 10.
Программа считает с точностью 2 знака после запятой.
Список используемой литературы:
Лищенко «Линейное и нелинейное программирование», 1987
А.Н. Карасев, Н.Ш. Кремер, Т.Н. Савельева
«Математические методы в экономике», 1987
ПРИЛОЖЕНИЯ
Приложение 3
ЛИСТИНГ РЕЗУЛЬТАТОВ ПРОГРАММЫ Simplex Method
C Б H X1 X2 X3 X4 X5 X6 X7 Y1 Y2
0.00 X5 760.00 1.20 1.80 2.40 0.00 1.00 0.00 0.00 0.00 0.00
0.00 X6 600.00 2.40 0.00 1.20 2.40 0.00 1.00 0.00 0.00 0.00
0.00 X7 480.00 0.00 1.20 1.20 1.20 0.00 0.00 1.00 0.00 0.00
+M Y1 0.00 1.00 -2.00 0.00 0.00 0.00 0.00 0.00 1.00 0.00
+M Y2 0.00 0.00 0.00 1.00 -4.00 0.00 0.00 0.00 0.00 1.00
0.00 1.00 -2.00 1.00 -4.00 0.00 0.00 0.00 0.00 0.00
Ключевой столбец: 3 Ключевая строка: 5
C Б H X1 X2 X3 X4 X5 X6 X7 Y1
0.00 X5 760.00 1.20 1.80 0.00 9.60 1.00 0.00 0.00 0.00
0.00 X6 600.00 2.40 0.00 0.00 7.20 0.00 1.00 0.00 0.00
0.00 X7 480.00 0.00 1.20 0.00 6.00 0.00 0.00 1.00 0.00
+M Y1 0.00 1.00 -2.00 0.00 0.00 0.00 0.00 0.00 1.00
-1.00 X3 0.00 0.00 0.00 1.00 -4.00 0.00 0.00 0.00 0.00
0.00 1.00 -2.00 0.00 0.00 0.00 0.00 0.00 0.00
Ключевой столбец: 1 Ключевая строка: 4
C Б H X1 X2 X3 X4 X5 X6 X7
0.00 X5 760.00 0.00 4.20 0.00 9.60 1.00 0.00 0.00
0.00 X6 600.00 0.00 4.80 0.00 7.20 0.00 1.00 0.00
0.00 X7 480.00 0.00 1.20 0.00 6.00 0.00 0.00 1.00
-1.00 X1 0.00 1.00 -2.00 0.00 0.00 0.00 0.00 0.00
-1.00 X3 0.00 0.00 0.00 1.00 -4.00 0.00 0.00 0.00
0.00 0.00 3.00 0.00 5.00 0.00 0.00 0.00
Ключевой столбец: 4 Ключевая строка: 1
C Б H X1 X2 X3 X4 X5 X6 X7
-1.00 X4 79.17 0.00 0.44 0.00 1.00 0.10 0.00 0.00
0.00 X6 30.00 0.00 1.65 0.00 0.00 -0.75 1.00 0.00
0.00 X7 5.00 0.00 -1.43 0.00 0.00 -0.63 0.00 1.00
-1.00 X1 0.00 1.00 -2.00 0.00 0.00 0.00 0.00 0.00
-1.00 X3 316.67 0.00 1.75 1.00 0.00 0.42 0.00 0.00
-395.83 0.00 0.81 0.00 0.00 -0.52 0.00 0.00
Ключевой столбец: 2 Ключевая строка: 2
C Б H X1 X2 X3 X4 X5 X6 X7
-1.00 X4 71.21 0.00 0.00 0.00 1.00 0.30 -0.27 0.00
-1.00 X2 18.18 0.00 1.00 0.00 0.00 -0.45 0.61 0.00
0.00 X7 30.91 0.00 0.00 0.00 0.00 -1.27 0.86 1.00
-1.00 X1 36.36 1.00 0.00 0.00 0.00 -0.91 1.21 0.00
-1.00 X3 284.85 0.00 0.00 1.00 0.00 1.21 -1.06 0.00
-410.61 0.00 0.00 0.00 0.00 -0.15 -0.49 0.00
В 5 -й итерации было получено оптимальное решение
т.к. при исследовании на МИНИМУМ индексная строка не содержит положительных элементов.
При этом:
Fmax= 410.61
X4= 71.21
X2= 18.18
X7= 30.91
X1= 36.36
X3= 284.
Похожие работы
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... и подставляя её во всех остальных равенствах и неравенствах (а также в функции f).Такую задачу называют «основной» или «стандартной» в линейном программировании. 1.2 Решение задач линейного программирования симплекс-методом Задача ЛП в общем виде может быть записана так: (c, x) − max Ax = b, где c =(c1,c2,...,cn)T – мерный вектор-столбец коэффициентов; x =(x1,x2,...,xn)T – ...
... под названием метода обратной матрицы или модифицированного симплекс-метода. При решении задач линейного программирования, в которых n (количество переменных) существенно больше m (количество ограничений), улучшенный симплекс-метод требует по сравнению с другими значительно меньшего количества вычислительных операций и объема памяти ЭВМ. В улучшенном симплекс-методе реализуется та же основная ...
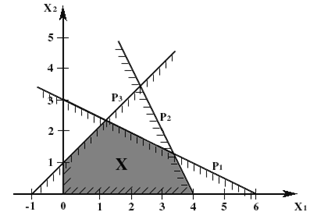
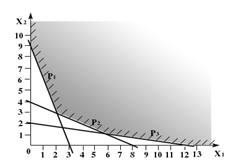
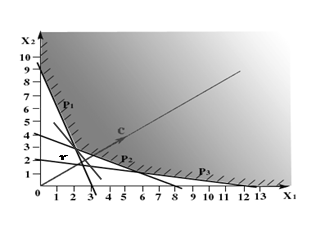
... ограничения несовместны, множество планов пусто и задача ЛП решения не имеет. Рис. 1.4 Рис. 1.5 Рис. 1.6 2. Симплекс-метод 2.1 Идея симплекс-метода Рассмотрим универсальный метод решения канонической задачи линейного программирования , , , с n переменными и m ограничениями-равенствами, известный как симплекс-метод. Множество планов канонической задачи – ...

0 комментариев