Блок (линейный участок)

3.1. Блок (линейный участок)

Вопросы оптимизации обычно связаны с топологией програм­мы, т.е. со способом ее построения. Для того, чтобы локализо­вать процессы оптимизации и не связывать их с конкретным вход­ным языком, они проводятся внутри отдельных участков програм­мы, называемых блоками и сильно связанными областями.

Блок (линейный участок) - выполняемая по порядку последо­вательность операторов, имеющая единственную точку входа - первый оператор с меткой, на который может быть передано уп­равление, и единственную точку выхода - последний оператор.

Блок моделирует часть программы на промежуточном языке, которая содержит операторы присваивания.

Формально модель линейного участка может быть представле­на следующим образом:

блок B - это тройка вида (P,I,U),где

(1) P - список операторов S1,S2,...Sn (n>=0),

(2) I - множество входных переменных,

(3) U - множество выходных переменных.

При этом оператором называется цепочка (в общем случае) вида

A <--QB1...Br,

где A,B1,...,Br - переменные,Q - операция.

Здесь оператор присваивает значение переменной А и ссыла­ется на B1,...,Br.

Если оператор Sj ссылается на А, то либо А--входная пере­менная, либо осуществлено присваивание ей значения некоторым оператором до Sj, (т. е. некоторым оператором Si,(i<j) . Таким образом, внутри ,блока все переменные, на которые ссылаются, к этому моменту определены либо внутренним образом как перемен­ные, которым присвоены значения, либо внешним как входные пе­ременные. Аналогично каждая выходная переменная либо является входной переменной, либо ей присвоено значение некоторым опе­ратором.

Оператор S в программе называется входом в линейный участок, если он либо первый оператор в программе, либо поме­чен идентификатором, появляющимся в операторе перехода, либо непосредственно следует за условным оператором.

Линейный участок, относящийся к входу в участок S, состо­ит из S и всех операторов, следующих за ним вплоть до операто­ра останова, включая его, или вплоть до входа в следующий блок.

3.2. Сильно связанная область

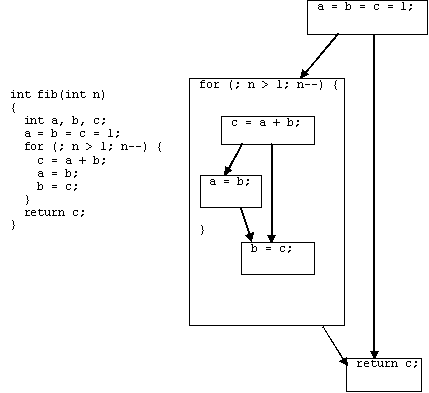
Для каждого блока B=(P,I,U) можно найти ориентированный ациклический граф , представляющий этот блок. При этом каждый лист графа (концевая вершина) соответствует одной входной пе­ременной в I, а каждая его внутренняя вершина - оператору из

P. Граф отражает порядок выполнения операторов программы и да­ет более наглядное представление, чем линейная последователь­ность операторов.

Если вершины i и j графа соответствуют участкам i и j программы, то дуга идет из i в j, если

1) последний оператор участка i не является ни оператором перехода, ни оператором останова, а участок j следует в программе за участком i или

2) последний оператор участка i является оператором пере­хода на метку L, которой помечен первый оператор участка j.

Сильно связанной областью направленного графа называется такое множество его вершин, что для любых двух вершин x и y (x != y) существует путь из x в y.

Будем рассматривать сильно связанные области Ri, обладаю­щие следующими свойствами:

1) Ri является сильносвязанной областью, состоящей из множества блоков, каждый из которых предшествует сам себе и следует сам за собой внутри этого множества;

2) Ri != Rj;

3) для каждого i<j или пересечение Ri и Rj пусто, или Ri является подобластью Rj (включена в нее).

4. Способы оптимизации

Различают две категории оптимизирующих преобразований: преобразования исходной программы в ее внутренней форме, кото­рые не зависят от объектного языка (машинно-независимые) и преобразования, осуществляемые на уровне объектной программы (машинно-ориентированные).

Методы первой категории применимы почти к любому алгебра­ическому языку - ФОРТРАНу, АЛГОЛу, PL/1 и.т.д.

На практике используется весьма широкий набор машинно-не­зависимых оптимизирующих преобразований, что связано с большим разнообразием неоптимальностей. К ним относятся:

- разгрузка участков повторяемости;

- упрощение действий;

- реализация действий;

- чистка программы;

- экономия памяти;

- сокращение программы.

4.1. Разгрузка участков повторяемости

Такое название получил способ оптимизации, состоящий в вынесении вычислений из многократно проводимых (исполняемых ) участков программы на участки программы , редко проходимые.

К этому виду преобразований относятся различные чистки зон, тел циклов и тел рекурсивных процедур, когда инвариантные (по результату выполнения) в соответствующих участках повторя­емости выражения, линейные компоненты (т. е. гамаки, обяза­тельно исполняемые при каждом прохождении участка повторяе­мости) выносятся из него и размещаются перед входом в участок повторяемости - чистка вверх,- или когда уничтожающие свои предыдущие результаты линейные компоненты или группы линейных компонент участка повторяемости выносятся из него и размеща­ются за выходы из участка повторяемости - чистка вниз.

При чистке вверх вынесенные вычисления образуют новый не­посредственный обязательный предшественник участка повторяе­мости, а при чистке вниз - непосредственный обязательный пре­емник участка повторяемости.

Обычно выносятся только такие выражения и линейные фраг­менты программы, которые обязательно исполняются при каждом прохождении разгружаемого участка повторяемости.

Примеры.

а) Чистка вниз преобразует цикл

для K:=1, K+1 пока K<=100

цикл

начало

X:=X*K;

если Z>0 то Y:=sin(X);

иначе A[I]:=X+2;

конец

к виду

для K:=1, K+1 пока K<=100

цикл X:=X*K;

если Z>0 то Y:=sin(X);

иначе A[I]:=X+2;

б) Чистка вверх преобразует цикл

для K:=1, K+1 пока K<=100

цикл

начало

если Z>0 то Y:=1;

иначе Y:=Z+2;

X[K]:=X[K] - Y; конец

к виду

если Z>0 то Y:=1;

иначе Y:=Z+2;

для K:=1, K+1 пока K<=100

цикл X[K]:=X[K] - Y;

Примером чистки тела рекурсивной функции может быть сле­дующий:

тело рекурсивной функции

цел функция Ф(N)

начало

целые Z,W;

W:=1;

если X>0 то W:=Y;

если N<=0 то Ф:=1

иначе

начало

Z:=N-W; Ф:=Z*Ф(Z) конец

конец

содержит два инвариантных гамака, в результате вынесения которых может быть получена следующая функция:

цел функция Ф(N)

начало

целое N;

цел функция F(M)

начало

целое Z;

если M<=0 то F:=1;

иначе

начало

Z:=M-W; F:=Z*F(Z) конец

конец

W:=1;

если X>0 то W:=Y;

Ф:=F(N); конец;

В группу разгрузок участков повторяемости также входят и различные преобразования, которые осуществляют перемещение га­мака по пути, ведущему к месту использования его результатов. При таком преобразовании в отличие от чисток гамак остается в тех же зонах, циклах и процедурах.

Например, с помощью этих преобразований фрагмент

для K:=1, K+1 пока K<=100

цикл

начало

N:=A[K];

если N>0 то переход на L; N:=N*N;

L: если Z=0 то ВЫВОД(N); конец

N:=100;

может быть преобразован к виду:

для K:=1, K+1 пока K<=100

цикл

если Z=0 то

начало

N:=A[K];

если N>0 то переход на L; N:=N*N;

L: ВЫВОД(N); конец;

N:=100;