Навигация
4. Двоичные деревья
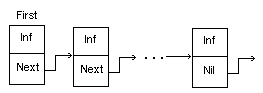
Элементы двоичного дерева помимо информативной части имеют две ссылки √ на нижний левый и на нижний правый элементы. Принцип построения двоичного дерева заключается в том, что очередной элемент в зависимости от значения информативной части должен попасть в правое (если информационная часть включаемого элемента больше информационной части корня) или левое (в противном случае) поддерево. При этом в рамках выбранного поддерева определение местоположения нового элемента производится аналогично (см. рис. 7).
Данную структуру целесообразно описать следующим образом:
type
TypeOfElem= {};
Assoc= ^ElemOfTree;
ElemOfTree= record
Elem: TypeOfElem;
Left, Right: Pointer
end;
4.1 Поиск элемента в дереве
function FoundInTree( Elem: TypeOfElem; var Tree, Result: Pointer ): Boolean;
var
ServiceVar: Assoc;
b: Boolean;
begin
b:= False;
ServiceVar:= Tree;
if Tree <> nil then
repeat
if ServiceVar^.Elem= Elem then b:= True
else
if Elem < ServiceVar^.Elem then ServiceVar:= ServiceVar^.Left
else ServiceVar:= ServiceVar^.Right
until b or ( ServiceVar= nil );
FoundInTree:= b;
Result:= ServiceVar
end;
4.2 Включение элемента в дерево
Включение элемента в дерево реализуется путем во-первых, поиска вершины √ предка нового элемента, во-вторых, непосредственным включением элемента в дерево по найденной позиции. Опишем процедуру поиска предка для нового элемента.
function SearchNode( Elem: TypeOfElem; var Tree, Result: Assoc): Boolean;
var
ServiceVar1, ServiceVar2: Assoc;
b: Boolean;
begin
b:= False;
ServiceVar1:= Tree;
if Tree <> nil then
repeat
ServiceVar2:= ServiceVar1;
if ServiceVar1^.Elem= Elem then {элемент найден} b:= True
else begin
{запоминание обрабатываемой вершины}
ServiceVar2:= ServiceVar1;
if Elem < ServiceVar1^.Elem then ServiceVar1:=
ServiceVar1^.Left
else ServiceVar1:= ServiceVar1^.Right
end
until b or ( ServiceVar1= nil );
SearchNode:= b;
Result:= ServiceVar2
end;
Как видно из описания, эта функция подобна ранее рассмотренной функции поиска элемента дерева (FoundInTree), но в качестве побочного эффекта фиксируется ссылка на вершину, в которой был найден заданный элемент (в случае успешного поиска), или ссылка на вершину, после обработки которой поиск прекращен (в случае неуспешного поиска). Сама процедура включения элемента в дерево будет иметь следующее описание.
procedure IncludeInTree( Elem: TypeOfElem; var Tree: Assoc );
var
Result, Node: Assoc;
begin
if not SearchNode( Elem, Tree, Result ) then begin
{формирование новой вершины в дереве}
new( Node );
Node^.Elem:= Elem;
Node^.Left:= nil;
Node^.Right:= nil;
if Tree= nil then
{если дерево пусто, то созданный элемент сделать вершиной дерева}
Tree:= Node
else
{подсоединить новую вершину к дереву}
if Elem < Result^.Elem then Result^.Left:= Node
else Result^.Right:= Node
end
end;
Двоичное дерево можно рассматривать как рекурсивную структуру данных, состоящую из корневой записи, указывающей на левое и правое поддерево. Оба поддерева имеют такую же структуру: корень поддерева и правое и левое поддеревья. При этом, для представления дерева рекурсивной динамической структурой целесообразно модифицировать описание типа дерева, данное выше. А именно, удобнее изменить тип ссылок на левое и правое поддеревья с нетипизированного (Pointer) на типизированный:
type
TypeOfElem1= {};
Assoc1= ^ElemOfTree1;
ElemOfTree1= record
Elem: TypeOfElem1;
Left, Right: Assoc1
end;
Опишем процедуру вставки элемента рекурсивно.
procedure IncludeInTree2( NewElem: Assoc1; var SubTree: Assoc1 );
begin
if SubTree= nil then begin
SubTree:= NewElem;
NewElem^.Left:= nil;
NewElem^.Right:= nil;
end
else
if NewElem^.Elem < SubTree^.Elem then
IncludeInTree2( NewElem, SubTree^.Left )
else
IncludeInTree2( NewElem, SubTree^.Right )
end;
4.3 Удаление элемента дерева
Проблема реализации данной операции состоит в том, что в общем случае, в удаляемую вершину входит одна связь, а выходят две. Поэтому, необходимо найти подходящий элемент дерева, который можно было бы вставить на место удаляемого. Этот элемент является либо самым правым элементом левого поддерева (для достижения этого элемента необходимо перейти в следующую вершину по левой ветви, а затем, переходить в очередные вершины по правым ветвям до тех пор, пока очередная такая ссылка не будет равна nil), либо самый левый элемент правого поддерева (для достижения этого элемента необходимо перейти в следующую вершину по правой ветви, а затем, переходить в очередные вершины по левым ветвям до тех пор, пока очередная такая ссылка не будет равна nil). Процедура исключения элемента из двоичного дерева должна различать тои случая:
1. элемента с заданной информативной частью в дереве нет; 2. элемент с заданной информативной частью имеет не более одной ветви; 3. элемент с заданной информативной частью имеет две ветви.
procedure DeleteElemOfTree( var Tree: Assoc1; Elem: TypeOfElem1 );
var
ServiceVar1: Assoc1;
procedure Del( var ServiceVar2: Assoc1 );
begin
if ServiceVar2^.Right= nil then begin
ServiceVar1^.Elem:= ServiceVar2^.Elem;
ServiceVar1:= ServiceVar2;
ServiceVar2:=ServiceVar2^.Left
end
else Del( ServiceVar2^.Right )
end;
begin
{удаление элемента с информативным полем равным Elem из дерева Tree}
if Tree= nil then
{первый случай процедуры удаления}
writeln( 'Элемент не найден' )
else
{поиск элемента с заданным ключом}
if Elem < Tree^.Elem then DeleteElemOfTree( Tree^.Left, Elem )
else
if Elem > Tree^.Elem then
DeleteElemOfTree( Tree^.Right, Elem )
else begin
{элемент найден, необходимо его удалить}
ServiceVar1:= Tree;
{второй случай процедуры удаления}
if ServiceVar1^.Right= nil then
Tree:= ServiceVar1^.Left
else
if ServiceVar1^.Left= nil then
Tree:= ServiceVar1^.Right
else
{третий случай процедуры удаления}
Del( ServiceVar1^.Left )
end
end;
Вспомогательная рекурсивная процедура Del вызывается лишь в третьем случае процедуры удаления. Она переходит к самому правому элементу левого поддерева удаляемого элемента, а затем заменяет информационное поле удаляемого на значение поля найденного элемента.
Похожие работы
... ссылочного типа: <задание ссылочного типа>::= ^<имя типа> ^ - признак ссылочного типа; <имя типа> - имя стандартного либо описанного ранее типа. Это тип динамических объектов, которые может представлять переменная ссылочного типа. Надо подчеркнуть , что здесь может быть только имя типа. Сами переменные ссылочного типа вводятся обычным образом. type массив = array ...
... ячейка, а имя переменной превращается в адрес ячейки. Появление этого адреса происходит в результате работы специального оператора языка (NEW), однако его значение в большинстве случаев не используется при программировании на алгоритмических языках типа Паскаль. Условимся считать, что адрес ячейки, которая будет хранить переменную А, есть А. Или, другими словами, А - это общее имя переменной и ...
... Закрыть программу можно нажатием на кнопку «Закрыть» или F10. Заключение В квалификационной работе мы попытались раскрыть более полно и наглядно понятие линейного списка, однонаправленного и двунаправленного списков, стека, дека и очереди. Сформировать и закрепить познавательный интерес к данной теме у учащихся. Выявлять и развивать творческие способности в использовании полученного навыка при ...
... "nсреднее целое равно " << MidInt / double(NMax) << "n"; cout << "среднее вещественное равно: " << MidReal / n << "n"; fclose(t); } Списки Обсудим вопрос о том, как в динамической памяти можно создать структуру данных переменного размера. Разберем следующий пример. В процессе физического эксперимента многократно снимаются показания прибора (допустим, термометра) ...
0 комментариев