Содержание
1. Статистический формуляр исходных данных задания
2. Качественный анализ исходных данных
3. Изучение концентрации банковского капитала
4. Проверка однородности и нормальности распределения
5. Построение ряда распределения
6. Определение характеристик генеральной совокупности
7. Установка наличия и характера связи
8. Определение тесноты и существенности связи
9. Уравнение парной регрессии
10. Анализ динамики прибыли
11. Прогнозирование значения прибыли
Статистический формуляр исходных данных задания| Таблица №1 | ||||||
| № банка п/п | Капитал, млн. руб. | Прибыль, млн. руб. | ||||
| IV квартал отчетного года | IV квартал предыдущего года | Отчетный год | ||||
| I квартал | II квартал | III квартал | IV квартал | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 982 | 25,4 | 28,4 | 27,6 | 34,3 | 35,1 |
| 2 | 971 | 19,3 | 21,3 | 18,4 | 20,1 | 22,6 |
| 3 | 965 | 17,1 | 18,1 | 19,6 | 18,6 | 20,1 |
| 4 | 1045 | 18,4 | 18,2 | 20,3 | 19,1 | 20,8 |
| 5 | 1004 | 17,3 | 19,8 | 21,6 | 22,3 | 23,8 |
| 6 | 958 | 20,3 | 17,6 | 18,1 | 17,8 | 19,3 |
| 7 | 932 | 15,6 | 16,2 | 18,3 | 17,4 | 21,3 |
| 8 | 931 | 16,8 | 17,2 | 15,6 | 20,0 | 18,4 |
| 9 | 928 | 17,1 | 15,6 | 16,3 | 18,4 | 20,2 |
| 10 | 924 | 15,1 | 14,8 | 17,3 | 16,5 | 19,4 |
| 11 | 921 | 16,8 | 15,6 | 18,3 | 17,4 | 20,6 |
| 12 | 901 | 15,1 | 14,3 | 17,6 | 16,2 | 15,6 |
| 13 | 880 | 17,4 | 18,3 | 15,6 | 19,0 | 21,3 |
| 14 | 873 | 15,5 | 16,5 | 16,0 | 17,3 | 18,1 |
| 15 | 864 | 18,8 | 19,6 | 17,3 | 18,4 | 21,2 |
| 16 | 859 | 13,6 | 15,8 | 17,1 | 14,2 | 18,4 |
| 17 | 804 | 13,8 | 14,7 | 18,3 | 17,1 | 16,5 |
| 18 | 821 | 11,6 | 15,3 | 13,2 | 15,5 | 17,2 |
| 19 | 801 | 15,2 | 14,3 | 15,6 | 17,0 | 18,0 |
| 20 | 801 | 13,3 | 15,4 | 16,2 | 17,3 | 19,4 |
| 21 | 800 | 12,7 | 14,6 | 13,4 | 17,1 | 15,3 |
| 22 | 785 | 13,6 | 13,2 | 14,1 | 13,7 | 14,4 |
| 23 | 794 | 12,6 | 11,8 | 13,1 | 13,0 | 12,5 |
| 24 | 795 | 15,8 | 13,6 | 12,1 | 17,3 | 16,2 |
| 25 | 770 | 11,6 | 11,3 | 13,2 | 12,4 | 11,5 |
| 26 | 778 | 10,2 | 13,1 | 14,3 | 11,6 | 13,8 |
Целью качественного (теоретического) анализа исходных данных является установление факторного ![]() и результативного
и результативного ![]() показателей. Из таблицы №1 видно, что величина капитала в значительной степени определяет прибыль банка. Следовательно, капитал банка является факторным показателем
показателей. Из таблицы №1 видно, что величина капитала в значительной степени определяет прибыль банка. Следовательно, капитал банка является факторным показателем ![]() , а прибыль банка является результативным показателем
, а прибыль банка является результативным показателем ![]() .
.
Для изучения концентрации банковского капитала необходимо выполнить группировку по величине капитала, выделив мелкие, средние и крупные банки.
Для определения величины интервала, можно воспользоваться следующей формулой:
![]()
| где |
| максимальное значение факторного признака |
|
| минимальное значение факторного признака | |
|
| число групп |
По данным графы 2 таблицы №1 величина интервала:
![]()
Для заполнения таблицы №2 на основании данных из таблицы №1, нижнюю границу первого интервала принимаем равной минимальному значению факторного признака, а верхнюю границу каждого интервала получаем прибавлением к нижней границе величины интервала:
| Таблица №2 | |||
| № п/п | Группы по величине капитала, млн. руб. | Капитал, млн. руб. (IV квартал отчетного года) | Прибыль, млн. руб. (IV квартал отчетного года) |
| 1 | 2 | 3 | 4 |
| I | 770 – 862 | 859; 804; 821; 801; 801; 800; 785; 794; 795; 770; 778 | 18,4; 16,5; 17,2; 18,0; 19,4; 15,3; 14,4; 12,5; 16,2; 11,5; 13,8 |
| II | 862 – 954 | 932; 931; 928; 924; 921; 901; 880; 873; 864 | 21,3; 18,4; 20,2; 19,4; 20,6; 15,6; 21,3; 18,1; 21,2 |
| III | 954 – 1046 | 982; 971; 965; 1045; 1004; 958 | 35,1; 22,6; 20,1; 20,8; 23,8; 19,3 |
Результаты группировки приведены в групповой таблице №3, где значения показателей капитала и прибыли по каждой группе и по совокупности в целом получены суммированием соответствующих значений таблицы №2 по каждому банку.
Показатели капитала и прибыли в среднем на один банк по каждой группе и по совокупности в целом получены делением соответствующей суммарной величины на число банков по группе и по совокупности в целом.
Показатели удельного веса (долей) получены делением соответствующего показателя по группе на итог по совокупности в целом.
| Таблица №3 | |||||||||
| № п/п | Капитал, млн. руб. | Число банков | Капитал, млн. руб. | Прибыль, млн. руб. | Удельный вес, % | ||||
| Всего | В среднем на один банк | Всего | В среднем на один банк | по числу банков | по величине капитала | по величине прибыли | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| I | 770 – 862 | 11 |
|
|
|
|
|
|
|
| II | 862 – 954 | 9 |
|
|
|
|
|
|
|
| III | 954 – 1046 | 6 |
|
|
|
|
|
|
|
| Итого: |
|
|
|
|
|
|
|
| |
По результатам группировки, приведенной в таблице №3 можно сделать следующие выводы:
Основная часть банков принадлежит к группе мелких банков, их доля составляет 42,3%. В этой группе сосредоточена наибольшая часть капитала, составляющая 38,5% от общего объема капитала и ими получено 35,27% общей прибыли.
Наименьшее число относится к группе крупных банков, их доля составляет 23,1%. В этой группе сосредоточена наименьшая доля капитала, составляющая 25,9% от общего объема капитала, но ими получена прибыль, составляющая 28,86% от общего объема прибыли, что свидетельствует о более высокой эффективности их деятельности.
Значения капитала и прибыли в среднем на один банк существенно различаются по группам: в первой группе капитал составляет 800,7 млн. руб., прибыль 15,7 млн. руб.; во второй группе значение капитала в среднем на один банк составляет 906 млн. руб., что в 1,13 раза выше, чем в первой группе, прибыль составляет 19,6 млн. руб., что в 1,25 раза выше, чем в первой группе; в третьей группе показатели в среднем на один банк капитала и прибыли составляют 987,5 млн. руб. и 23,6 млн. руб. соответственно, что по капиталу превосходит аналогичный показатель первой группы в 1,23 раза и второй группы в 1,09 раза, по прибыли превосходит аналогичный показатель первой группы в 1,5 раза, а второй группы в 1,2 раза.Таким образом, сопоставление роста прибыли по группам и роста величины капитала, также свидетельствует о наибольшей эффективности банков третьей группы.
Проверка однородности и нормальности распределенияНеобходимой предпосылкой корректного использования статистических методов анализа является однородность совокупности. Неоднородность совокупности возникает вследствие значительной вариации значений признака или попадания в совокупность резко выделяющихся, так называемых “аномальных” наблюдений. Для их выявления используем правило трех сигм, которое состоит в том, что “аномальными” будут те банки, у которых значения анализируемого признака будут выходить за пределы интервала, т.е.:
![]()
| где |
| среднее значение факторного показателя |
|
| среднее квадратическое отклонение по факторному показателю | |
|
| значение факторного показателя |
Выделив и исключив “аномальные” банки, оценку однородности проведем по коэффициенту вариации, который должен быть не более 33,3%:
| где |
| коэффициент вариации |
|
| среднее значение факторного показателя | |
|
| среднее квадратическое отклонение по факторному показателю |
Для выявления “аномальных” наблюдений по первичным данным о величине капитала вычислим его среднюю величину и среднее квадратическое отклонение (См. таблицу №4):
| где |
| среднее значение факторного показателя |
|
| среднее квадратическое отклонение по факторному показателю | |
|
| значение факторного показателя | |
|
| число единиц в совокупности |
![]()
![]()
| Таблица №4 | ||||||||||||||
| № банка п/п | Капитал, млн. руб.
|
|
| Прибыль, млн. руб.
|
|
|
| |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||||||
| 1 | 982 |
|
| 35,1 |
|
|
| |||||||
| 2 | 971 |
|
| 22,6 |
|
|
| |||||||
| 3 | 965 |
|
| 20,1 |
|
|
| |||||||
| 4 | 1045 |
|
| 20,8 |
|
|
| |||||||
| 5 | 1004 |
|
| 23,8 |
|
|
| |||||||
| 6 | 958 |
|
| 19,3 |
|
|
| |||||||
| 7 | 932 |
|
| 21,3 |
|
|
| |||||||
| 8 | 931 |
|
| 18,4 |
|
|
| |||||||
| 9 | 928 |
|
| 20,2 |
|
|
| |||||||
| 10 | 924 |
|
| 19,4 |
|
|
| |||||||
| 11 | 921 |
|
| 20,6 |
|
|
| |||||||
| 12 | 901 |
|
| 15,6 |
|
|
| |||||||
| 13 | 880 |
|
| 21,3 |
|
|
| |||||||
| 14 | 873 |
|
| 18,1 |
|
|
| |||||||
| 15 | 864 |
|
| 21,2 |
|
|
| |||||||
| 16 | 859 |
|
| 18,4 |
|
|
| |||||||
| 17 | 804 |
|
| 16,5 |
|
|
| |||||||
| 18 | 821 |
|
| 17,2 |
|
|
| |||||||
| 19 | 801 |
|
| 18,0 |
|
|
| |||||||
| 20 | 801 |
|
| 19,4 |
|
|
| |||||||
| 21 | 800 |
|
| 15,3 |
|
|
| |||||||
| 22 | 785 |
|
| 14,4 |
|
|
| |||||||
| 23 | 794 |
|
| 12,5 |
|
|
| |||||||
| 24 | 795 |
|
| 16,2 |
|
|
| |||||||
| 25 | 770 |
|
| 11,5 |
|
|
| |||||||
| 26 | 778 |
|
| 13,8 |
|
|
| |||||||
| Итого: | ||||||||||||||
![]()
![]()
![]()
![]()
Поскольку минимальное значение капитала (770 млн. руб.) больше нижней границы интервала (643 млн. руб.), а максимальное значение (1045 млн. руб.) меньше верхней границы (1117 млн. руб.), то можно считать, что в данной совокупности “аномальных” наблюдений нет.
Проверка однородности осуществляется по коэффициенту вариации:
![]()
Т.к. ![]() , следовательно, данная совокупность однородна.
, следовательно, данная совокупность однородна.
Для построения ряда распределения необходимо определить число групп и величину интервала. Для определения числа групп воспользуемся формулой Стерджесса:
![]()
| где | m | число групп (всегда целое) |
|
| число единиц в совокупности |
Величину интервала определим по формуле:
![]()
| где |
| максимальное значение факторного признака |
|
| минимальное значение факторного признака | |
|
| число групп |
![]()
Нижнюю границу первого интервала принимаем равной минимальному значению факторного признака, а верхнюю границу каждого интервала получаем прибавлением к нижней границе величины интервала. По каждой группе подсчитываем число банков, за ![]() принимаем середину интервала, условно считая, что она будет равной средней по интервалу, и результаты заносим в таблицу №5:
принимаем середину интервала, условно считая, что она будет равной средней по интервалу, и результаты заносим в таблицу №5:
| Таблица №5 | |||||||||
| № п/п | Капитал, млн. руб. | Число банков |
|
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| I | 770 – 825 | 10 | |||||||
| II | 825 – 880 | 3 | |||||||
| III | 880 – 935 | 7 | |||||||
| IV | 935 – 990 | 4 | |||||||
| V | 990 – 1045 | 2 | |||||||
| Итого: | |||||||||
Среднюю по ряду распределения рассчитываем по средней арифметической взвешенной:
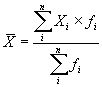
| где |
| средняя по ряду распределения |
|
| средняя по i-му интервалу | |
|
| частота i-го интервала (число банков в интервале) |
![]()
Мода – это наиболее часто встречающееся значение признака. Для интервального ряда мода определяется по формуле:
![]()
| где |
| значение моды |
|
| нижняя граница модального интервала | |
|
| величина модального интервала | |
|
| частота модального интервала | |
|
| частота интервала, предшествующего модальному | |
|
| частота послемодального интервала |
Модальный интервал определяется по наибольшей частоте. Для данного ряда наибольшее значение частоты равно 10, т.е. это будет интервал 770 – 825, тогда значение моды:
![]()
Медиана – значение признака, лежащее в середине ранжированного (упорядоченного) ряда распределения.
Номер медианы определяется по формуле:
![]()
| где |
| номер медианы |
|
| число единиц в совокупности |
![]()
т.к. медианы с дробным номером не бывает, то полученный результат указывает, что медиана находится посередине между 13-й и 14-й величинами совокупности.
Значение медианы можно определить по формуле:
![]()
| где |
| значение медианы |
|
| нижняя граница медианного интервала | |
|
| величина медиального интервала | |
|
| номер медианы | |
|
| накопленная частота интервала, предшествующего медианному | |
|
| частота медианного интервала |
По накопленной частоте ![]() определяем, что медиана будет находиться в интервале 880 – 935, тогда значение медианы:
определяем, что медиана будет находиться в интервале 880 – 935, тогда значение медианы:
![]()
Наряду со средними величинами большое значение имеет изучение отклонений от средних, при этом представляет интерес совокупность всех отклонений, т.к. от их размера и распределения зависит типичность и надежность средних характеристик. Наиболее простым из этих показателей является показатель размаха вариации, который рассчитывается по формуле:
![]()
| где |
| размах вариации |
|
| максимальное значение признака | |
|
| минимальное значение признака |
![]()
Размах вариации характеризует разброс только крайних значений, поэтому он не может быть достоверной характеристикой вариации признака. Распределение отклонений можно уловить, определив все отклонения от средней, для этого можно определить среднее арифметическое (линейное) отклонение, которое рассчитывается по формуле:
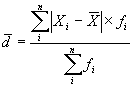
| где |
| среднее линейное отклонение |
|
| средняя по ряду распределения | |
|
| средняя по i-му интервалу | |
|
| частота i-го интервала (число банков в интервале) |
![]()
Среднее линейное отклонение, как меру вариации признака применяют крайне редко. Чаще отклонения от средней возводят в квадрат и из квадратов отклонений вычисляют среднюю величину. Полученная мера вариации называется дисперсией, а корень квадратный из дисперсии, есть среднее квадратическое отклонение, которое выражает абсолютную меру вариации и вычисляется по формуле:
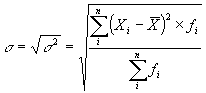
| где |
| среднее квадратическое отклонение |
|
| дисперсия | |
|
| средняя по ряду распределения | |
|
| средняя по i-му интервалу | |
|
| частота i-го интервала (число банков в интервале) |
![]()
По рассчитанным показателям достаточно трудно судить о степени вариации признака в совокупности, т.к. их величина зависит от размера значений признака, поэтому более объективной характеристикой будет коэффициент вариации, который рассчитывается по формуле:
![]()
| где |
| коэффициент вариации |
|
| среднее квадратическое отклонение | |
|
| средняя по ряду распределения |
![]()
Т.к. ![]() , следовательно, данное значение коэффициента вариации свидетельствует об однородности совокупности и надежности средней.
, следовательно, данное значение коэффициента вариации свидетельствует об однородности совокупности и надежности средней.
Для характеристики дифференциации банков по величине капитала, рассчитаем коэффициент фондовой дифференциации по формуле:
![]()
| где |
| коэффициент фондовой дифференциации |
|
| средняя из 10% максимальных значений признака | |
|
| средняя из 10% минимальных значений признака |
Т.к. 10% от 26 будет 2,6, то можно взять значения трех банков, имеющих самые большие и самые меньшие значения капитала:
|
|
|
Тогда:
|
|
|
![]()
Следовательно, средняя из 10% максимальных значений в 1,3 раза превышает среднюю из 10% минимальных значений.
Определение характеристик генеральной совокупностиПо условию задания предполагается, что исходные данные по 26 банкам являются 5% выборкой из некоторой генеральной совокупности. Для определения характеристик генеральной совокупности необходимо:
определить характеристики выборочной совокупности: среднюю величину; дисперсию; долю единиц, обладающих значением изучаемого признака; дисперсию доли; рассчитать ошибки выборки; распространить результаты выборки на генеральную совокупность путем определения доверительных интервалов, в которых с определенной вероятностью можно гарантировать нахождение характеристик генеральной совокупности.Для определения характеристик выборочной совокупности, воспользуемся результатами расчетов п.5 задания, в котором определили, что:
средняя величина капитала составляет: ![]()
дисперсия равна: ![]()
Доля банков, у которых капитал превышает среднюю величину, для выборочной совокупности определяется по первичным данным таблицы №1. Число таких банков равно 13, тогда их доля ![]() в выборочной совокупности составляет:
в выборочной совокупности составляет:
![]()
Дисперсия доли рассчитывается, как произведение значения доли на дополнение ее до единицы, т.е.: ![]() . Тогда, дисперсия доли составляет:
. Тогда, дисперсия доли составляет: ![]()
Для расчета ошибок выборки можно воспользоваться формулами для бесповторного отбора, т.к. из условия задания можно определить численность генеральной совокупности. Тогда, средняя ошибка выборки для средней величины:
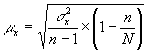
| где |
| дисперсия выборочной совокупности |
|
| численность единиц выборочной совокупности | |
|
| численность единиц генеральной совокупности |
Т.к. ![]() , что по условию составляет 5% от численности генеральной совокупности, то
, что по условию составляет 5% от численности генеральной совокупности, то ![]() , тогда средняя ошибка выборки для средней величины:
, тогда средняя ошибка выборки для средней величины:
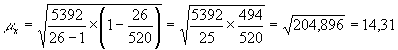
Предельная ошибка для средней величины рассчитывается по формуле:
![]()
| где |
| средняя ошибка выборки для средней величины |
|
| коэффициент доверия |
Коэффициент доверия ![]() принимается в зависимости от уровня доверительной вероятности и числа степеней свободы. Для малой выборки (меньше 30 единиц) определяется по таблице Стьюдента.
принимается в зависимости от уровня доверительной вероятности и числа степеней свободы. Для малой выборки (меньше 30 единиц) определяется по таблице Стьюдента.
При заданной вероятности ![]() и числа степеней свободы
и числа степеней свободы ![]()
![]() , табличное значение
, табличное значение ![]() . Тогда, предельная ошибка для средней величины:
. Тогда, предельная ошибка для средней величины:
![]()
Доверительный интервал для средней величины генеральной совокупности:
![]()
| где |
| средняя величина факторного признака выборочной совокупности |
|
| средняя величина факторного признака генеральной совокупности | |
|
| предельная ошибка средней величины факторного признака |
![]()
![]()
Следовательно, с вероятностью 0,95 можно гарантировать, что средняя величина капитала в расчете на один банк по генеральной совокупности будет находиться в пределах от ![]() до
до ![]()
Средняя ошибка выборки доли банков, у которых капитал превышает среднюю величину, для бесповторного отбора:
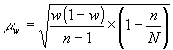
| где |
| дисперсия доли банков выборочной совокупности |
|
| численность единиц выборочной совокупности | |
|
| численность единиц генеральной совокупности |
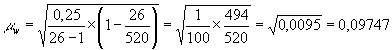
Предельная ошибка доли банков рассчитывается по формуле:
![]()
| где |
| средняя ошибка выборки доли банков |
|
| коэффициент доверия |
Коэффициент доверия ![]() при вероятности
при вероятности ![]() по таблице Стьюдента уже был определен, и он составляет
по таблице Стьюдента уже был определен, и он составляет ![]() . Тогда, предельная ошибка доли:
. Тогда, предельная ошибка доли:
![]()
Доверительный интервал для доли банков в генеральной совокупности:
![]()
| где |
| доля банков по выборочной совокупности |
|
| доля банков по генеральной совокупности | |
|
| предельная ошибка доли |
![]()
![]()
Следовательно, с вероятностью 0,95 можно гарантировать, что доля банков, у которых величина капитала больше среднего значения, по генеральной совокупности будет находиться в пределах от ![]() до
до ![]() .
.
Связь между факторными и результативными показателями может быть одной из двух видов: функциональной или корреляционной.
Функциональной, называется такая взаимосвязь, которая проявляется с одинаковой силой у всех единиц совокупности, независимо от изменения других признаков данного явления. Функциональные связи обычно выражаются формулами.
Корреляционной называется взаимосвязь между факторным и результативным показателем, которая проявляется только “в общем и среднем” при массовом наблюдении фактических данных.
Содержательный анализ исходных данных выполнен ранее и установлено, что капитал – факторный признак ![]() , прибыль – результативный
, прибыль – результативный ![]() , поэтому на основании проведенных ранее вычислений можно сделать однозначный вывод, что связь между факторным и результативным признаком не полная, а проявляется лишь в общем, среднем, т.е. речь может идти только о корреляционном виде связи.
, поэтому на основании проведенных ранее вычислений можно сделать однозначный вывод, что связь между факторным и результативным признаком не полная, а проявляется лишь в общем, среднем, т.е. речь может идти только о корреляционном виде связи.
Непременными условиями корректного использования корреляционного метода являются достаточно большое число единиц совокупности, однородность совокупности и отсутствие выделяющихся, “аномальных” наблюдений, проверка которых уже выполнена в п.4 данного задания.
Для установки факта наличия связи, заполним групповую таблицу №5а, по данным таблицы №5; на рисунке №1 построим поле корреляции, по исходным данным таблицы №1, и эмпирическую линию регрессии, по данным таблицы №5а, принимая середину интервала за ![]() , за
, за ![]() – прибыль в среднем на один банк:
– прибыль в среднем на один банк:
| Таблица №5а | ||||
| № п/п | Капитал, млн. руб. | Число Банков | Середина интервала, млн. руб. | Прибыль в среднем на один банк, млн. руб. |
| 1 | 2 | 3 | 4 | 5 |
| I | 770 – 825 | 10 | 797,5 | 15,48 |
| II | 825 – 880 | 3 | 852,5 | 19,23 |
| III | 880 – 935 | 7 | 907,5 | 19,54 |
| IV | 935 – 990 | 4 | 962,5 | 24,27 |
| V | 990 – 1045 | 2 | 1017,5 | 22,30 |
Анализ таблицы №5а свидетельствует, что существует зависимость между капиталом и прибылью банков.
Поле корреляции, имеет форму вытянутого эллипса и ясно показывает, что имеется тенденция к росту из левого нижнего угла в правый верхний. Значит, имеется прямая корреляционная зависимость между капиталом и прибылью банков.
Эмпирическая линия регрессии также имеет некоторую тенденцию к росту, что также свидетельствует о наличии прямой корреляционной зависимости между капиталом и прибылью банков.
Определение тесноты и существенности связиЭмпирическая линия регрессии (рисунок №1) – ломаная линия. Изломы этой линии свидетельствуют о влиянии на признак ![]() прочих факторов, помимо признака
прочих факторов, помимо признака ![]() . Чтобы абстрагироваться от влияния прочих факторов, нужно прибегнуть к выравниванию полученной ломаной линии регрессии. Для этого сначала необходимо установить теоретическую форму связи, т.е. выбрать определенный вид функции, наилучшим образом отображающий характер изучаемой связи.
. Чтобы абстрагироваться от влияния прочих факторов, нужно прибегнуть к выравниванию полученной ломаной линии регрессии. Для этого сначала необходимо установить теоретическую форму связи, т.е. выбрать определенный вид функции, наилучшим образом отображающий характер изучаемой связи.
Выбор формы связи имеет решающее значение в корреляционно-регрессионном анализе, но этот выбор всегда связан с некоторой условностью, вызванный тем, что нужно находить форму функциональной зависимости, в то время как зависимость лишь в той или иной степени приближается к функциональной. Но если зависимость довольно высокая, т.е. довольно близко приближается к функциональной, тогда именно теоретическая линия регрессии и ее параметры приобретают практическое значение.
На основании качественного анализа исходных данных (таблица №1) и эмпирической линии регрессии (рисунок №1) можно предположить, что между капиталом и прибылью банков существует линейная зависимость. Для определения тесноты этой зависимости воспользуемся линейным коэффициентом корреляции:
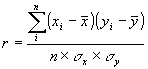
| где |
| значение факторного показателя |
|
| среднее значение факторного показателя | |
|
| значение результативного показателя | |
|
| среднее значение результативного показателя | |
|
| число единиц в совокупности | |
|
| среднее квадратическое отклонение по факторному показателю | |
|
| среднее квадратическое отклонение по результативному показателю |
Для вычисления линейного коэффициента корреляции воспользуемся расчетами, выполненными в таблице №4, тогда
![]()
![]()
Среднее значение и среднее квадратическое отклонение результативного показателя рассчитывается аналогично факторному:
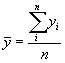
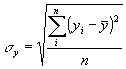
| где |
| среднее значение результативного показателя |
|
| среднее квадратическое отклонение по результативному показателю | |
|
| значение результативного показателя | |
|
| число единиц в совокупности |
![]()
![]()
![]()
Коэффициент корреляции показывает не только тесноту, но и направление связи. Его значение изменяется от ![]() до
до ![]() . Если коэффициент имеет знак минус, значит, связь обратная, если имеет знак плюс, то связь прямая. Близость к единице в том и в другом случае характеризует близость к функциональной зависимости.
. Если коэффициент имеет знак минус, значит, связь обратная, если имеет знак плюс, то связь прямая. Близость к единице в том и в другом случае характеризует близость к функциональной зависимости.
Таким образом, значение ![]() свидетельствует о прямой и достаточно тесной связи между величиной капитала и прибылью банка.
свидетельствует о прямой и достаточно тесной связи между величиной капитала и прибылью банка.
Однако, чтобы это утверждать, необходимо дать оценку существенности линейного коэффициента корреляции, что можно выполнить на основании расчета t-критерия Стьюдента:
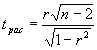
| где |
| линейный коэффициент корреляции |
|
| число единиц в совокупности |
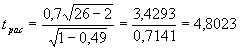
Для числа степеней свободы ![]() и уровня значимости 1% табличное значение
и уровня значимости 1% табличное значение ![]() , т.е.
, т.е. ![]() . Следовательно, с вероятностью
. Следовательно, с вероятностью ![]() можно утверждать, что в генеральной совокупности существует достаточно тесная прямо пропорциональная линейная зависимость между величиной капитала и прибылью банка.
можно утверждать, что в генеральной совокупности существует достаточно тесная прямо пропорциональная линейная зависимость между величиной капитала и прибылью банка.
Для выравнивания эмпирической линии регрессии (рисунок №1) необходимо найти теоретическое уравнение связи. На основании вычислений, произведенных в п.8, выравнивание можно производить по прямой, т.е. теоретическое уравнение связи, имеющее линейный характер, в общем виде будет иметь вид:
![]()
Найти теоретическое уравнение связи – значит, в данном случае, определить параметры прямой. Это можно сделать способом наименьших квадратов, который дает систему нормальных уравнений для нахождения параметров прямой:
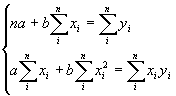
| где |
| значение факторного показателя |
|
| значение результативного показателя | |
|
| число единиц в совокупности |
| Тогда: |
|
|
| где |
| коэффициент корреляции |
|
| среднее квадратическое отклонение по факторному показателю | |
|
| среднее квадратическое отклонение по результативному показателю | |
|
| среднее значение результативного показателя | |
|
| среднее значение факторного показателя |
![]()
![]()
Следовательно, теоретическое уравнение связи имеет вид (см. рисунок №1):
![]()
С экономической точки зрения коэффициент регрессии ![]() говорит о том, что при увеличении капитала на
говорит о том, что при увеличении капитала на ![]() прибыль возрастает на
прибыль возрастает на ![]() или на
или на ![]()
По коэффициенту регрессии можно вычислить коэффициент эластичности и ![]() - коэффициент.
- коэффициент.
Коэффициент эластичности показывает, на сколько процентов увеличится результативный показатель при увеличении факторного признака на 1%:
![]()
| где |
| среднее значение результативного показателя |
|
| среднее значение факторного показателя |
![]()
Следовательно, при увеличении капитала на 1%, прибыль увеличивается на 1,82%.
![]() - коэффициент показывает, на сколько своих среднеквадратических отклонений измениться результативный показатель при изменении факторного признака на одно свое среднеквадратическое отклонение:
- коэффициент показывает, на сколько своих среднеквадратических отклонений измениться результативный показатель при изменении факторного признака на одно свое среднеквадратическое отклонение:
![]()
| где |
| среднеквадратическое отклонение по факторному показателю |
|
| среднеквадратическое отклонение по результативному показателю |
![]()
Следовательно, при увеличении капитала на одно свое среднеквадратическое отклонение прибыль увеличивается на 0,7 своих среднеквадратических отклонений.
Анализ динамики прибыли Анализ динамики выполняется путем расчета: показателей, характеризующих изменение анализируемого показателя по периодам; средних показателей динамики.Показатели, характеризующие изменение анализируемого показателя по периодам, могут быть рассчитаны ценным и базисным методом. Ценные показатели динамики характеризуют изменение каждого последующего показателя по сравнению с предыдущим, а базисные по сравнению с уровнем, принятым за базу сравнения. К таким показателям относятся:
Абсолютный прирост:
|
|
|
| где |
| уровень сравниваемого периода |
|
| уровень предыдущего периода | |
|
| уровень базисного периода |
Темп роста:
|
|
|
| где |
| уровень сравниваемого периода |
|
| уровень предыдущего периода | |
|
| уровень базисного периода |
Темп прироста:
|
|
|
| где |
| ценной темп роста сравниваемого периода |
|
| базисный темп роста сравниваемого периода |
Абсолютное значение одного процента прироста:
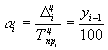
| где |
| ценной абсолютный прирост сравниваемого периода |
|
| ценной темп прироста сравниваемого периода | |
|
| уровень предыдущего периода |
Пункты роста:
![]()
| где |
| базисный темп роста сравниваемого периода |
|
| базисный темп роста предыдущего периода |
К средним показателям динамики относятся:
Средний уровень ряда:
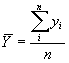
| где |
| уровень периода |
|
| число уровней ряда динамики в изучаемом периоде |
Средний абсолютный прирост:
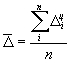
| где |
| ценной абсолютный прирост периода |
|
| число годовых абсолютных приростов |
Средний коэффициент роста:
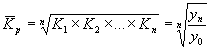
| где |
| последний уровень ряда динамики в изучаемом периоде |
|
| уровень базисного периода | |
|
| число уровней ряда динамики в изучаемом периоде |
Средний темп роста:
![]()
| где |
| средний коэффициент роста |
Средний темп прироста:
![]()
| где |
| средний коэффициент роста |
Для выполнения анализа динамики, из таблицы №1 по данным о прибыли банка №1 за отчетный год (4 квартала), рассчитаем все приведенные выше показатели динамики, при этом за уровень базисного периода примем показатель прибыли за IV квартал предыдущего года. Результаты вычислений показателей, характеризующих изменение прибыли банка по периодам отражены в таблице №6:
| Таблица №6 | |||||||||
| Период времени | Прибыль, млн. руб. | Абсолютный прирост, млн. руб. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста | Пункты роста, % | |||
| Ценной | Базисный | Ценной | Базисный | Ценной | Базисный | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| IV кв. предыдущего года | 25,4 | — | — | — | — | — | — | — | — |
| I кв. | 28,4 |
|
|
|
|
|
|
| — |
| II кв. | 27,6 |
|
|
|
|
|
|
|
|
| III кв. | 34,3 |
|
|
|
|
|
|
|
|
| IV кв. | 35,1 |
|
|
|
|
|
|
|
|
Т.к. изучаемым периодом является отчетный год, то средний уровень ряда:
![]()
Средний абсолютный прирост за отчетный год:
![]()
Средний темп роста прибыли за отчетный год:
![]()
Средний темп прироста прибыли за отчетный год:
![]()
Таким образом, средняя квартальная величина прибыли банка за отчетный год составила ![]() , а ее среднеквартальный абсолютный прирост составил
, а ее среднеквартальный абсолютный прирост составил ![]() , что соответствует среднеквартальному темпу роста
, что соответствует среднеквартальному темпу роста ![]() , и среднеквартальному темпу прироста
, и среднеквартальному темпу прироста ![]() .
.
Показатели динамики свидетельствуют о ежеквартальном росте прибыли, кроме II квартала отчетного года, когда было допущено снижение на ![]() , что составило
, что составило ![]() . В целом за отчетный год прибыль банка возросла на
. В целом за отчетный год прибыль банка возросла на ![]() , что составило
, что составило ![]() .
.
Найти прогнозное значение прибыли на следующий период, т.е. I квартал следующего года, можно использовать метод аналитического выравнивания по прямой. Для этого необходимо найти уравнение тренда, вида:
![]()
| где |
| порядковый номер периодов времени |
Чтобы найти уравнение тренда, нужно определить параметры ![]() и
и ![]() . Это можно сделать способом наименьших квадратов, который дает систему нормальных уравнений прямой:
. Это можно сделать способом наименьших квадратов, который дает систему нормальных уравнений прямой:
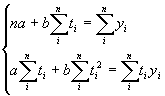
| где |
| значение прибыли банка за период |
|
| номер периода | |
|
| число периодов |
Нахождение параметров упрощается при использовании метода отсчета от условного нуля, тогда ![]() и система уравнений принимает вид:
и система уравнений принимает вид:
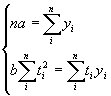
| Тогда: |
|
|
Для нахождения прогнозного значения прибыли банка №1 из таблицы №1, рассчитаем параметры уравнения тренда по результатам вычислений, произведенных в таблице №7:
|
|
|
Тогда, уравнение тренда, для расчета теоретического значения прибыли, имеет вид:
![]()
| Таблица №7 | |||||||
| Период времени | Прибыль, млн. руб.
| Условное обозначение периодов, |
|
| Теоретические (расчетные) значения прибыли, млн. руб. |
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| IV кв. предыдущего года | 25,4 | -2 | |||||
| I кв. | 28,4 | -1 | |||||
| II кв. | 27,6 | 0 | |||||
| III кв. | 34,3 | 1 | |||||
| IV кв. | 35,1 | 2 | |||||
| Итого | |||||||
Для нахождения прогнозного значения прибыли на I квартал следующего года, необходимо в уравнение тренда подставить соответствующее значение ![]() :
:
![]()
Этот прогноз называется точечным, и фактическое значение всегда будет сколько-нибудь отличаться от этой величины, поэтому необходимо найти доверительные интервалы прогноза:
![]()
| где |
| значение точечного прогноза |
|
| табличное значение | |
|
| среднее квадратическое отклонение от тренда | |
|
| число уровней ряда |
Среднее квадратическое отклонение от тренда рассчитывается по формуле:
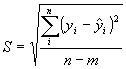
| где |
| фактическое значение уровня динамического ряда |
|
| расчетное значение уровня динамического ряда | |
|
| число уровней ряда | |
|
| число параметров в уравнении тренда (для прямой |
![]()
Определить относительную ошибку уравнения можно как коэффициент вариации по формуле:
![]()
| где |
| среднее квадратическое отклонение от тренда |
|
| среднее значение динамического ряда |
![]()
Следовательно, ошибка невелика и составляет ![]() .
.
По таблице Стьюдента, при уровне значимости 5% и числе степеней свободы ![]() , значение
, значение ![]() . Тогда доверительный интервал:
. Тогда доверительный интервал:
![]()
![]()
![]()
С вероятностью ![]() можно утверждать, что прибыль банка №1 в I квартале следующего года будет находиться в пределах от
можно утверждать, что прибыль банка №1 в I квартале следующего года будет находиться в пределах от ![]() до
до ![]()
Похожие работы
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... распределения генеральной совокупности F(x) и – эмпирической функция распределения Fn(x) , построенной по выборке х1,…,хn, называется функция. Теорема. Если F(x) непрерывна, то распределения статистики Колмогорова Dn не зависит от F(x). Условные математические ожидания и условные распределения. Св-ва условных мат. ожиданий. Аналоги формул полной вероятности и формулы Байеса для мат. ожиданий ГММЕ ...
... дает возможность статистического моделирования, происходящих в населении процессов. Потребность в моделировании возникает в случае невозможности исследования самого объекта. Наибольшее число моделей, применяемых в статистике населения, разработано для характеристики его динамики. Среди них выделяются экспоненциальные и логистические. Особое значение в прогнозе населения на будущие периоды имеют ...
... на задний план традиционными постановками. Несколько лет назад при описании современного этапа развития статистических методов нами были выделены [29] пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика, робастность, бутстреп, интервальная статистика, статистика объектов нечисловой природы. Обсудим их. 5. ...
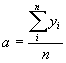
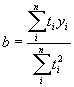










0 комментариев