Навигация
По методу наименьших квадратов произведем расчет коэффициентов уравнения регрессии из системы уравнении
2. По методу наименьших квадратов произведем расчет коэффициентов уравнения регрессии из системы уравнении
sum(Yi)= n*A + B sum(Xi)
sum(XiYi) = A* sum(Xi) + B*sum(Xi2))
имеем
А = sum(Yi) * sum(Xi2) - sum(XiYi) * sum(Xi)
n* sum(Xi2)- (sum(Xi) 2)
B = n*sum(XiYi) - sum(Xi)* sum(Yi)
n*sum(Xi2)- (sum(Xi))2
A=S2*S3-S4*S1 B=n*S4-S1*S2,
n*S3-S1*S1 n*S3-S1*S1
где S1=SUM(Xi) S2=SUM(Yi) S3=SUM(Xi2)
S4=SUM(XiYi)
n - общее число замеров, в нашем случае это 10
2.В результате расчета получено уравнение регрессии:
Y=8,917+0,583*Х
3.Подставив значения X в уравнение найдем Y расчетное.
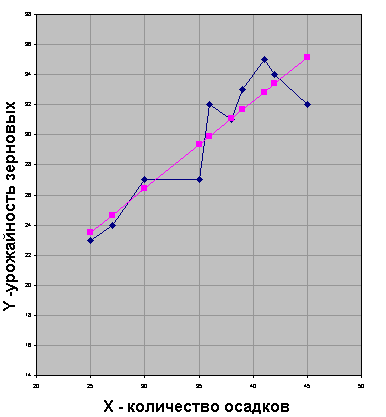
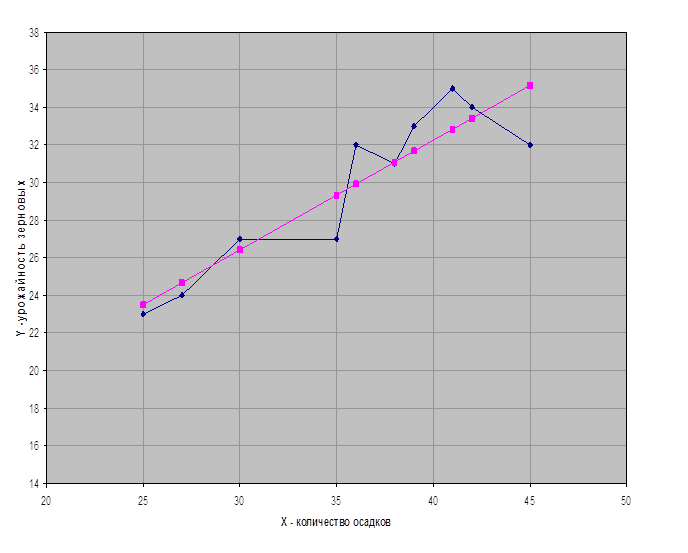
4.По значениям экспериментальным и теоретическим строим графики.
5. Связь между двумя случайными величинами, которая определяется с некоторой вероятностью, называется корреляционной. Для количественной оценки линейной корреляции используется коэффициент парной корреляции
r = 10*S4-S1*S2
(10*S3-S12)*(10*S5-S22)
S5=SUM(Yi2)
r=0,9104
По таблице Чеддока найдём тесноту связи между двумя явлениями, связь очень тесная"
6.Качество уравнений регрессии оценивают по его прогнозирующей способности. Уравнения хорошо прогнозируют(т.е. адекватно описывают) экспериментальные данные, если расхождения между экспериментальными и расчетными данными находятся в допустимых пределах.
Для проверки адекватности уравнения найдем среднюю относительную ошибку прогнозирования E:
E=100 *SUM |Yэi - Ypi|
10 Yэi
где Yэi -экспериментальное, Ypi - расчетное значение
Е=4,434%
Это сравнительно большое значение ошибки прогнозирования при полученном выше значении r.
Внимательно посмотрим на значения отклонений между фактическими и расчетными значениями Y. Почти непрерывный рост уражайности после 8 года сменяется спадом. 10 год дает самый большой прирост ошибки прогнозирования.
По всей видимости, для описания зависимости, лучше подошло бы не уравнение прямой, а уравнение параболлы, так как после достиженияопределенного уровня осадков урожайность начинает падать (много воды -это тоже плохо для урожая) см. последние значения Х и Y
В 4 год также сравнительно большое расхождение, это может бытьвызванно тем, что урожайность зерновых зависит не только от количества осадков, но и от многих других факторов, например от количества теплых дней. Просто было холодно.
| i | X | Y | X2 | XY | Yрасч | Y2 | (Y-Yрасч) Y |
| 1 | 25 | 23 | 625 | 575 | 23,5 | 529 | 0,0217 |
| 2 | 27 | 24 | 729 | 648 | 24,67 | 576 | 0,0279 |
| 3 | 30 | 27 | 900 | 810 | 26,42 | 729 | 0,0215 |
| 4 | 35 | 27 | 1225 | 945 | 29,33 | 729 | 0,0863 |
| 5 | 36 | 32 | 1296 | 1152 | 29,92 | 1024 | 0,0650 |
| 6 | 38 | 31 | 1444 | 1178 | 31,08 | 961 | 0,0026 |
| 7 | 39 | 33 | 1521 | 1287 | 31,67 | 1089 | 0,0403 |
| 8 | 41 | 35 | 1681 | 1435 | 32,83 | 1225 | 0,0620 |
| 9 | 42 | 34 | 1764 | 1428 | 33,42 | 1156 | 0,0171 |
| 10 | 45 | 32 | 2025 | 1440 | 35,17 | 1024 | 0,0991 |
| е | 358 | 298 | 13210 | 10898 | 298 | 9042 | 0,4434 |
| среднее | 35,8 | 29,8 |
Коэффициенты регрессии:
B=0,583
A=8,917
Уравнение регрессии: Y=8,917+0,583*Х
Коэффициент парной корреляции:
R=0,91
Средняя относительная ошибка прогнозирования:
E=4,43439
 ЗАДАЧА №4
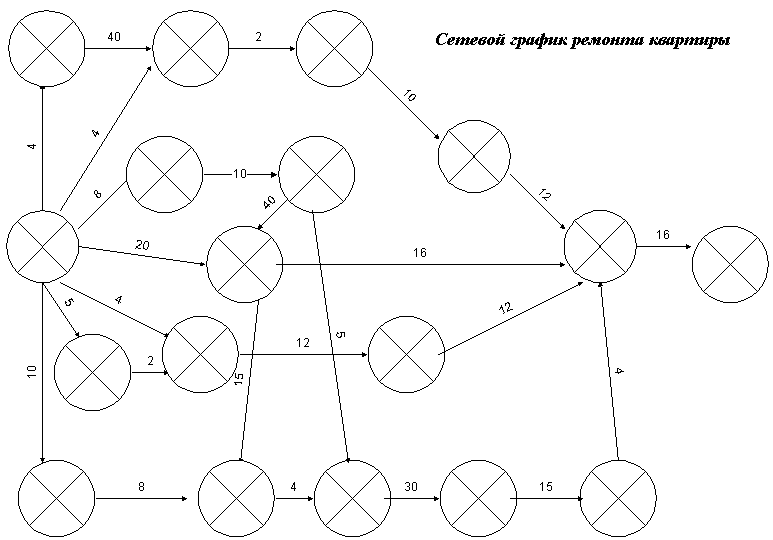
ЗАДАЧА №4 Построить сетевую модель ремонта Вашей квартиры
а) определить критический путь
б) рассчитать поздние сроки окончания и начала событий
в) рассчитать ранние сроки окончания и начала событий
г) рассчитать резервы событий
Решение:
Делаем ремонт двухкомнатной квартиры улучшенной планировки: жилая комната, детская, кухня, ванна, туалет и коридор.2. Необходимо сделать:
сменить обои во всех помещениях; покрасить окна; в зале и коридоре сделать подвесные потолки с рассеяным светом в оттальных помещениях потолок покрывается краской КЧ покрасить входную дверь; постелить по всей квартире линолиум3. Строим таблицу ремонта и сетевой график
4."Четырехсекторным" методом рассчитываем параметры сетевого графика и определяем "критический путь".
5. Расчитываем параметры сетевого графика и резервы времени
Похожие работы
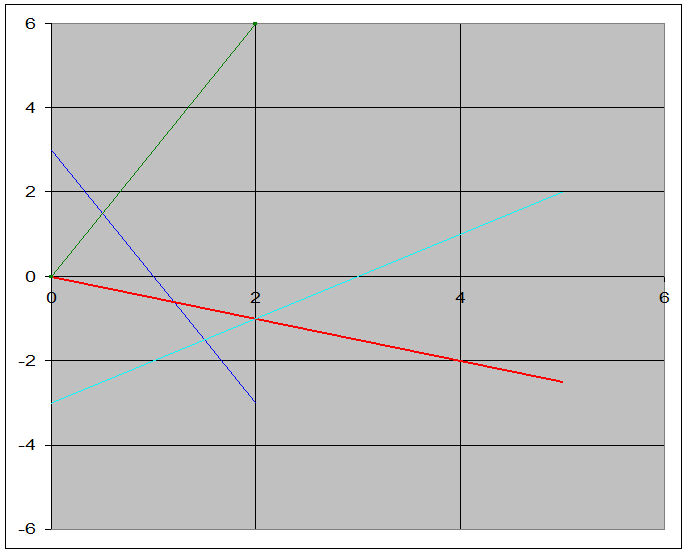
... модель задачи; б) поясните смысл целевой функции и ограничении Решение: а) Математическая модель 2x1+3x2 ...
... свойство pеализуется, возникает большое pазнообpазие моделей, а вместе с ним и пpоблема классификации моделей. II. Классификация моделей и виды моделиpования. ----------------------------------------------- В литеpатуpe, посвященной философским аспектам моделиpования пpедставлены pазличные классификационные пpизнаки, по котоpым выде- лены pазличные типы моделей. Остановимся на некотоpых из них. ...
в системах pаз цессов.Обсуждаются pазличные опpеделения понятия "инфоpмация", свя сами, pазличные интеpпpетации этого понятия (в физике, теp намике, химии и т.д.).Пpиводится обобщенная систематизация инфоpмационных пpоцессов (из меpение, экспеpиментальные исследования, пеpедача сообщений по каналам связи, моделиpование, умозаключение), об лучения.1.2. Введение в теоpию инфоpмацииВводится понятие ...
... и использования специалистов-пpофессионалов по анализу ваpиантов пpинимаемых pешений; pазpаботки и пpактического использования специальных методов анализа и сpавнения сложных альтеpнатив, возникающих в пpоцессе выбоpа. 3.ОБЩИЕ ПОДОХДЫ И РАЦИОHАЛЬHЫЕ ПРОЦЕДУРЫ В ПРОБЛЕМАХ ВЫБОРА В последние 20-30 лет появились подходы, pассматpиваемые многими как унивеpсальное сpедство pешения всех ...


0 комментариев