Навигация
Доходность купли-продажи финансовых инструментов. [5]
3. Доходность купли-продажи финансовых инструментов. [5]
Краткосрочные финансовые инструменты , такие как векселя, тратты, депозитные сертификаты, могут быть проданы до наступления срока их оплаты, что может приносить доход или убыток.
3. 1. Покупка и продажа векселя.
Эффективность от операции с векселями можно измерить в виде простых и сложных процентов. Результат операции зависит от разности цен купли-продажи, что определяется сроками этих актов до погашения векселя и уровнем учетных ставок.
Если номинал векселя Sрублей, учетная ставка d1, покупка, или учет, состоялась за д1 дней до наступления срока, то цена в момент покупки составила:
Р1 = S( 1- д1* d1/К), где К –временная база учета.
Продажа была осуществлена за д2 до погашения с дисконтированием по ставке d2
Р2 = S( 1- д2* d2/К)
Для простой ставки iэп получим следующее балансовое уравнение:
7) Р1( 1+ (д1- д2 )*iэп/К) = Р2
8) Þ iэп =( (Р2 - Р1)/ Р1)*К/( д1- д2)
Для того, чтобы операция не была убыточной, необходимо , чтобы :
д2* d2< д1* d1 или Р1 < Р2.
Если используется сложная ставка процента, то, при К=365, на основе балансового уравнения Р1( 1+iэ) (д1- д2 )/365= Р2,
получим iэ = (Р2 /Р1) 365/ (д1- д2 )-1
Þоперация доходна, пока d2< д1 /д2* d1.
Пример №5:Вексель куплен за 175 дней до его погашения, учетная ставка – 5%. Через 42 дня его реализовали по учетной ставке 4,67%. Эффективность, выраженная в виде простой годовой ставки процентов(временная база учета =360, наращения = 365), составит:
iэп = (((1-133*0,0467/360)/(1-175*0,05/360))-1)*365/42= 0,0628.
Эффективность операции, измеренная в виде эквивалентной ставки сложных процентов, равна:
iэ= (1+42*0,0628/365)365/42-1=0,0646.
Для того, чтобы операция купли-продажи принесла некоторый доход, учетная ставка d2 должна быть меньше, чем:
175*0,05/133=0,0658.
5
3. 2. Операции с финансовыми инструментами, приносящими простые проценты.
Финансовая эффективность сделок с депозитными сертификатами и другими краткосрочными финансовыми инструментами зависит от сроков актов купли-продажи до погашения, цен или процентных ставок, существующих на денежном рынке в момент совершения операции.
Наиболее распространенным видом депозитного сертификата является сертификат с разовой выплатой процентов. Возможны следующие варианты совершения операции по срокам:
1-покупается по номиналу, продается за д2 дней до погашения,
2-покупается после выпуска и погашается в конце срока,
3-покупается и продается в пределах объявленного срока.
1) Р1( 1+ (д1- д2 )*iэп/К) = Р2,
Здесь: Р1-номинал, Р2-цена продажи, д1, д2-сроки до погашения.
Если в качестве исходных параметров берутся процентные ставки i1 и i2(объявленная ставка сертификата и ставка рынка в момент продажи),то:
iэп = (((1+ д1* i1/К)/ (1+ д2* i2/К))-1)* К/(д1- д2 )
Если расчет основан на уровнях процентных ставок, то:
iэ=((К+ д1* i1) /( К+ д2* i2))365/(д1- д2 )-1.
Þв данном случае, инвестор получит доход только, если:
i2< д1* i1 / д2.
2) Р2(1+ д2* iэп/К) = Р1(1+ д1* i/К), где Р1-номинал, Р2-цена приобретения,i – объявленная процентная ставка. (см. рис. 4 в конце)
Из приведенного равенства получим значение iэп при заданной величине Р2:
iэп = (Р1 (1+ д1* i1/К)/ Р2-1)*К/ д2
Если в качестве измерителя эффективности принята ставка сложных процентов, то :
iэ=(Р1 (1+ д1* i/К)/ Р2)365/ д2-1
3) В данном варианте покупка производится спустя некоторое время после выпуска сертификата, а его продажа – до момента погашения.
На результат здесь влияют как срок владения инструментом, так и колебания процентных ставок.
Пример[6] №6:Сертификат был куплен за 140 дней до его выкупа за 1300 тыс. рублей. Инструмент был продан за 1400 тыс. рублей через 80 дней. Какова доходность операции, измеренная в виде простой и сложной ставок?
К = 365,
iэп=(1400-1300)/1300*(365/80)=0,351, т. е. 35,1%
Эквивалентная сложная ставка равна:
iэ=(1+80*0,351/365)365/80 –1=0,402, т. е. 40,2%
Величину i можно определить и непосредственно по формуле:
iэ=(1400/1300)365/80-1=0,402.
6
Пример№7:Сертификат с номиналом 230 тыс. рублей с объявленной доходностью 11%годовых ( в виде простых процентов) сроком 750 дней
куплен за 250 тыс. рублей за 260 дней до его оплаты. Какова доходность инвестиций в виде iэ?
Если временная база К=360 дней, то по формуле получим:
iэ=(230/250(1+(750*0,11/360)))365/260-1=0,1884 т. е. 18,84%.
4. Доходность потребительского кредита. [7]
Одной из распространенных форм кредитования являются потребительские кредиты – это краткосрочные ссуды, проценты на которые начисляются один раз на весь капитали за полный срок а выплаты производятся равными долями(постоянная р-срочная рента).
Реальная доходность такого вида ссуды в виде годовой ставки сложных процентов на инвестированные в операцию средства должна определяться с учетом фактического остатка задолженности после каждого платежа по кредиту. Таким образом, оценка искомойставки сводится к расчету коэффициента приведения такой ренты по данным, характеризующим условия потребительского кредита. Затем, на основе полученного коэффициента приведения рассчитывается искомая ставка.
Должник каждый раз в счет погашения выплачивает сумму
Y=D(1+ni)/рn.
Годовая сумма платежей равна:
Yр= D(1+ni)/n
Приравняем современную величину платежей (дисконтируя по неизвестной ставке iэ) сумме долга:
D= Yрa(р)n;iэ
Þa(р)n;iэ=n/(1+ni), где i – ставка простого процнта, принятого при расчете задолженности по потребительскому кредиту.
Рассчитанная ставка годовых сложных процентов заметно больше ставки, примененной при кредитовании.
Доходность потребительского кредита в виде годовой ставки сложных процентов:
| Годовая ставка за кредит | |||
| Число лет кредита | 4 | 5 | 8 |
| 3 | 7,8 | 9,7 | 15,6 |
| 4 | 7,6 | 9,5 | 15,4 |
| 5 | 7,5 | 9,2 | 15,1 |
Пример№8:Потребительский кредит выдан на 4 года на сумму 15 тысяч рублей по ставке 11% годовых. Общая сумма задолженности составит
15 000(1+4*0,11)=21 600
Погасительные платежи образуют постоянную ренту, коэффициент приведения которой:
7
а(12)4;iэ=4/1,44=2,7778
Найдем по формуле интерполяции приближенное значение ставки сложных процентов:
i = iн + (а-ан)/(ав-ан)*(iв-iн)
ан=2,588734568; ав=2,854978363
Þ0,15 +(2,7778-2,588734568)/( 2,854978363-2,588734568)*(0,2-0,15)=0,1855, т. е. 18,55%.
5 Долгосрочные ссуды. [8] 5. 1Ссуды с периодической выплатой процентов.Пусть ссуда D погашается через n-лет, проценты по простой процентной ставке i выплачиваются регулярно в конце года
Проценты в таком случае равны Di. Должнику с учетом комиссионных выдается ссуда в размере D (1-g). Балансовое уравнение, полученное дисконтированием всех платежей по неизвестной ставке iэ, имеет вид
D(1-g) – (DiSvj +Dvn)=0 , Snj=1
Здесь v=(1+iэ)-1, Svj= an;iэ
Это уравнение можно представить в виде функции от iэ следующим образом:
f(iэ)= vn+ian;iэ-(1-g)=0
Если проценты выплачиваются р-раз в году, то
f(iэ)= vn+(i/р)a(р)n;iэ-(1-g)=0
Пример№9:На три года выдана ссуда в 1млн. рублей под 10%годовых, проценты выплачиваются ежегодно. При выдаче ссуды сделана скидка в пользу владельца денег в размере 5%. В результате должник получил950000. Для расчета искомой ставки iэ сразу можно написать функцию:
f(iэ)=(1+iэ)-3-0,1* a3;iэ-0,95=0
Решение, например методом Ньютона-Рафсона или простым подбором, дает iэ = 1,12088. Таким образом, доходность операции для кредитора и соответственно цена кредита для должника в виде годовой ставки сложных процентов равны 12,088%.
Проверка:долг в размере950000 вырастет за первый год до 950*1,12088=1064,84, после первой уплаты задолженность составит 964,68; на конец второго года имеем 964,849*1,12088-100=981,47 и , наконец, в последнем году сумма, подлежащая уплате, равна 981,47*1,12088=110тыс. рублей.
5. 2 Ссуды с периодическими расходами по долгу.Допустим, что по ссуде периодически выплачиваются проценты и погашается основной долг, причем сумма расходов постоянна. Тогда балансовое уравнение для случая, когда платежи производятся в конце года, можно представить в виде:
D(1-g)-Ran;iэ =0, где R-срочная уплата.
Т. к. R=D/ an;i, то f(iэ)=an;iэ -an;i(1-g)=0
Если платежи осуществляются р-раз в году, то: f(iэ)=a(р)n;iэ -a(р)n;i(1-g)=0
,где a(р)n;iэ ,a(р)n;i-коэффициенты приведения годовой р-срочной ренты, члены которой равны расходам должника по ссуде.
Пример№10: Пусть в примере 9 задолженность погашается равными платежами. Все остальные условия не изменяются, тогда:
a3;iэ=a3;10(1-0,05)-2,48685*0,95=2,36251.
Расчет iэ по заданному значению можно легко осуществить с помощью линейной интерполяции. Т. к. iэ>10%, то примем iв=13%, а iн=12%.
Из таблицы коэффициентов приведения a3;i2=2,38134, a3;iэ=2,36115
Интерполяционное значение ставки:
iэ=12+(2,38134-2,36251)/(2,38134-2,36115)*(13-12)=12,933%
5. 3 Нерегулярный поток платежей.
Задолженность может быть погашена путем выплаты нерегулярного потока платежей:R1,… Rn.
Эффективность кредита при таком способе погашения определим на основе следующего уравнения, балансирующего вложение и отдачи:
f(iэ)=D(1-g)-SRjvtj=0, где tj- интервал от начала сделки до момента выплаты j-го погасительного платежа. Из условия сбалансированности сделки находим, применяя договорную ставку i, величину последнего взноса:
Rn=DqT-SRjqTj, где q=1+iэ;
Т=S Тj, Тj- срок выплаты j-го платежа до конца сделки.
6 Доходность облигаций[9] .Облигации являются наиболее распространенным видом ценных бумаг с фиксированным доходом. Эмитентами облигаций могут быть государство, крупные компании и корпорации, банки и другие финансовые учреждения. Основными параметрами облигаций являются:номинальная цена(N), выкупная цена или правило ее определения, если она отличается от номинала, дата погашения, норма доходности( купонная процентная ставка), даты выплат процентов и погашения.
Т. к. номиналы разных облигаций различаются, то возникает необходимость в сопоставимом измерителе рыночных цен. Курс облигации и выполняет эту функцию, т. е. курсом называют цену одной облигации в расчете на 100 денежных единиц номинала: К=(Р/N)*100, где К- курс облигации, Р-рыночная цена,N –номинал облигации.
При анализе доходности облигаций различают следующие ее виды:
1-купонная доходность – определяется при выпуске облигаций(g),
2-текущая доходность – отношение поступлений по купонам к цене приобретения облигации(it),
3-полная доходность – измеряет реальную эффективность инвестиций в облигацию для инвестора в виде годовой ставки сложных процентов(i).
6. 1 Облигации без обязательного погашения с периодической выплатой процентов.Текущая доходность, как сказано выше, находится следующим образом:
it=gN/P=g*100/К.
Полная доходность: т. к. доход по купонам является единственным источником текущих поступлений, то полная доходность у рассматриваемых облигаций равна текущей в случае, когда вылаты по купонам ежегодные, но, если проценты выплачиваются р – раз в году(по норме g/р), то из уравнения эффективной ставки i = (1+j/m)m-1, получим:
i = (1+(g/р)*(100/К))р-1=(1+ it/р) р –1
Пример№11:Вечная рента, приносящая 3% дохода, куплена по курсу 85. Какова финансовая эффективность инвестиций, при условии, что проценты выплачиваются раз в году, поквартально(р=4)?
i=it=0,03*100/85=0,0353, i=(1+0,0353/4)4-1=0,3577.
6. 2 Облигации без выплаты процентов.В данном случае, доход поступает к владельцу облигации в виде разницы между номиналом и ценой приобретения. Курс такой облигации меньше 100, а для определения ставки помещения приравняем современную стоимость номинала цене приобретения: Nnn=P, или nn =К/100, где n – срок до выкупа облигации, после этого получим:i=1/( nÖ(К/100))-1.
Пример№12:МДМ-банк выпустил облигации с нулевым купоном с погашением через 4 года по курсу реализации-67, доходность облигации в данном случае составит: i=1/( 5Ö(67/100))-1=0,08339, т. е. облигация обеспечивает инвестору 8,34% годового дохода.
6. 3 Облигации с выплатой процентов и номинала в конце срока.В данном случае проценты начисляются за весь срок и выплачиваются одной суммой вместе с номиналом, купонный доход отсутствует, поэтому текущую доходность можно считать нулевой.
Полная доходность находится путем приравнивания современной стоимости дохода цене облигации: (1+g)nNnn=P, или ((1+g)/ (1+i)) n=К/100, Þ i=(((1+g)/(nÖ(К/100))-1.
6. 4 Облигации с периодической выплатой процентов и погашением номинала в конце срока.Владелец данного вида облигаций получает все три показателя доходности.
Текущая доходность рассчитывается по формуле it=gN/P=g*100/К.
Что касается полной доходности, то для ее вычисления необходимо приравнять к цене облигации современную стоимость всех поступлений. Дисконтированная величина номинала-Nnn , тк. поступления по купонам – постоянная рента постнумерандо, то член такой ренты – gN, а современная стоимость составит gNаn,i , или gNа(р)n,i. В итоге получим следующие равенства: Р=Nnn +gNSnt =Nnn +gNаn,i
Разделив на N, находим: К/100=nn +gаn,i, где nn- дисконтный множитель по неизвестной годовой ставке помещения, в зарубежной же практике применяетсяноминальная годовая ставка помещения, причем число раз дисконтирования в году обычно принимается равным числу выплат купонного дохода, тогда (i-номинальная годовая ставка,pn-общее количество купонных выплат,g-годовой процент выплат по купонам):
К/100=(1+i/р)-рn+g/рS(1+i/р)-1=nрn+g/р аn,i/р, далее искомые значения ставки находят приближенными методами (например, интерполяции). Используется так же и метод приближенной оценки:
i@((g+(1-К/100))n)/((1+К/100)/2).
6. 5 Облигации с выкупной ценой, отличающейся от номинала.Это случай, когда проценты начисляются на сумму номинала, а прирост капитала равен С-Р, где С-выкупная цена. Поэтому формулы Р= Nnn +gNаn,i и К/100=nn +gаn,i, приобретут следующий вид: Р= Сnn +gNаn,i и К/100=С/Nnn +gаn,i
А формула метода приближенной оценки приобретет вид:
i@((g+((С/N)-К/100))n)/(((С/N)+К/100)/2).
7 Сравнение коммерческих контрактов. [10]При осуществлении коммерческой деятельности, часто приходится делать выбор между несколькими вариантами сделки, т. к. более низкая цена товара может «компенсироваться» невыгодными для покупателя условиями кредитования ( в данном случае кредитор и продавец рассматриваются как один контрагент, хотя они могут быть и независимыми участниками). Для сравнения условий контрактов используют следующие методы: «классический» подход -задача Клаузберга, и метод, основанный на расчете предельных значений параметров соглашений.
При использовании первого метода, сравниваются современные величины всех платежей, предусмотренных в контракте ( обычно все платежи приводят к моменту времени, в который начинается действие контракта). Современную величину расходов можно трактовать как денежную сумму, которая вместе с начисленными на нее процентами обеспечит все оговоренные в контракте платежи, следовательно, предпочтительнее для должника вариант с меньшей величиной. Дисконтирование проводится по ставке сравнения, которая устанавливается, исходя из экономического прогноза. В зарубежной практике, например, ориентируются на существующий или ожидаемый усредненный уровень ссудного процента. Ставка сравнения отличается от предусмотренных в контракте ставок по кредитам.
Второй метод сравнения легко показать на примере: существует два варианта покупки товара в кредит, первый поставщик продает по цене С1, ставка за кредит i1,Если один из параметров сделки у второго поставщика (С2,i2)не объявлен, то есть возможность определить его максимальное значение, при
котором второй контракт будет конкурентоспособен. Например, С1<С2, тогда определяется максимально допустимое значение i2.
Рассмотрим более подробно «классический» подход сравнения контрактов.
Сравнение условий кредита.
Цена товара постоянна, сравниваются варианты погашения задолженности.
Оговорены следующие условия ее погашения: авансовые платежи (сумма и момент выплаты), продолжительность и условия выплат процентов в льготном периоде, срок и метод погашения. Задача сводится к расчету современных величин для сравниваемых потоков платежей.
Пример№13: Покупателю было предложено оплатить заказ на 7млн. долл. следующим образом: 1)5%- при заключении контракта, 5% - после получения первой партии товаров(6 месяцев), далее в течение 6 лет равные расходы по обслуживанию долга без льготного периода. 2)5%-при заключении контракта, 10% - после получении первой партии, льготный период – 6 месяцев (выплата процентов в конце периода), погашение задолженности в течение 9 лет равными расходами. Введем обозначения:Q1,Q2-суммы авансовых платежей, t-срок выплаты второго авансового платежа, L-срок льготного периода,R-расходы по погашению задолженности, D-остаток задолженности,n=(1+ q )-1,q –ставка сравнения, тогда:
А1= Q1+Q2n t+Rаn,qn t ; А2= Q1+Q2n t+D(1+i)Ln t+L +Rаn,qn t+L
Согласно контракту, погашается сумма, равная цене за вычетом авансовых платежей:D=P-(Q1+Q2). Приравнивая остаток долга современной величине расходов по его обслуживанию, получим R=D/ аn,i. Теперь, можно определить искомые значения А. Процент за кредит положим 10 сложным годовым процентам в обоих случаях, ставка сравнения -15%, остаток задолженности для первого варианта: D=7000-(350+350)=6300, ежегодные расходы: 6300/а6,10=6300/4,3552607=1446,527, коэффициент приведения по ставке сравнения: а6,15=3,784482694, таким образом:
А1=350+350*1,15-0,5+1446,527*3,784482694*1,15-0,5=5781,24,
Для второго варианта:D=7000-(350+700)=5950, проценты за льготный период:5950*(1,10,5-1)=290,413, ежегодные расходы: 5950/а9,10=5950/5,759023816=1033,161, коэффициент приведения по ставке сравнения :а9,15=4,771583920, тогда
А2=350+700*1,15-0,5+290,413*1,15-1+1033,161*4,77158392*1,15-1=5542,08
Таким образом, предпочтительнее оказался второй вариант, т. к. А2<А1.
Сравнение коммерческих контрактов.
Кроме различий в условиях погашения задолженности, включим в задачу различия в цене товара и уровнях процентных ставок. Ниже рассмотрим методы сравнения при условии, что кредиты погашаются после полного выполнения обязательств по поставкам, а на авансовые платежи не начисляются проценты. Добиться однозначного результата можно только, если сроки поставок по вариантам одинаковые.
Пусть аванс выплачивается один раз в начале сделки, предусматривается разовая поставка товара, погашение долга производится равными уплатами, в льготном периоде проценты уплачиваются в конце этого периода. Современная величина по ставке q на момент выплаты аванса для данного случая составит:
А=Q+I+n t+L +Rаn,qn t+L
, где I-проценты в льготном периоде, если R(расходы по обслуживанию долга)- постоянная величина, то R=(P-Q)/аn,i, для варианта без начисления процентов на сумму аванса.
Допустим, проценты определяются по сложной ставке:I=(P-Q)((1+i) L –1), тогда получим:А=Q+(P-Q)[(аn,q/аn,i) n t+L+((1+i) L –1) n t+L],
если проценты периодически выплачиваются в льготном периоде, например, в конце года, то получим, при условии, что L-целое число, следующее:
А=Q+(P-Q)[(аn,q/аn,i) n t+L+iаL,q n t].
Обобщив полученную информацию, можно сказать, что , если А1<А2, i1>i2 и принятой ставке сравнения q0, то найденое соотношение А1 и А2 сохранится для всех других значений q не равно q0, при условии, что q0>i1, или q0<i2.
Если поставки осуществляются последовательно в несколько партий в объемах Мj и сроки Тj, авансовые платежи в сумме Q1 и Q2, льготный период L, оплата задолженности равными расходами в течение n лет. . Тогда накопленная задолженность на конец срока поставки при условии, что на авансовые платежи начисляются проценты, составит:
D=SMj(1+i)Tj-SQk(1+i)Tk
Tj-время от момента поставки до конца срока поставок,Tk-время от момента выплаты авансового платежа до конца поставок,i-договорная процентная ставка.
Размер расходов по обслуживанию долга рассчитывается как R=D/ аn,i, следовательно, современная величина совокупности платежей определяется, при ставке сравнения q, как:
А=Q1+Q2*n t +IаL,q*n T +Rаn,qnT+L
t-срок выплаты второго авансового платежа, аL,q-коэффициент приведения ренты, состоящей из процентных платежей в льготном периоде.
Список литературы«Методы финансовых и коммерческих расчетов», Е. М. Четыркин,М. -95
«Задачи финансового менеджмента»,Л. А. Муравей,М. -98.
[1] «Методы финансовых и коммерческих расчетов»Е.М.Четыркин,М.-1995.
[2] «Методы финансовых и коммерческих расчетов»Е.М.Четыркин,М.-1995.
[3] «Задачи финансового менеджмента»Л.А.Муравей,М.-1998.
[4] «Методы финансовых и коммерческих расчетов»Е.М.Четыркин,М.-1995.
[5] «Методы финансовых и коммерческих расчетов»Е.М.Четыркин,М.-1995.
[6] «Задачи финансового менеджмента»Л.А.Муравей,М.-1998.
[7] «Методы финансовых и коммерческих расчетов»Е.М.Четыркин,М.-1995.
[8] «Методы финансовых и коммерческих расчетов»Е.М.Четыркин,М.-1995.
[9] «Методы финансовых и коммерческих расчетов»Е.М.Четыркин,М.-1995.
[10] «Методы финансовых и коммерческих расчетов»Е.М.Четыркин,М.-1995.
Похожие работы
... на более короткий срок, чем необходимо инвестору. 2 Постановка задачи 2.1 Организационно-экономическая сущность задачи В данном курсовом проекте решается задача автоматизации анализа доходности коммерческого банка от операций с ценными бумагами. В процессе решения поставленной задачи рассчитываются показатели доходности ценных бумаг (ГКО, ОГСЗ и ОФЗ). Существует несколько методов расчета ...
... одного года с момента их приобретения (размещения). Дополнительные акции, которые должны быть оплачены деньгами, оплачиваются при их приобретении в размере не менее 25% от их номинальной стоимости. 2. Анализ доходности ценных бумаг на ЗАО «ВТБ24» Работа на финансовом рынке сопряжена с проблемой учета эффективности данного вида деятельности. Иногда бывает довольно трудно оценить, насколько ...
... банковских процентных ставок с ожидаемыми изменениями в спот-курсе валюты. Из формул (6) и (12) сразу получаем (14) Лекция 4. Обыкновенные акции Основная страница Лекция 1. Базисные финансовые расчеты. Лекция 2. Кредит. Ценные бумаги с фиксированным доходом. Лекция 3. Иностранная валюта. Лекция 4. Обыкновенные акции. Типы акций и параметры акций ...
... (2.2.44) Сложная номинальная процентная ставка (j) (2.2.45) (2.2.46) Сложная учетная ставка (dсл) (2.2.47) (2.2.48) – По мере усложнения задач, стоящих перед финансовым менеджментом, сфера применения непрерывных процентов будет расширяться, так как при этом становится возможным использовать ...
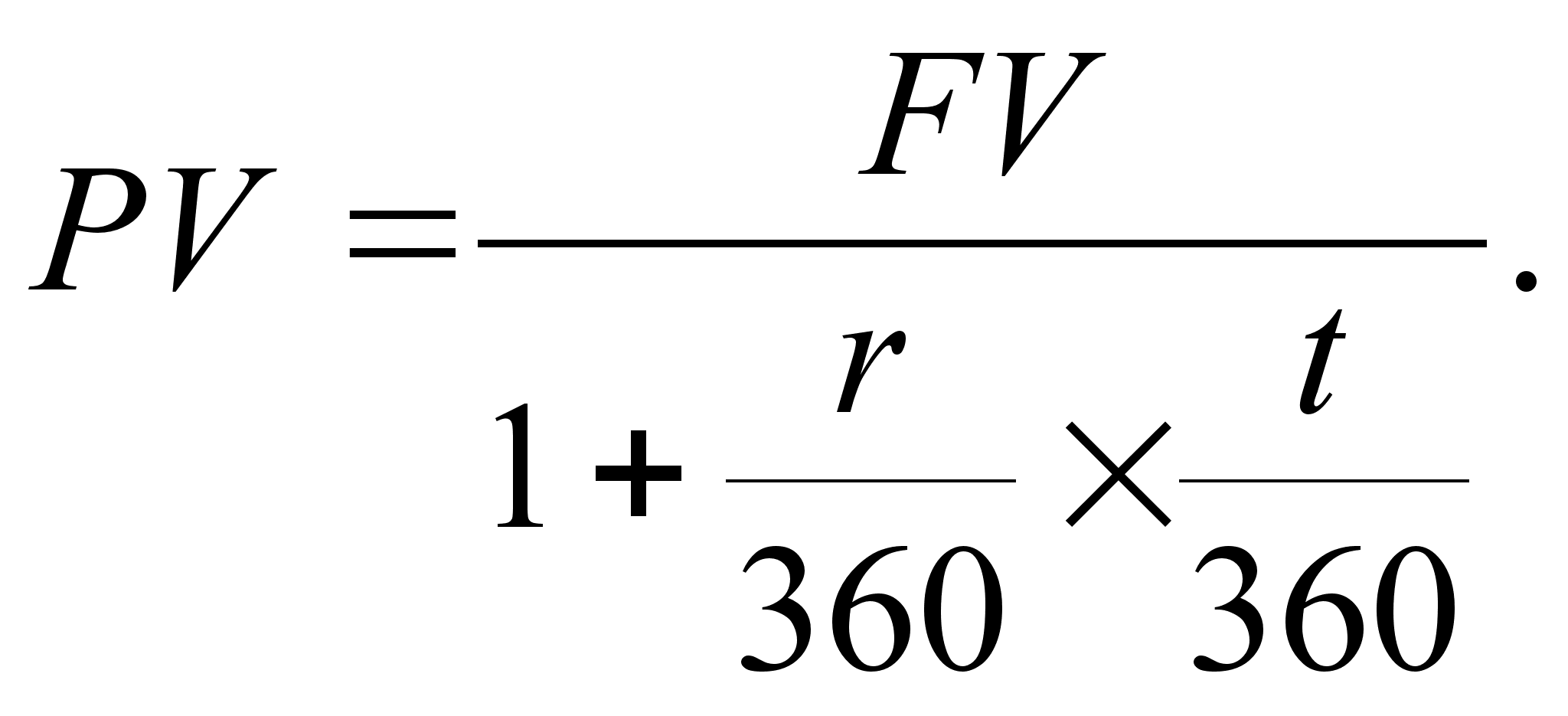


0 комментариев