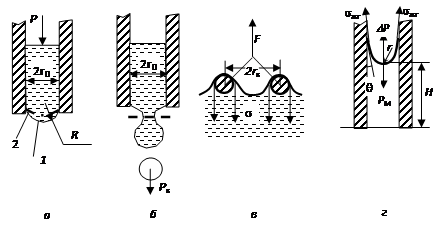
Метод счета капель считается самым простым способом измерения поверхностного натяжения с технической точки зрения. В основе расчетов лежит закон, согласно которому вес капли, отрывающейся от пипетки, пропорционален поверхностному натяжению жидкости ( ) и радиусу пипетки (R) , т.е.
| m=2 R /g , где | (1) |
g - ускорение свободного падения;
m - масса капли исследуемой жидкости.
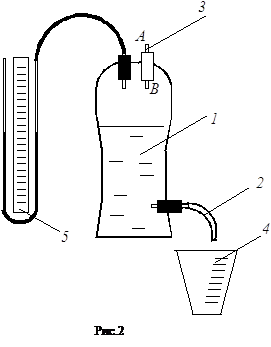
Процесс измерений прост и состоит их двух этапов. На первом этапе определяется радиус пипетки (сталагмометра). Величина радиуса вычисляется по результатам измерения веса капли какой-либо стандартной жидкости, например, дистиллированной воды. Для измерения радиуса не используются какие-либо дополнительные измерительные инструменты, такие как микрометр, поскольку величина радиуса в формуле (1) лишь приближенно отражает действительные размеры используемой пипетки. (Причины такого положения дел будут пояснены далее.)
Второй этап состоит в том, что из пипетки выдавливается несколько капель исследуемой жидкости в посуду для взвешивания. Первая капля не должна попасть в число взвешиваемых. Далее взвешиванием на весах определяется общий вес капель.
Важным является процесс формирования отдельной капли. Формировать каплю быстро недопустимо, так как результат последующего измерения будет недостоверен из-за того, что сила инерции поступающей жидкости оторвет каплю раньше времени. Медленно же формировать каплю не рационально. Обычно поступают следующим образом: каплю формируют быстро, но на последней стадии формирования (до ее отрыва от пипетки) замедляют процесс. Капля должна оторваться при очень медленном поступлении жидкости.
Систематическая ошибка от использования для расчетов формулы (1) достигает в лучшем случае 2-3%, если для калибровки (определения радиуса) применялась дистиллированная вода, а поверхностное натяжение исследуемой пробы равно 20 дин/см. Это связано с тем, что вышеупомянутая формула не совсем верно отражает существующее положение дел. Лонштейн, а затем Гаркинс и Браунс еще в начале века показали, что лучшими показателями обладает формула:
| m=F2 R /g, где | (2) |
F - поправка, зависящая от отношения V/R3;
V - объем капли.
Использование этой формулы для расчетов позволяет определять поверхностное натяжение с точноcтью 0,1-0,2%.
В таблице 1 показаны значения поправок F для различных V/R3. Из таблицы следует, что в действительности образуется капля меньшего размера, чем это предсказывает предыдущая формула (1). Таким образом, расчеты радиуса по раствору с известным поверхностным натяжением дают значение на 40% меньше действительного размера пипетки.
Таблица 1.
| V/R3 | F | V/R3 | F | V/R3 | F |
| 58,1 | 0,215 | 2,3414 | 0,2635 | 0,816 | 0,255 |
| 24,6 | 0,2256 | 2,0929 | 0,26452 | 0,771 | 0,2534 |
| 17,7 | 0,2305 | 1,8839 | 0,26522 | 0,729 | 0,2517 |
| 13,28 | 0,23522 | 1,7062 | 0,26562 | 0,692 | 0,2499 |
| 10,29 | 0,23976 | 1,5545 | 0,26566 | 0,658 | 0,2482 |
| 8,19 | 0,24398 | 1,4235 | 0,26544 | 0,626 | 0,2664 |
| 6,662 | 0,24786 | 1,3096 | 0,26495 | 0,597 | 0,2445 |
| 5,522 | 0,25135 | 1,2109 | 0,26407 | 0,57 | 0,243 |
| 4,653 | 0,25419 | 1,124 | 0,2632 | 0,541 | 0,243 |
| 3,975 | 0,25661 | 1,048 | 0,261 | 0,512 | 0,2441 |
| 3,433 | 0,25874 | 0,98 | 0,2602 | 0,483 | 0,246 |
| 2,995 | 0,26065 | 0,912 | 0,2585 | 0,455 | 0,2491 |
| 2,637 | 0,26224 | 0,865 | 0,257 | 0,428 | 0,2526 |
Расчеты по формуле (2) также предполагают 2 этапа исследований. На первом этапе определяется радиус пипетки по стандартному раствору, а на втором - измерение поверхностного натяжения исследуемой пробы. Расчеты по определению радиуса пипетки усложняется поправкой F, которая зависит от V/R3. Трудность состоит в том, что в формуле (2) радиус фигурирует в 2-х местах. Вычислять его аналитическим путем довольно сложно. В связи с этим лучше знать действительные геометрические размеры пипетки, предварительно измеренные микрометром. Измеренный радиус следует использовать только для вычисления поправки F. Таким образом, радиус по формуле (2) вычисляется довольно просто:
| R = mg/2 стF, где | (3) |
ст - поверхностное натяжение стандартного раствора.
При вычислениях поверхностного натяжения исследуемого раствора применяется тот же принцип: радиус, измеренный микрометром, применяется только для вычисления поправки.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.novedu.ru/
Похожие работы
ная взаимным притяжением молекул жидкости, направленная по касательной к ее поверхности. Действие сил поверхностного натяжения приводит к тому, что жидкость в равновесии имеет минимально возможную площадь поверхности. При контакте жидкости с другими телами жидкость имеет поверхность, соответствующую минимуму ее поверхностной энергии. Понятие «поверхностное натяжение» впервые ввел Я. Сегнер (1752 ...
... при этом работу против межмолекулярных сил. Эта работа в изотермических условиях равна увеличению свободной поверхностной энергии. Для описания термодинамики поверхностных явлений используют два метода: 1. Метод избыточных величин Гиббса. 2. Метод слоя конечной толщины. За толщину поверхностного слоя принимаем расстояние по обе стороны границы раздела ...
... радиус r , длительность течения Dt, коэффициент вязкости h, длина трубы l. На основании этого соотношения разработан и широко применяется метод измерения вязкости жидкостей и газов - метод Пуазейля. [3] Для газов метод предполагает измерение расхода газа при его ламинарном протекании по гладкому, тонкому, капиллярному каналу с известными размерами и при контролируемой разности давлений. В ...
... раз в смену 9. Замер загазованности Площадка нефтесепараторов С1-С6 Содержание углеводородов в воздухе УГ-2 1 раз в смену В связи с непрерывностью технологического процесса на установке первичной подготовки нефти предусмотрена система контроля и сигнализации. Система сигнализации и контроля обеспечивает безопасность работы установки, следя за технологическими параметрами процесса и ...


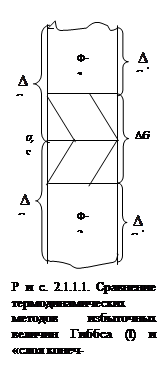
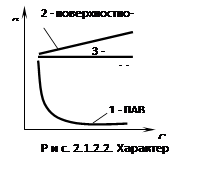



0 комментариев