Реализация дидактических принципов в обучении математике
Обучение математике, как и любому учебному предмету, может стать эффективным средством формирования личности, достичь непосредственной цели - прочного и сознательного усвоения ее содержания - лишь в случае, если в основу обучения будут положены определенные положения, вытекающие из основных закономерностей дидактики, подтвержденные опытом преподавания. Система таких положений, специально ориентированная на особенности математики как учебного предмета, и составляет основное содержание этой главы. В ней описываются наиболее важные принципы, характеризующие подход к обучению математике в школе, - принцип воспитания, принцип научности, принцип сознательности обучения, принцип систематичности и др. Владение этими принципами необходимо будущему учителю для того, чтобы правильно организовать свой труд, грамотно, квалифицированно анализировать различные учебные пособия, которыми ему придется пользоваться в своей работе.
Принципы обучения как категории дидактики
Процесс обучения, являясь составной частью целостного педагогического процесса, в советской школе направлен на формирование всесторонне и гармонически развитой личности.
Обобщенный опыт обучения школьников основам науки показывает, что для обеспечения единого подхода к учащимся, к выбору средств и методов учебной работы учитель должен придерживаться положений, носящих в определенном смысле универсальный характер.
В связи с этим в советской дидактике разработаны принципы, которые рассматриваются как важнейшие требования к организации процесса обучения, его содержанию, формам и методам. Эти единые требования .получили название дидактических принципов или принципов обучения. Организация процесса обучения в соответствии с дидактическими принципами позволяет построить его на научной основе.
Вместе с тем следует иметь в виду, что дидактические принципы, выражая определенные закономерности обучения и передовой опыт учебновоспитательной деятельности школы, не являются раз и навсегда установленными. Они постоянно углубляются и видоизменяются в соответствии с теми задачами, которые ставит перед школой общество.
Таким образом, дидактические принципы - это основные направляющие положения, возникающие в результате анализа научнопедагогических закономерностей и практического педагогического опыта. Они являются главным ориентиром в педагогической работе учителя.
Известные советские дидакты М. А. Данилов, И. Я. Лернер, М. Н. Скаткин в своих исследованиях показали, что принципы обучения, являясь категориями дидактики, характеризуют способы использования законов и закономерностей обучения в соответствии с целями воспитания и образования.
Дидактические принципы - это принципы деятельности, представляющие собой наиболее общее нормативное знание о том, как надо строить, осуществлять и совершенствовать обучение и воспитание. Закономерности этой деятельности являются теоретической основой для выработки норм учебно-воспитательной работы учителя. Однако сами по себе они не содержат конкретных указаний для такой деятельности. Эти указания дают принципы. Таким образом, принципы обучения взаимообусловлены его закономерностями. Например, принцип проблемности в обучении вытекает из закономерности, установленной С. Л. Рубинштейном, состоящей в том, что мышление возникает из проблемной ситуации и направлено на ее разрешение.
Однако, кроме законов и закономерностей обучения в становлении принципов, учитываются и другие факторы, а именно: 1) цели, которые ставит общество перед обучением и воспитанием; 2) конкретные условия, в которых осуществляется учебный процесс; 3) психологические характеристики процесса учения; 4) существующие способы конструирования учебных и воспитательных ситуаций.
Здесь следует заметить, что если речь идет не о дидактическом, а о методическом принципе, то в этом случае должна учитываться специфика конкретного учебного предмета и его функции в общем образовании.
Например, А. А. Столяр предлагает систему дидактических принципов дополнить двумя принципами, характерными для обучения математике:
1) школьный курс математики должен отражать фундаментальные идеи и логику современной математики (в соответствии с уровнем мыслительной деятельности учащихся);
2) процесс обучения математике должен строиться подобно процессу исследования в математике, он должен имитировать процесс творческого поиска в математике (в определенной мере, в какой это допускает уровень мыслительной деятельности учащихся).
Первый принцип относится к построению содержания обучения математике и в определенной степени конкретизирует дидактический принцип научности. Второй принцип относится к построению процесса обучения и конкретизирует дидактический принцип проблемности обучения.
В методической литературе по математике общепризнанной является следующая система дидактических принципов:
1. Принцип воспитания в обучении математике.
2. Принцип научности в обучении математике.
3. Принцип сознательности, активности и самостоятельности в обучении математике.
4. Принцип систематичности и последовательности в обучении математике.
5. Принцип доступности в обучении математике.
6. Принцип наглядности в обучении математике.
7. Принцип индивидуального подхода к учащимся в обучении математике.
8. Принцип прочности знаний в обучении математике.
Принцип воспитания
Общей целью воспитания в школе является подготовка всесторонне развитых людей, способных построить и защитить общество. Всестороннее развитие личности предполагает умственное и нравственное развитие, политехническое образование и профессиональную подготовку, богатую духовную жизнь, физическое и эстетическое развитие. Реализация общей цели воспитания требует поэтому решения более частных задач, которые рассматриваются в качестве составных частей или сторон воспитания. Составными частями воспитания являются трудовое, нравственное, умственное, эстетическое и физическое воспитание.
Выделение составных частей воспитания опирается на объективные требования общества в развитии определенных свойств (качеств) личности. Так как свойства личности формируются не изолированно друг от друга, то и стороны воспитания, находясь во всеобщей взаимосвязи, способствуют формированию целостной личности. Поэтому такие качества целостной личности, как знание, умение, убеждение, поведение и др., могут быть составной частью каждой из указанных выше сторон воспитания.
Но воспитание в процессе обучения вообще и математике в частности как принцип обучения имеет и свою содержательную направленность. Содержательная направленность всех сторон воспитания в обучении определяется формированием коммунистического мировоззрения и морали. Формирование мировоззрения и морали - центральная задача воспитания. Под мировоззрением понимается система философских, научных, политических, нравственных и эстетических представлений и убеждений человека, которая отражает понимание человеком окружающей его природной и социальной среды, его отношение к ней и определяет общую направленность всей его деятельности.
Мораль - это совокупность норм, принципов и правил, регулирующих поведение людей во всех сферах общественной жизни. Воспитание мировоззрения и морали способствует формированию характера каждого школьника. Чтобы учащийся мог действовать в соответствии с принципами мировоззрения и морали, он должен сформировать у себя такие черты характера, как принципиальность, сила воли, скромность, честность по отношению к самому себе и другим людям.
Мировоззрение, базирующееся на научном знании и практическом жизненном опыте, связывает в единое целое эти свойства личности. Отсюда вытекают возможность и необходимость передачи всем людям знаний о закономерностях развития природы, общества и человеческого мышления, чтобы они могли сознательно осуществлять деятельность, направленную на построение общества.
Итак, принцип воспитания подрастающего поколения имеет своей целью воспитание в процессе обучения всесторонне развитой личности на основе формирования мировоззрения и морали.
Следовательно, в формировании убеждений возрастает роль процесса усвоения знаний. В связи с этим в преподавании математики (как и каждого учебного предмета) необходимо повышать активность учащихся и возбуждать у них интерес к вопросам, имеющим мировоззренческое значение. Важную роль в этом приобретает освещение в преподавании математики (также других предметов) новых идей современной науки.
Чтобы в обучении (в частности, математике) реализовывался принцип воспитания, учителю необходимо руководствоваться принципами научности, сознательности, активности и самостоятельности, стимулирования и мотивации положительного отношения школьников к учению и т. п.
Принцип направленности обучения на взаимосвязанное решение задач образования, воспитания и развития учащихся
При планировании содержания, средств, методов и форм обучения учитель призван обеспечить решение всего комплекса образовательных, воспитательных и развивающих задач
Принцип научности
Требование научности содержания образования было выдвинуто в советской педагогической литературе еще в работах Н. К. Крупской (см.: "О работе над новым учебником для новой программы").
Статус дидактического принципа требование научности в обучении приобрело с 1950 г., когда оно было сформулировано и обосновано М. Н. Скаткиным. Было показано, что воспитание человека коммунистического общества непосредственно связано с требованием научности содержания школьного образования.
В дальнейшем Л. Я- Зорина показала, что под научностью содержания образования следует понимать такую его качественную характеристику, которая удовлетворяет трем признакам:
а) соответствие содержания образования уровню современной науки;
б) создание у учащихся верных представлений об общих методах научного познания;
в) показ важнейших закономерностей процесса познания. Эти условия взаимосвязаны между собой, ибо реализация каждого из последующих обусловлена выполнением предыдущих. Каждое предыдущее условие является необходимой базой для реализации последующего.
Первое условие говорит о том, что в соответствии с принципом научности образовательный материал, составляющий содержание школьного обучения, должен в определенной мере соответствовать уровню современной науки. Это требование принципа научности было с достаточной полнотой реализовано в процессе проведенной в последние годы модернизации обучения математике в школе.
Второе условие говорит о том, что принцип научности требует также знания общих методов научного познания. Но это лишь необходимое условие научности знаний. Оно недостаточно для создания у учащихся представлений о процессе познания. Одним из наиболее эффективных методов научного познания действительности в математике является построение математических моделей изучаемых явлений. Метод моделирования широко применяется сейчас в самых разнообразных областях знаний. Поэтому второе требование принципа научности естественным образом выдвигает на первый план обучение школьников доступным для них способам математического моделирования.
Третье условие указывает на то, что принцип научности требует формирования у учащихся представлении о процессе познания и его закономерностях.
В обучении математике у учителя имеется много возможностей показать учащимся закономерности процесса познания. Эти вопросы будут предметом специального рассмотрения в последующих главах. Именно поэтому в процессе обучения основам наук в школе шире должны внедряться проблемное обучение и разнообразные исследовательские приемы. В процессе реализации принципа научности учитель должен соблюдать также принцип доступности, чтобы содержание, формы и методы обучения учитывали реальные возможности учащихся. При этом необходимо учитывать и то, что принцип доступности предполагает обучение на достаточно высоком уровне трудности. Однако это можно достигнуть лишь при наилучшем сочетании индивидуальных и коллективных форм познавательной деятельности школьников в обучении.
Можно выделить три аспекта реализации принципа научности в обучении: 1) реализация его в учебнике (соответствие содержания учебника современному уровню науки); 2) обеспечение высокого научного уровня изложения учебного материала учителем на уроке; 3) выработка у учащихся учебно-исследовательских навыков и умений.
Принцип усиления прикладной направленности обучения
Изучение основ науки должно осуществляться в тесной связи с раскрытием важнейших их применений в промышленности, сельском хозяйстве и общественной жизни. При этом основы науки не должны подменяться ее приложениями.
Использование в обучении математических моделей реальных ситуаций, отбор содержания обучения, отвечающего поставленной цели, представляют собой основные средства реализации принципа связи обучения с жизнью. Важной составной частью этих средств являются задачи и примеры прикладного характера.
Принцип систематичности и последовательности
Нельзя овладеть наукой, не изучая ее в определенной системе. В такой же мере нельзя успешно развивать познавательные и творческие способности учащихся без строго продуманной системы их обучения и воспитания.
" Принцип систематичности и последовательности в обучении обусловливается и логикой самих наук, изучаемых в школе, и особенностями познавательной и практической деятельности учащихся. протекающей в соответствии с закономерностями их умственного и физического развития. Принцип систематичности и последовательности в обучении лежит в основе построения учебных программ, определяет систему работы учителя и деятельность учащихся в процессе обучения"
Принцип систематичности и последовательности в обучении проводится во всей системе учебной работы. Излагать знания систематически - это значит при изучении нового опираться на ранее пройденное, выделять в нем главное, вскрывать общую идею, формировать у учащихся умение анализировать, систематизировать и обобщать изучаемые явления и факты.
Важное значение принцип систематичности и последовательности приобретает в выработке у учащихся умений и навыков самостоятельной работы с книгой, в воспитании у них навыков организованности и последовательности в приобретении знаний.
Систематичность в обучении математике предполагает соблюдение определенной последовательности в изучении учебного материала н постепенное овладение основными понятиями школьного курса математики.
Принцип систематичности ориентирует учителя на достижение системности знаний в сознании учащихся путем установления теснейшей связи между элементами изучаемого материала, раскрытия единства элемента и структуры, части и целого. Следовательно, смысл принципа систематичности заключается в том, что учащиеся осознают приобретенные знания как элементы целостной, единой системы.
Сказанное позволяет утверждать, что научность обучения немыслима без систематичности, а с систематичностью тесно связан вопрос о преемственности в обучении. Ее характеризует опора на пройденное, дальнейшее развитие имеющихся у учащихся знаний, умений н навыков, установление связей между немыми и ранее приобретенными знаниями. В результате этого знания становятся прочными и глубокими.
Систематичность имеет место и в организационных приемах работы учителя - в системе его требований к учащимся. Систематичность должна быть также в учебной деятельности учащихся, в системе методов работы над каждым учебным предметом, в последовательности выполнения домашних заданий и т. п.
Последовательность в обучении математике означает, что обучение осуществляется в соответствии с правилами обучения: а) от простого к сложному; б) от легкого к трудному; в) от известного к неизвестному; г) от представлений к понятиям; д) от знания к умению, а от него к навыку.
Учитель реализует этот принцип, если обучение математике представляет собой цепочку последовательных шагов, каждый из которых последовательно дополняет известные учащимся знания, умения и навыки разумной дозой новых знаний, умений и навыков.
В заключение отметим, что успешная реализация принципа систематичности и последовательности в обучении во многом зависит от того, какое значение придается учителем межпредметным связям в обучении, как скоординированы требования к учащимся между преподавателями различных учебных предметов, соблюдается ли преемственность в изучении отдельных тем и учебных предметов. При этом важное значение приобретает преемственность обучения в младших, средних и старших классах.
Систематические знания характеризуются как знания о научных основах учебного предмета. Они формируются на основе усвоения понятий и фактов в определенной логической последовательности. Наиболее полное свое выражение этот принцип находит в систематических курсах математики. Можно выделить три вида систематизации учебного материала: целевая, логическая и психологическая. В качестве методов систематизации широко применяются индуктивные и дедуктивные методы, аналогия, обобщение, конкретизация и др. Встречаются попытки "ревизии" принципа систематичности, которые выражаются в отказе от изложения в среднем звене обучения основ науки. (Такая идея высказана, например, М. М. Постниковым.) В отдельных странах (например, в Англии, Швеции, Финляндии), по существу, отказались от систематического курса геометрии. Это обстоятельство не замедлило отрицательно сказаться на уровне логического развития учащихся, на их возможностях в усвоении курса математики.
Различают еще системные знания. Они характеризуются, прежде всего, как методологические знания основ научной теории. Одним из средств формирования системных знаний является включение в учебник сведений о математической теории и способах ее построения.
Принцип доступности
Принцип доступности в обучении вытекает из требований учета возрастных особенностей учащихся. Он лежит в основе составления учебных планов и программ.
Принцип доступности требует, чтобы объем и содержание учебного материала были по силам учащимся, соответствовали уровню их умственного развития и имеющемуся запасу знаний, умений и навыков.
Доступность не следует понимать как учение без трудностей. Она не исключает приучение учащихся к преодолению трудностей в учебной деятельности. Это понятно, так как учебная работа требует определенных усилий учащихся в достижении поставленных целей. Суть вопроса заключается не в том, чтобы обходить трудности, а в том, чтобы эти трудности не подрывали, а развивали силы ученика и способствовали повышению результатов учебных занятий.
Реализация принципа доступности предполагает выполнение следующих условий - дидактических правил: а) следовать в обучении от простого к сложному; б) от легкого к трудному; в) от известного к неизвестному.
Отсюда следует, что строгое соблюдение в обучении принципа систематичности и последовательности предопределяет успешную реализацию принципа доступности.
Следовать в обучении от простого к сложному означает, что изучение учащимися фактов, явлений, закономерностей, понятий и т. п. должно начинаться с наиболее простых, с тем чтобы подготовить их к пониманию более сложных. Это положение касается как теоретического, так и практического учебного материала.
Принцип доступности в обучении привлекает к себе особое внимание также в связи с проблемой индивидуального подхода к учащимся и условиях массового обучения.
Принцип доступности требует, чтобы обучение строилось на основе учета возрастных возможностей учащихся. С его помощью регулируется уровень сложности учебного материала, определяется выбор методических подходов изложения его на уроке, правильная дозировка домашних заданий. Слишком упрощенное содержание обучения снижает его развивающие и воспитательные возможности. Поэтому рекомендуется (по Л. В. Занкову), чтобы содержание заданий для учащихся находилось в "зоне их ближайшего развития".
Принцип сознательности, активности, самостоятельности и прочности усвоения
Данный принцип заключается в целенаправленном активном восприятии изучаемых явлений, их осмыслении, творческой переработке и применении. Он вытекает из целей и задач средней школы, призванной готовить активных и самостоятельных членов общества, а также из особенностей процесса обучения, требующего осмысленного и творческого подхода к изучаемому материалу.
Реализация принципа сознательности, активности и самостоятельности в обучении предполагает выполнение следующих условий:
а) соответствие познавательной деятельности учащихся закономерностям процесса учения;
б) познавательная активность учащихся в процессе учения;
в) осознание школьниками процесса учения;
г) владение учащимися методами умственной работы в процессе познания "нового".
Остановимся кратко на сущности этой совокупности условий. Учебное познание есть учение, т. е. деятельность учащихся по усвоению новых знаний и способов деятельности. Следовательно, говоря об усвоении, мы имеем в виду познавательную деятельность учащихся (процесс учения), но всегда в единстве с руководящей, обучающей ролью учителя и содержанием учебного материала с учетом его структуры.
Отсюда следует, что сущность процесса обучения в целом и его составной части - учения (усвоения) заключается в том, что этот процесс вытекает из общего хода процесса познания и его закономерностей. В соответствии с ним дидактика выделяет в процессе усвоения диалектически взаимосвязанные этапы познавательной деятельности учащихся: восприятие - осмысление - закрепление - применение.
Если в процессе познания нового учащиеся будут совершать умственные и практические действия в соответствии с выделенными этапами процесса учения, включающими в себя действия по восприятию изучаемого материала, его осмыслению (пониманию), закреплению и применению, то можно утверждать, что в обучении созданы условия для активизации познавательной деятельности учащихся и осознания ими процесса учения.
Здесь следует обратить внимание на три обстоятельства. Во-первых, процесс познавательной деятельности в каждом отдельном случае не обязательно проходит по всем этапам учебного познания и в указанной последовательности. Например, при дедуктивном рассуждении учащимся нет необходимости проходить этап восприятия изучаемых явлений и формирования соответствующих представлений. Так, при усвоении нового знания о том, что всякое сечение шара плоскостью есть круг, учащимся предлагается конкретный факт - данная плоскость пересекает шар - и общее правило относительно всех плоскостей, пересекающих шар, - всякое сечение шара плоскостью есть круг.. Применив это общее правило к конкретному факту, учащиеся приходят к одному и тому же выводу: "Следовательно, данное сечение есть круг". Во-вторых, выделенные выше четыре условия реализации принципа сознательности, активности и самостоятельности не являются независимыми. Выполнение первого условия означает выполнение остальных. Однако выделение такой совокупности условий раскрывает дидактический механизм действия самого принципа, что важно и необходимо знать учителю. В-третьих, чтобы в обучении было установлено соответствие познавательной деятельности учащихся закономерностям процесса учения (первое условие), необходима целенаправленная деятельность учителя по формированию у учащихся ответственного отношения к приобретению и усвоению знаний, их осмысливанию и практическому применению. Только в результате такой управляющей деятельности учителя можно говорить о реализации принципа сознательности, активности и самостоятельности учащихся в обучении.
Сознательность понимается в дидактике как овладение учащимися данными науки, учебным материалом, глубокое осмысление его, умение пользоваться знаниями на практике в новых условиях, превращение знаний в убеждения, в руководство к действию.
В процессе сознательного усвоения знаний формируется творческое отношение к изучению и применению знаний, логическое мышление учащихся и их мировоззрение. Сознательное усвоение знаний исключает догматическое, при котором учащиеся принимают на веру преподносимые учителем знания. Результатом догматического усвоения является формализм знаний. Основными признаками формализма знаний являются отсутствие конкретных представлений об изучаемых явлениях; запоминание без понимания, без умения творчески применять знания на практике; безынициативность; отсутствие высоких общественных идеалов, глубоких убеждений и готовности бороться за них.
Конкретно в обучении математике формализм в знаниях особенно часто проявляется в том, что учащиеся безошибочно дают формулировку определения того или иного понятия, но не могут им воспользоваться при решении задач, доказательстве теорем.
В теории обучения выявлены признаки осознанности знаний, которыми может руководствоваться учитель в процессе обучения. К ним относится следующая совокупность признаков:
а) понимание учащимися характера связей между знаниями (рядоположности и соподчиненности, степени их существенности);
б) понимание механизма становления и проявления связей;
в) умение обосновывать знания;
г) понимание способов получения знаний и сферы их применения. Сознательное обучение обязательно предполагает активную деятельность учащихся в этом процессе.
Активность есть деятельное состояние учащегося, которое характеризуется стремлением к учению, умственным напряжением и проявлением волевых усилий в процессе овладения знаниями. Такую активность учащихся в обучении называют познавательной активностью.
В учебном процессе активность учащихся получает свое выражение не только в работе мысли, но и в практической деятельности, в общественной работе, в волевом напряжении и в эмоциональных переживаниях.
Умственная активность учащихся в процессе обучения математике имеет особо важное значение при формировании понятий. Поэтому учителю необходимо владеть методическими приемами, возбуждающими мыслительную активность учащихся в этом процессе.
Активность учащихся в обучении проявляется в их инициативности и высокой степени самостоятельности (или познавательной самостоятельности).
Познавательная самостоятельность является высшей формой активности и сознательности учащихся в процессе учения. Поэтому осуществление в обучении сознательного и активного процесса учения неизбежно формирует такое важное качество личности, как познавательная самостоятельность, которая является важнейшей характеристикой деятельности школьника в учебном процессе.
В теории обучения выделены признаки познавательной самостоятельности учащихся. К ним относятся стремление и умение самостоятельно мыслить; способность ориентироваться в новой ситуации, найти свой подход к решению новой задачи; желание понять не только усваиваемые знания, но и способы их добывания; критический подход к суждению других; независимость собственных суждений. Большое значение в плане формирования познавательной активности и самостоятельности учащихся имеют самостоятельные работы. Самостоятельные работы являются формой совместной единой деятельности учителя и учащихся. Выполняя самостоятельную работу, учащиеся активно оперируют приобретенными знаниями, умениями и навыками, совершают поисковую деятельность. Поэтому в этой самостоятельной деятельности учащегося укрепляются и взаимообусловливаются его познавательная активность и самостоятельность, а такая деятельность отличается высоким уровнем сознательности.
Если в результате обучения учащиеся приобрели такое качество личности, как познавательная самостоятельность, то можно утверждать, что на всех этапах учебного познания реализовывался дидактический принцип сознательности, активности и самостоятельности в обучении.
Сознательное усвоение характеризуется: пониманием изученного, осознанием путей получения нового знания, умением применять знания.
Применение знаний связано с "переносом" их в те или иные ситуации. Возможность осуществления учащимися переноса более высокого уровня (на более отдаленную, необычную, существенно отличающуюся от первоначальной новую ситуацию) свидетельствует о высокой степени сознательности усвоения.
Сознательное усвоение помогает избежать формализма в знаниях. Различаются два вида формализма (по Я. С. Дубнову):
1) ученик не видит связи математических понятий и фактов с реальным миром - формализм первого вида;
2) ученик воспроизводит определение, но не понимает его смысла (например, формулирует определение логарифма, но не может найти log100) - формализм второго вида.
Прочность усвоения может быть обеспечена четким выделением главного в учебном материале, выявлением внутренних и внешних связей изучаемого материала (например, с помощью логико-структурных схем), продуманной системой повторения и применения знаний, дифференцированным подходом к объяснению наиболее сложных мест учебного материала.
Принцип наглядности
Теоретическое обоснование принципу наглядности впервые было дано чешским педагогом Я.А. Коменским, который выдвинул требование учить людей познавать самые вещи, а не только чужие свидетельства о них.
Русский педагог К.Д. Ушинский указывал, что наглядность отвечает психологическим особенностям детей, мыслящих "формами, звуками, красками, ощущениями". Наглядное обучение, по словам К. Д. Ушинского, "строится не на отвлеченных представлениях и словах, а на конкретных образах, непосредственно воспринятых ребенком". Наглядность обогащает круг представлений ребенка, делает обучение более доступным, конкретным и интересным, развивает наблюдательность и мышление.
Принцип наглядности вытекает из сущности процесса восприятия, осмысления и обобщения учащимися изучаемого материала. Он означает, что в обучении необходимо, следуя логике процесса усвоения знаний, на каждом этапе обучения найти его исходное начало в фактах и наблюдениях единичного или в аксиомах, научных понятиях. и теориях, после чего определить закономерный переход от восприятия единичного, конкретного предмета к общему, абстрактному или, наоборот, от общего, абстрактного к единичному, конкретному. Таким образом, советская дидактика исходит из единства чувственного и логического, считает, что наглядность обеспечивает связь между конкретным и абстрактным, содействует развитию абстрактного мышления, во многих случаях служит его опорой. Однако характер и степень использования наглядности различны на разных этапах обучения. Излишнее увлечение наглядностью в обучении может привести к нежелательным результатам. Конкретная наглядность (например, рассмотрение моделей геометрических тел) должна постепенно уступать место абстрактной наглядности (рассмотрению плоских чертежей).
Говоря о значении принципа наглядности и о его роли в процессе учебного познания, дидактика утверждает, что наглядность является исходным моментом обучения главным образом в младших классах. По мере движения учащихся к старшим классам учитель постепенно должен находить в обучении историко-индуктивный путь пополнения знаний: постановка проблемы, история ее решения и современное состояние, затем практические или лабораторные работы. Здесь наглядность получает свою реализацию дважды: как иллюстрация истории открытия и как способ раскрытия современного решения проблемы.
Однако исторический подход занимает много времени и не всегда необходим. Поэтому исходным началом могут быть теоретические положения, аксиомы, системы понятий, усвоенные учащимися на предшествующих этапах обучения. В этом случае наглядность используется лишь для иллюстрации усвоенных учащимися знаний в процессе их применения к решению задач. По характеру отражения окружающей действительности различают следующие виды наглядности:
натуральная (естественная) наглядность, представляющая собой реальные предметы или процессы (объекты и явления, раздаточный материал и др.);
изобразительная наглядность (фотографии, художественные картины, рисунки, учебные картины и др.) применяется, когда показ натурального предмета затруднен, а созерцание конкретного образа необходимо;
символическая наглядность (чертежи, графики, схемы, таблицы, диаграммы) по существу является своеобразным языком, а потому должна специально изучаться, чтобы стать понятной. Например, при изучении свойств функций (возрастание, убывание, максимум, минимум и др.) целесообразно их аналитическую запись переводить на язык графиков и на этой основе тренировать учащихся "читать" графики функций.
Различные виды наглядности выполняют различные функции. Одни содействуют оживлению представлений (картины, предметы жизни), другие являются опорой для отвлеченного мышления.
Наглядность применяется и как средство познания нового, и для иллюстрации мысли, и для развития наблюдательности, и для лучшего запоминания материала. Средства наглядности используются на всех этапах процесса обучения: при объяснении нового материала учителем, при закреплении знаний, формировании умений и навыков, при выполнении домашних заданий, при контроле усвоения учебного материала.
Применение наглядных пособий в обучении подчинено ряду правил: ориентировать учащихся на всестороннее восприятие предмета с помощью разных органов чувств;
обращать внимание учащихся на самые важные, существенные признаки предмета;
показать предмет (по возможности) в его развитии; предоставить учащимся возможность проявлять максимум активности и самостоятельности при рассмотрении наглядных пособий;
использовать средств наглядности ровно столько, сколько это нужно, не допускать перегрузки обучения наглядными пособиями, не превращать наглядность в самоцель.
Следовательно, умелое применение средств наглядности в обучении всецело находится в руках учителя. Учитель в каждом отдельном случае должен самостоятельно решать, когда и в какой мере надо применять наглядность в процессе обучения, ибо от этого в определенной степени зависит качество знаний учащихся.
Принцип наглядности, по выражению Я. А. Коменского, является "золотым правилом дидактики". Он требует сочетания наглядности и мысленных действий, наглядности и слова. Вредным является как недостаточное, так и избыточное применение средств наглядности. Их недостаток приводит к формальным знаниям, а избыток может затормозить развитие логического мышления, пространственного представления и воображения. Встречаются примеры нетрадиционного применения принципа наглядности.
Принцип индивидуального подхода к учащимся
Повышение эффективности обучения непосредственно связано с тем, насколько полно учитываются особенности каждого учащегося. Важной индивидуальной особенностью учащихся является их способность к усвоению знаний, т. е. обучаемость. Под влиянием возрастающих требований жизни увеличивается объем и усложняется содержание знаний, подлежащих усвоению в школе. Чем глубже развивается этот процесс, тем более четко выступают индивидуальные различия в обучаемости школьников.
Как показали многочисленные психолого-дидактические исследования, если уровнять многие факторы, влияющие на уровень усвоения новых знаний, а именно: обеспечить одинаковый исходный минимум знаний у всех учащихся, положительное отношение их к уроку, желание как можно лучше усвоить материал, тщательно разработать методику введения нового материала, то, несмотря на равенство этих условий, новые знания будут усвоены поразному. Одни школьники достаточно полно усвоят новое и могут применить его в новых, но сходных с учебной обстановкой условиях, требующих самостоятельного развития новых знаний (высший уровень усвоения). Другие усвоят существенные стороны нового понятия или закономерности и сумеют применить их к решению задач, близких к тем, которые разбирались в процессе объяснения нового материала (средний уровень усвоения). Наконец, будут и такие, кто вынес лишь отдельные, нередко несущественные стороны нового понятия или закономерности и не может применить их к решению даже простых задач (низший уровень усвоения). При этом потребуется различное количество упражнений и различная мера помощи со стороны учителя тем учащимся, которых предстоит довести до высшего уровня усвоения.
В психологии обучения выявлено несколько характеристик индивидуальных различий учащихся, связанных с понятием обучаемости. К ним относятся: а) темп усвоения или продвижения в обучении как наиболее устойчивая характеристика; б) полнота и точность анализа и синтеза и неразрывно связанных с ними обобщения и абстрагирования; в) устойчивая предрасположенность школьников к тому или иному виду анализа, особенно при первичной работе над материалом; г) уровень формируемых у школьника обобщений; д) уровень выделения и обобщения школьниками способов оперирования знаниями; е) экономичность мышления и др.
Следует заметить, что предпоследняя (указанная здесь) сторона мыслительной деятельности позволила психологам сделать предположение о том, что не всякое усвоение знаний означает сдвиг в умственном развитии учащегося. Этот сдвиг происходит тогда, когда обучение обеспечивает овладение не только содержанием знаний, но и методами, способами их приобретения, благодаря чему учащиеся могут самостоятельно приобретать новые знания.
Отмеченные выше явления, имеющие место в обучении школьников, показали невозможность создать в обучении систему, равно оптимальную для каждого учащегося. Это обстоятельство привело к необходимости реализации в обучении принципа индивидуального подхода к учащимся. Сущность принципа индивидуального подхода по существу состоит в адаптации (приспособлении) обучения либо к содержанию и уровню знаний, умений и навыков каждого учащегося, либо также к характерным для него особенностям процесса усвоения, либо даже к некоторым устойчивым особенностям его личности. Основным средством реализации принципа индивидуального подхода являются индивидуальные самостоятельные работы, предназначенные для учащихся. Они выступают в качестве специфического дидактического средства организации и управления самостоятельной деятельностью учащихся на всех этапах обучения.
Принцип прочности знаний
Принцип прочности знаний обусловливается как задачами школы, так и закономерностями процесса обучения. Опираться на приобретенные знания, умения и навыки можно лишь в том случае, когда они усвоены твердо и длительное время удерживаются в памяти.
Прочные знания, умения и навыки необходимы как для успешного продолжения образования, так и для формирования у учащихся научного мировоззрения, развития их способностей, подготовки к практической деятельности.
В дидактике сформулированы условия прочности знаний. К ним относятся:
активное приобретение знаний с целью сознательного их усвоения; научность обучения;
создание в обучении условий для запоминания учебного материала.
Содержание и сущность принципов научности и сознательности в обучении было раскрыто выше. Поэтому рассмотрим некоторые основы механизма запоминания в процессе обучения.
Запоминание есть процесс памяти, в результате которого происходит закрепление нового путем связывания его с ранее приобретенным. Запоминание всегда избирательно: в памяти сохраняется не все, что оказывает воздействие на органы чувств индивида. От чего это зависит? Запоминание является закономерным продуктом действия субъекта с объектом, т. е. запоминается то, с чем человек действует. При этом успешность запоминания учебного материала определяется мотивами, целями и способами деятельности личности. Назовем основные условия запоминания материала в обучении: учебный материал запоминается учащимися лучше, если он входит в содержание основной цели деятельности. Например, если целью действий учащихся является выявление свойств той или иной геометрической фигуры, то их запоминание будет лучшим, нежели в том случае, когда свойства фигуры сообщаются непосредственно учителем; учебный материал запоминается лучше, если он вызывает активную умственную работу над ним. Поэтому материал более трудный запоминается лучше, чем легкий, так как связи между элементами трудного текста являются более содержательными.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://pedagogika.by.ru/
Похожие работы
... применения в организации занятий по развитию математических представлений общедидактических принципов. [13] II. Экспериментальная работа по применению общедидактических принципов в организации занятий по развитию математических представлений в ДОО 2.1 Констатирующий этап эксперимента Для проведения экспериментальной работы мною была выбрана средняя группа № 4 МДОУ «Бендерский Детский сад ...
... научного знания, с принципами построения научных теорий в единстве и противоположности математики и естественных и гуманитарных наук, с критериями истинности в разных формах человеческой деятельности. Заключение В исследовании внимание уделяется поиску конкретных новых событий и явлений и последовательному изложению выверенных фактов истории развития методики преподавания математики в России
... при ошибке в его выборе, учитывать по уровневый подход. 4. Математика должна входить в набор обязательных учебных предметов любого из профилей.2 МАТЕМАТИЧЕСКИЙ ФАКУЛЬТАТИВ КАК ВЕДУЩАЯ ФОРМА ПРОФИЛЬНОГО ОБУЧЕНИЯ МАТЕМАТИКЕ В ОБЩЕОБРАЗОВАТЕЛЬНОЙ ШКОЛЕ2.1. Организационно-педагогические условия успешного функционирования математических факультативов Еще на рубеже XIX и XX вв. некоторые ...
... поколения, поставленными обществом. Методика обучения математике призвана исследовать проблемы математического образования, обучения математике и математического воспитания. Методика преподавания математики в средней школе возникла с целью поиска педагогически целесообразных путей и способов изложения учебного материала. Методика преподавания математики начала разрабатываться чешским учёным ...
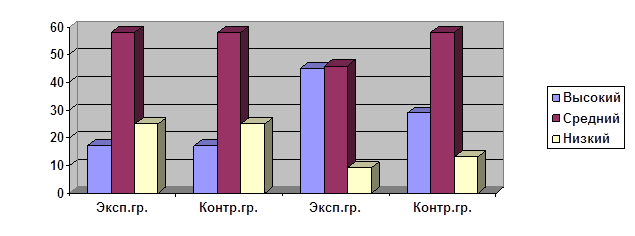

0 комментариев