Суммарная АЭ - число зарегистрированных превышений (выбросов) АЭ-сигналов установленного уровня в течение заданного интервала времени

3. Суммарная АЭ - число зарегистрированных превышений (выбросов) АЭ-сигналов установленного уровня в течение заданного интервала времени.

В случае дискретной АЭ эта величина характеризует число событий с энергией, превышающей установленное пороговое значение. При регистрации дискретной АЭ теряется часть ин­формации, связанная с импульсами, амплитуда которых мень­ше установленного порога - уровня дискриминации. Кроме то­го, возможность произвольного выбора этого уровня делает па­раметр неоднозначным. Если производить счет недетектированных импульсов, представляющих затухающие осциллирую­щие сигналы, поступающие с пьезоприемника, что практику­ется довольно часто, то появляется дополнительная неодно­значность результатов, обусловленная многократной регистра­цией одного и того же первичного импульса. При этом крат­ность воспроизведения его в счетном устройстве зависит от уровня дискриминации, коэффициента затухания колебаний в объекте и преобразователе, а также характеристик приемно-усилительного тракта.

4. Скорость счета  - число зарегистрированных превы­шений АЭ-сигналов установленного уровня в единицу времени.

Эта характеристика является производной суммарной АЭ по времени и обладает теми же недостатками. Некоторые авто­ры называют этот параметр интенсивностью АЭ.

5. Плотность вероятности амплитуды импульсов w(A) характеризует АЭ уже как случайный процесс. Эта функция определяет вероятность того, что амплитуда АЭ-импульса А₀ находится в интервале от А до А + dA :

Р {А < A₀ < А + dA} = w{A)dA.

На практике чаще используют характеристику n(А), назы­ваемую амплитудным распределением импульсов. Эта функ­ция указывает количество импульсов, амплитуда которых за­ключена в малом интервале от А до A+dA . Если общее чи­сло зарегистрированных импульсов равно N , то амплитудное распределение связано с плотностью вероятности w(A) соот­ношением

n(А) = N*w(A),

причем

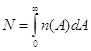Функции w(A) и n(А) можно оценить по эксперименталь­ным данным, построив гистограмму распределения импульсов АЭ по амплитуде. Как известно, эта гистограмма отражает за­висимость количества импульсов n_i (или доли таких импуль­сов n_i/N), амплитуда которых заключена в малом интервале от А_i до A_i +  ,от величины амплитуды А_i. Нетрудно уста­новить взаимосвязь между этими функциями:

Nw(A_i)= n(A_i) = n_i.

Определив по экспериментальным данным с использованием этих соотношений набор значений функций w(A_i) и n(A_i), в дальнейшем, например при помощи системы распределений Пирсона, можно подобрать аналитические вы­ражения для описания функций w(A) или n(А).

6. Распределение временных интервалов  между от­дельными АЭ-импульсами содержит важную информацию о физике явления и характере его развития. При взаимной независимости и одинаковой вероятности элементарных событий их последовательность (поток событий) описывается законом Пуассона. Если поток стационарен, то распределение интерва­лов времени между импульсами АЭ подчиняется экспоненциальному закону

причем среднее значение временного интервала между импуль­сами составляет величину . Справедливо и обратное утверждение - при экспоненциальном распределении интерва­лов между отдельными событиями, последние распределены по закону Пуассона. Такое заключение свидетельствует об отсут­ствии взаимосвязи отдельных событий, что само по себе слу­жит важной информацией о характере процесса. Например, о делокализованном разрушении материала конструкции.

7. Амплитудно-временное распределение импульсов АЭ n(A;t) – функция, указывающая количество импульсов АЭ dN, зарегистрированных в промежутке времени от t до t+dt амплитуда которых заключена в интервале от А до А + dA:

dN = n(A,t)dAdt.

Если эту функцию проинтегрировать по времени от 0 до Т - времени регистрации АЭ, найдем амплитудное распределе­ние импульсов АЭ, а проинтегрировав еще раз по амплитуде, получим общее число импульсов за время регистрации:

Другими словами, амплитудно-временное распределение отра­жает изменение амплитудного распределения импульсов АЭ во времени.

8. Спектральная плотность S(w) дискретной АЭ совпада­ет с соответствующей характеристикой случайного процесса и равна мощности процесса в единичной полосе частот.

Информативность спектральной плотности обусловлена ее связью со скоростью протекания процесса, инициирующего сиг­налы АЭ. Кроме спектральной плотности для анализа акусти­ческой эмиссии в ряде случаев бывает удобнее использовать корреляционную функцию. Информативное содержание этой ха­рактеристики то же, что и у спектральной плотности, посколь­ку между собой они связаны прямым и обратным преобразова­нием Фурье [46].

Для непрерывной АЭ меняется содержание некоторых из указанных характеристик. Кроме того, могут быть введены до­полнительные параметры для описания процесса. Так как те­ряется смысл понятия амплитуды отдельного импульса, сум­марная АЭ и скорость АЭ определяются числом выбросов слу­чайного процесса над уровнем дискриминации, т.е. числом пре­вышений регистрируемой величиной (электрическим напряже­нием, током) установленного уровня дискриминации за все вре­мя регистрации или за единицу времени соответственно. Вме­сто амплитудного распределения следует использовать плот­ность вероятности АЭ, определяющую долю времени наблюде­ния, в течение которого регистрируемая величина находится в интервале вблизи заданного значения амплитуды. Кроме того, вводятся одномерные и многомерные функции распределения указанных выше параметров.