Алгоритм методу

2.1. Алгоритм методу

 1. Визначаємо з даного диференціального рівняння другого порядку функції

.

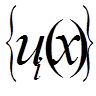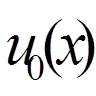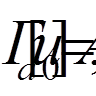
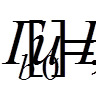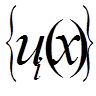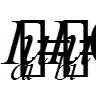2. Обираємо систему базисних функцій  ( = 0, 1, . . . , n) так, щоб функція  задовольняла крайовим умовам:  а функції  ( = 1, 2, . . . , n) задовольняли б однорідним крайовим умовам  ( = 1, 2, . . . , n).

 3. Знаходимо 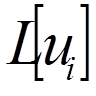( = 0, 1, 2, 3, 4).

 4. Використовуючи позначення

, 

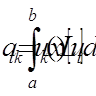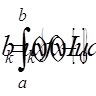
обраховуємо коефіцієнти системи:

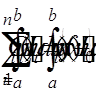 ( = 1, 2, . . . , n).

5. Виконуючи необхідні скорочення приходимо до системи з якої визначаємо 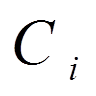 ( = 1, 2, . . . , n) і отримуємо розв’язок вигляді:

.

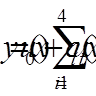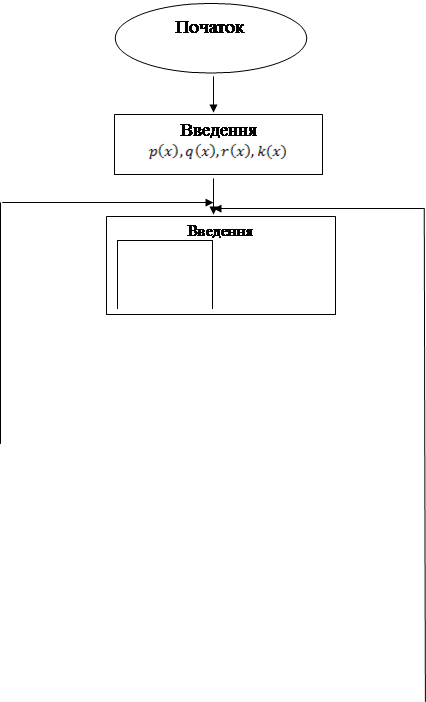
2.2. БЛОК-СХЕМА АЛГОРИТМУ

Метод Галеркіна

 

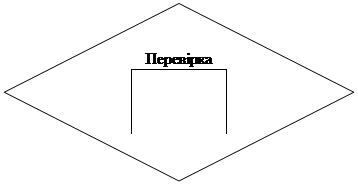Ні

 

Так

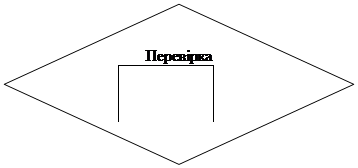Ні

 

Так

	Обрахунок ( = 0, 1, 2, 3, 4)

 

	Обрахунок ,