Навигация
0.0 Конец декодирования
Это основная идея арифметического кодирования, его практическая реализация несколько сложнее. Некоторые проблемы можно заметить непосредственно из приведенного примера.
Первая состоит в том, что декодеру нужно обязательно каким-либо образом дать знать об окончании процедуры декодирования, поскольку остаток 0,0 может означать букву а или последовательность аа, ааа, аааа и т.д. Решить эту проблему можно двумя способами.
Во-первых, кроме кода данных можно сохранять число, представляющее собой размер кодируемого массива. Процесс декодирования в этом случае будет прекращен, как только массив на выходе декодера станет такого размера.
Другой способ – включить в модель источника специальный символ конца блока, например #, и прекращать декодирование, когда этот символ появится на выходе декодера.
Вторая проблема вытекает из самой идеи арифметического кодирования и состоит в том, что окончательный результат кодирования – конечный интервал – станет известен только по окончании процесса кодирования. Следовательно, нельзя начать передачу закодированного сообщения, пока не получена последняя буква исходного сообщения и не определен окончательный интервал? На самом деле в этой задержке нет необходимости. По мере того, как интервал, представляющий результат кодирования, сужается, старшие десятичные знаки его (или старшие биты, если число записывается в двоичной форме) перестают изменяться (посмотрите на приведенный пример кодирования). Следовательно, эти разряды (или биты) уже могут передаваться. Таким образом, передача закодированной последовательности осуществляется, хотя и с некоторой задержкой, но последняя незначительна и не зависит от размера кодируемого сообщения.
И третья проблема – это вопрос точности представления. Из приведенного примера видно, что точность представления интервала (число десятичных разрядов, требуемое для его представления) неограниченно возрастает при увеличении длины кодируемого сообщения. Эта проблема обычно решается использованием арифметики с конечной разрядностью и отслеживанием переполнения разрядности регистров.
Кодирование длин повторенийКодирование длин участков (или повторений) может быть достаточно эффективным при сжатии двоичных данных, например, черно-белых факсимильных изображений, черно-белых изображений, содержащих множество прямых линий и однородных участков, схем и т.п. Кодирование длин повторений является одним из элементов известного алгоритма сжатия изображений JPEG.
Идея сжатия данных на основе кодирования длин повторений состоит в том, что вместо кодирования собственно данных подвергаются кодированию числа, соответствующие длинам участков, на которых данные сохраняют неизменное значение.
Предположим, что нужно закодировать двоичное (двухцветное) изображение размером 8 х 8 элементов, приведенное на рис. 1.
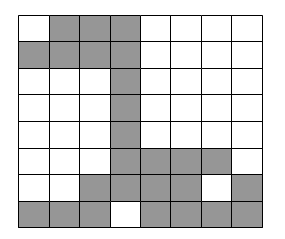
Рис. 1
Просканируем это изображение по строкам (двум цветам на изображении будут соответствовать 0 и 1), в результате получим двоичный вектор данных
X= (0111000011110000000100000001000000010000000111100011110111101111)
длиной 64 бита (скорость исходного кода составляет 1 бит на элемент изображения).
Выделим в векторе X участки, на которых данные сохраняют неизменное значение, и определим их длины. Результирующая последовательность длин участков - положительных целых чисел, соответствующих исходному вектору данных X, - будет иметь вид r = (1, 3, 4, 4, 7, 1, 7, 1, 7, 1, 7, 4, 3, 4, 1, 4, 1, 4).
Теперь эту последовательность, в которой заметна определенная повторяемость (единиц и четверок гораздо больше, чем других символов), можно закодировать каким-либо статистическим кодом, например, кодом Хаффмена без памяти, имеющим таблицу кодирования (табл. 2)
Таблица 2
| Кодер | |
| Длина участка | Кодовое слово |
| 4 | 0 |
| 1 | 10 |
| 7 | 110 |
| 3 | 111 |
Для того, чтобы указать, что кодируемая последовательность начинается с нуля, добавим в начале кодового слова префиксный символ 0. В результате получим кодовое слово B (r) = (0100011010110101101011001110100100) длиной в 34 бита, то есть результирующая скорость кода R составит 34/64, или немногим более 0,5 бита на элемент изображения. При сжатии изображений большего размера и содержащих множество повторяющихся элементов эффективность сжатия может оказаться существенно более высокой.
Ниже приведен другой пример использования кодирования длин повторений, когда в цифровых данных встречаются участки с большим количеством нулевых значений. Всякий раз, когда в потоке данных встречается “ноль”, он кодируется двумя числами. Первое - 0, являющееся флагом начала кодирования длины потока нулей, и второе – количество нулей в очередной группе. Если среднее число нулей в группе больше двух, будет иметь место сжатие. С другой стороны, большое число отдельных нулей может привести даже к увеличению размера кодируемого файла:
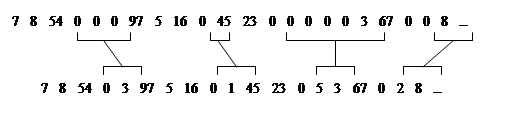
Еще одним простым и широко используемым для сжатия изображений и звуковых сигналов методом неразрушающего кодирования является метод дифференциального кодирования.
Похожие работы
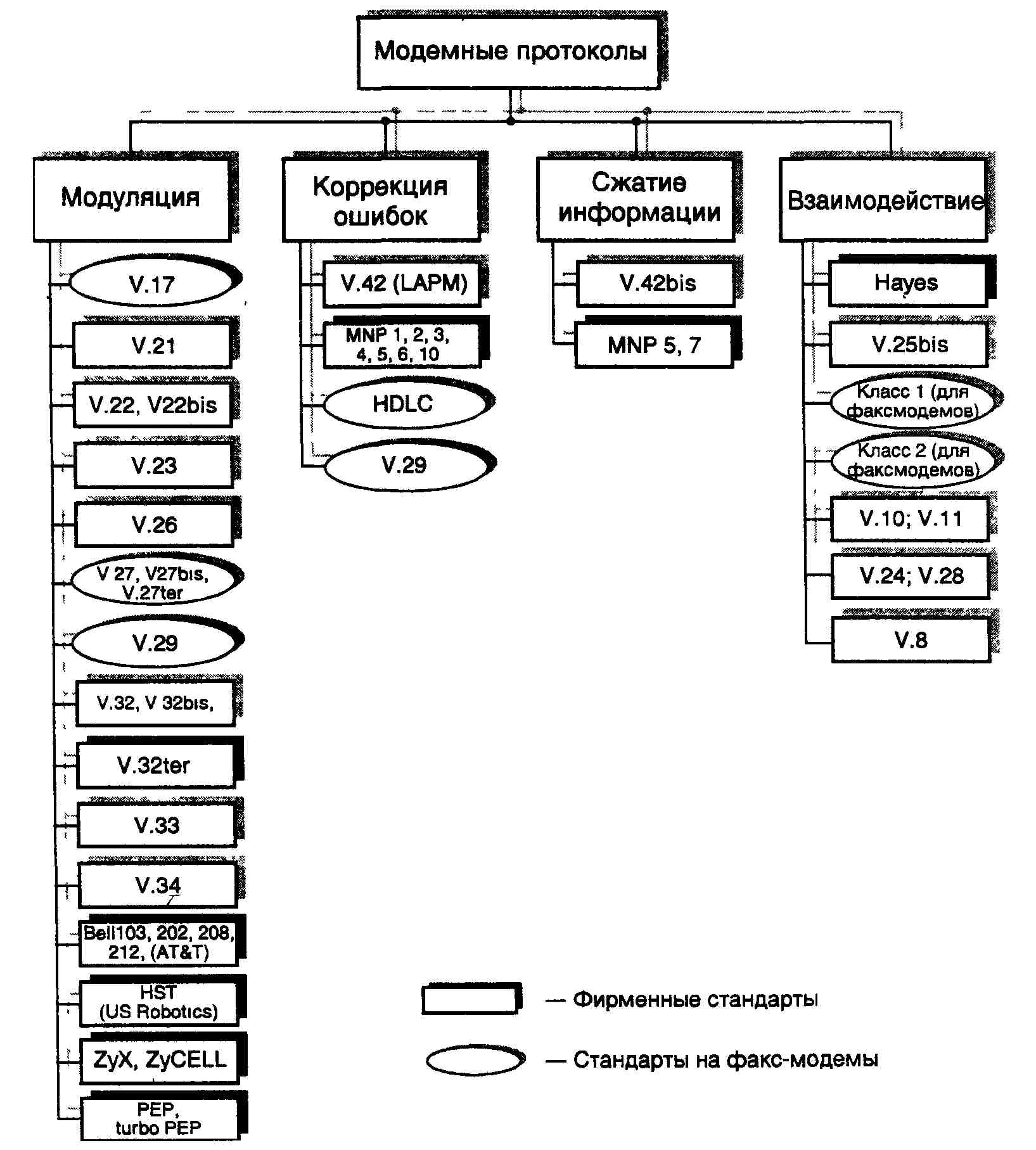
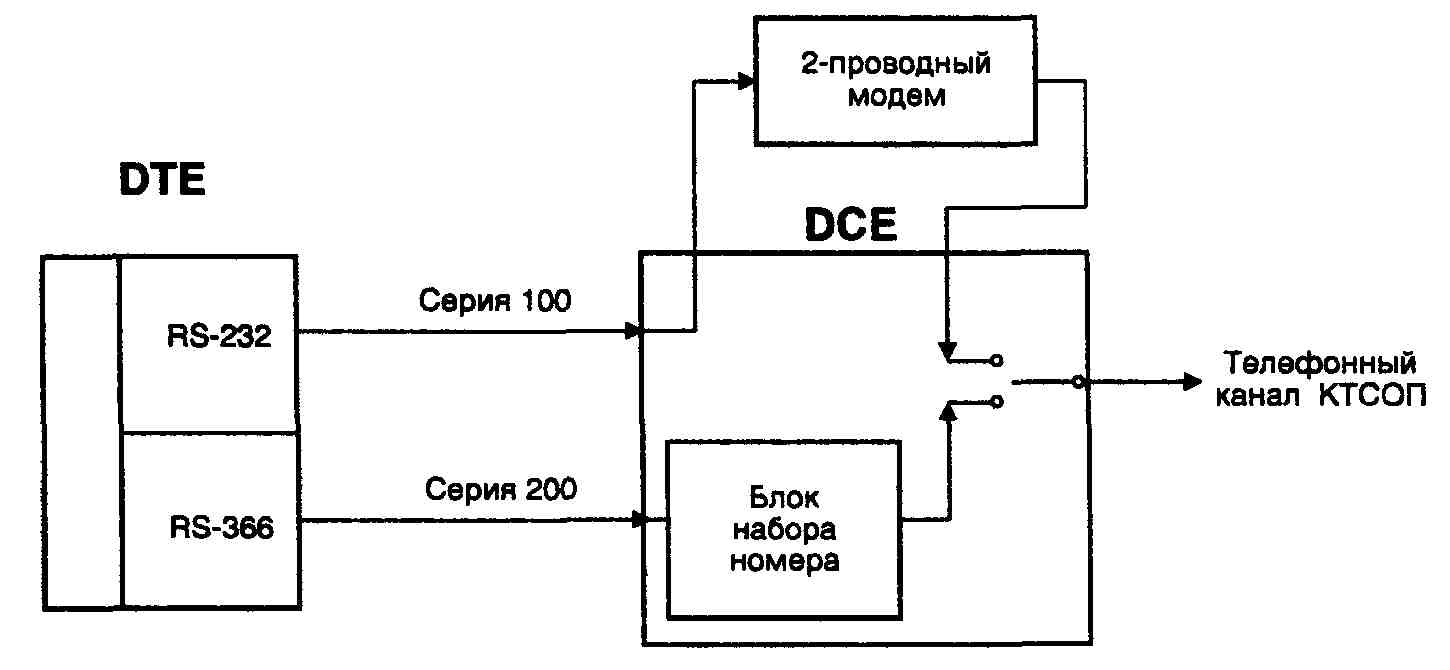
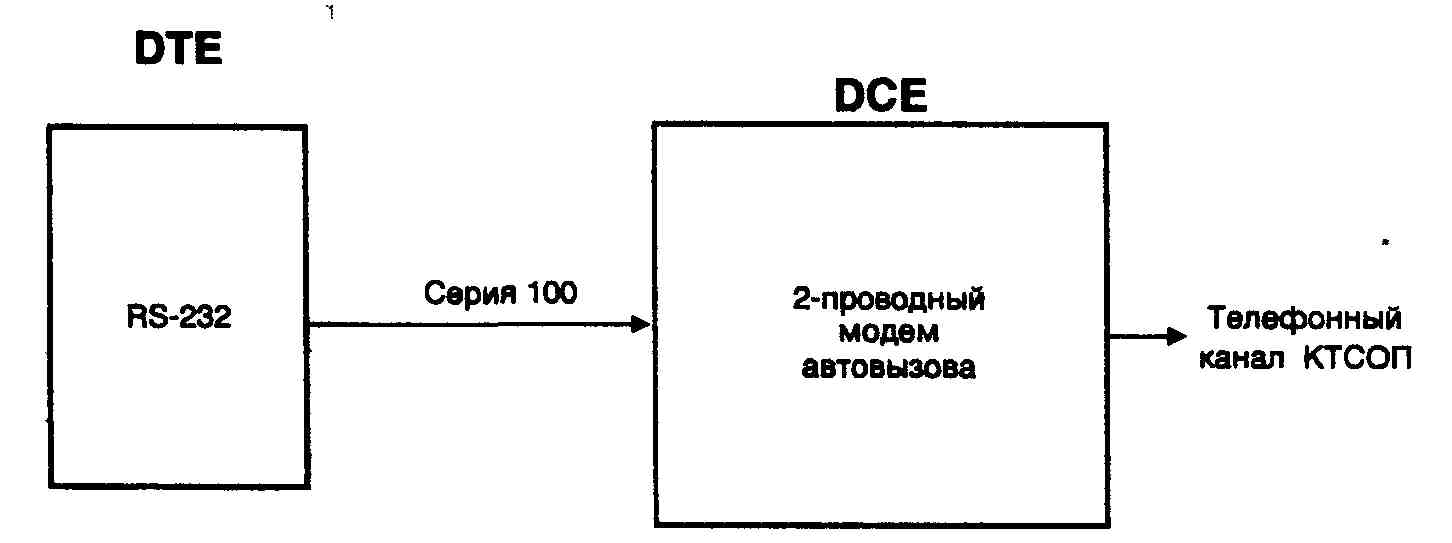
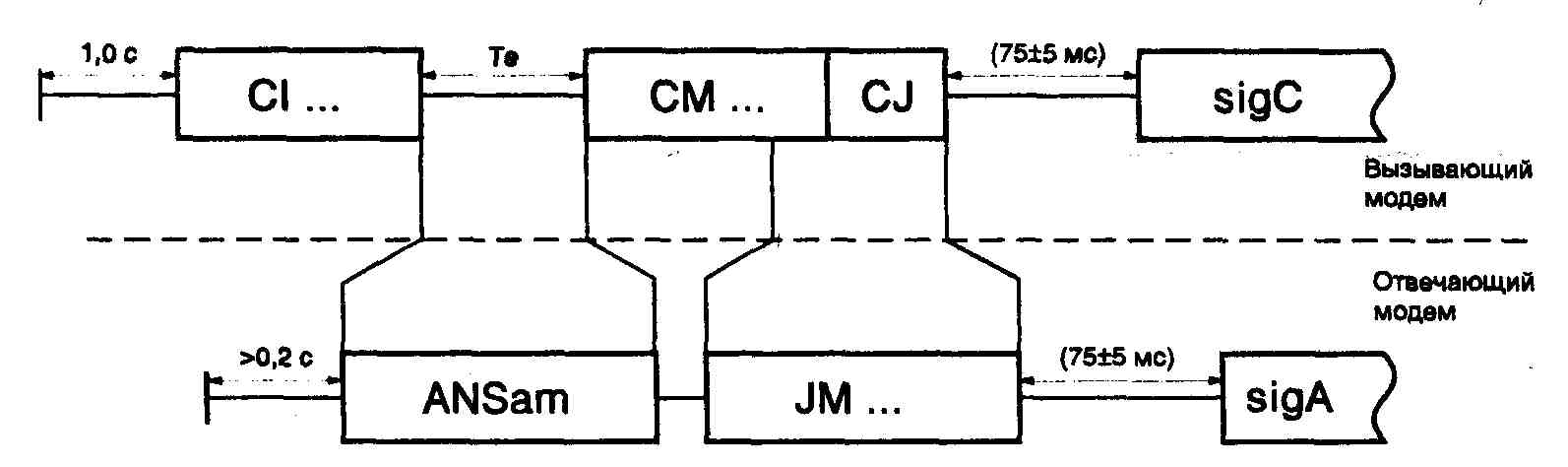
... ITU-T серии V, реализованный в обоих модемах. На этом этапе соединение устанавливается согласно Рекомендациям V.25 и V.8. Если оба модема поддерживают протокол V.34, то они переходят ко второй фазе, в ходе которой производится классификация канала связи. В течение 3 и 4 фазы происходит обучение адаптивного эквалайзера, эхокомпен-сатора и ряда других систем модема. После установления соединения ...
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
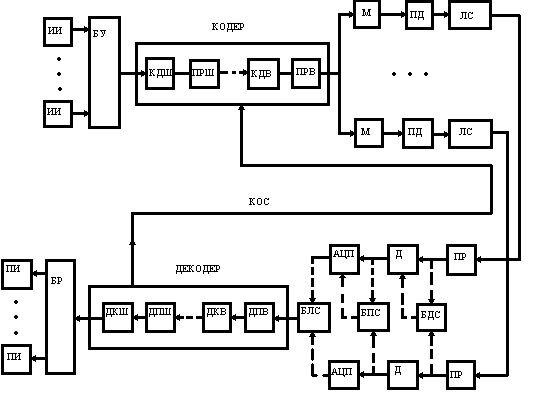
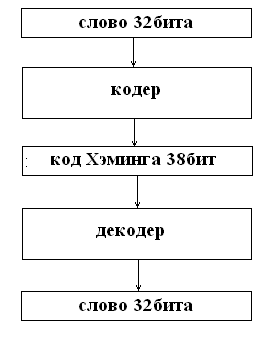
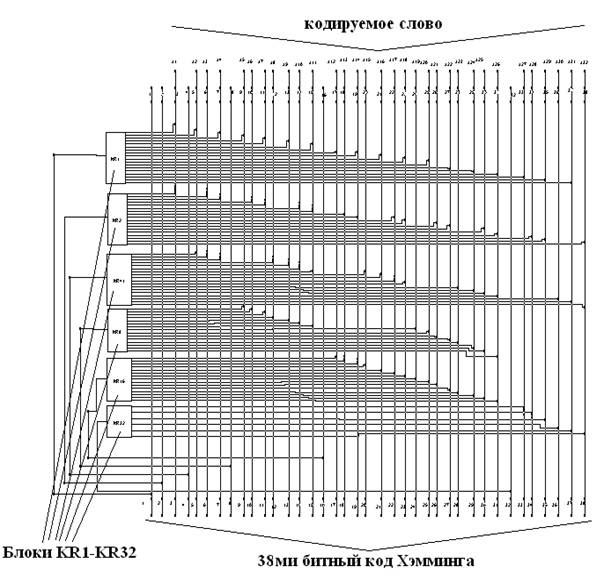
... кодирования можно разработать устройство, которое поможет понять принцип работы метода Хэмминга. Кодер – декодер будем разрабатывать на основе ИМС К555ВЖ1. 2.1 Разработка устройства кодирования информации методом Хемминга Кодер, преобразует 32х битное слово в 38ми разрядный код Хэмминга, после чего слово хранится в памяти или передаётся по шинам и т.д. В процессе передачи или хранения в ...
... , на синфазный и интегрированный каналы по 3, используя то, что человеку более важна информация об интенсивности, нежели о цвете. При “жадном” кодировании, когда используем малое количество бит на пиксел, сразу после декодирования, перед выводом изображения можно провести так называемый anti-aliasing - сгладить резкие цветовые переходы, возникшие из-за малого числа градаций цветовых составляющих. ...
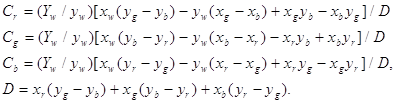
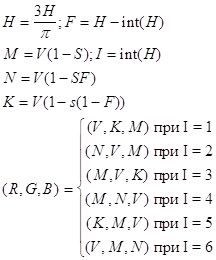
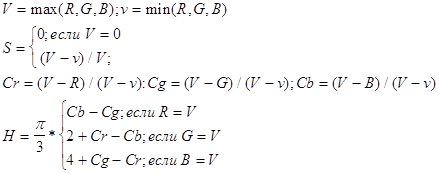
0 комментариев