Навигация
Мм полупроводниковые детекторы регистрируют почти со стопроцентной вероятностью бета-частицы с энергией до 3 МэВ
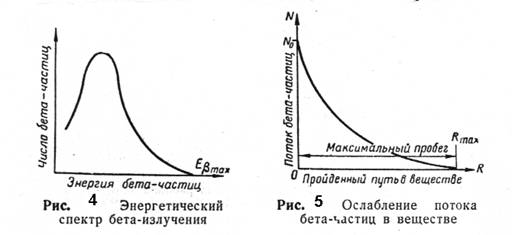
Достоинством пропорциональных счетчиков, сцинтилляционных и полупроводниковых детекторов является возможность получать от этих приборов электрические импульсы, амплитуда которых пропорциональна энергии бета-частицы. Это обстоятельство позволяет регистрировать спектры бета-частиц. Из перечисленных выше приборов наилучшими спектральными характеристиками обладают полупроводниковые детекторы, на которых получают электронные линии с полушириной ~1 кэВ. Более высокой разрешающей способностью (до 1—10 эВ) обладают электростатические и магнитные спектрометры, но эти приборы весьма сложны, дороги и, как правило, обладают малой светосилой (т.е. регистрируют лишь незначительную часть электронов, испущенных источником). В тех опытах, в которых не требуется знание спектрального распределения электронов, для их регистрации используются счетчики Гейгера-Мюллера как наиболее простые и эффективные детекторы. Для измерения спектрального распределения бета-частиц используются сцинтилляционные кристаллы и полупроводниковые детекторы. Из других методов детектирования электронов отметим счетчики, регистрирующие черенковское свечение, возникающее при прохождении быстрых электронов через вещество, однако эти счетчики наиболее эффективны при больших энергиях электронов.
Определение граничной энергии бета-спектра методом поглощения
Знание максимальной энергии бета-излучения необходимо для решения многих научных и практических задач. Во многих важных случаях периоды полураспада оказываются очень короткими и составляют всего несколько минут или даже секунд. При этом часто приходится иметь дело с препаратами малой интенсивности. Поэтому необходимы простые и быстрые способы определения максимальной энергии бета-излучения, не требующие к тому же больших активностей. Одним из таких способов является метод поглощения, которым можно определить максимальную энергию бета-спектра с погрешностью порядка 5—10%. Такая точность часто бывает достаточной при решении прикладных задач. Точнее определить энергию бета-частиц можно с помощью пропорционального счетчика, сцинтилляционного, полупроводникового и магнитного спектрометров.
Принцип метода поглощения заключается в определении пробега электронов в каком-либо веществе.
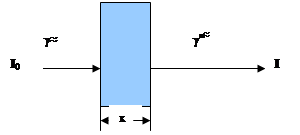
Рассмотрим пучок электронов, падающий нормально на поверхность фильтра (рис. 29). Первоначально быстрые электроны проходят в поглотителе некоторое расстояние приблизительно по прямой линии, теряя небольшие количества энергии и испытывая лишь малые отклонения.
По мере уменьшения энергий электронов их рассеяние становится более 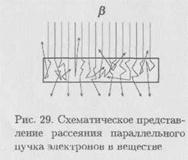 сильным. Угловое распределение электронов в пучке начинает приближаться к гауссову, характерному для многократного рассеяния. В этой области наиболее вероятный угол рассеяния увеличивается пропорционально квадратному корню из пройденной толщины фольги. При дальнейшем рассеянии угловое распределение становится настолько размытым, что нельзя говорить о каком-либо преимущественном направлении движения электронов, и их распространение можно рассматривать как диффузию.
сильным. Угловое распределение электронов в пучке начинает приближаться к гауссову, характерному для многократного рассеяния. В этой области наиболее вероятный угол рассеяния увеличивается пропорционально квадратному корню из пройденной толщины фольги. При дальнейшем рассеянии угловое распределение становится настолько размытым, что нельзя говорить о каком-либо преимущественном направлении движения электронов, и их распространение можно рассматривать как диффузию.
Число электронов, прошедших через фольгу, есть монотонно убывающая функция толщины фольги. Для умеренных толщин уменьшение числа электронов является следствием, главным образом, обратной диффузии электронов, которые отклоняются на углы, превышающие 90°, в результате сложения большого числа отклонений на малые углы. При дальнейшем увеличении толщины фольги уменьшение числа электронов происходит как вследствие рассеяния, так и по причине того, что часть из них тормозится практически до нулевой энергии и, таких образом, выбывает из пучка. Предельная толщина фольги, практически полностью задерживающая первоначально падающие электроны, называется эффективным пробегом электронов. Этот пробег определяется по кривым поглощения.
Так как теоретические расчеты эффективного пробега моноэнергетических электронов в конденсированной среде трудны, приходится обращаться к установлению эмпирического соотношения "пробег — энергия" путем измерения пробега моноэнергетических электронов известной энергии.
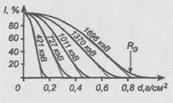
Рис. 4. Кривые поглощения моноэнергетических электронов разных энергий в алюминии.
Однако при этом возникает трудность экспериментального определения пробега по измеренной кривой поглощения. Экспериментально пробег не может быть определен как предельная толщина поглотителя, которую уже не могут пройти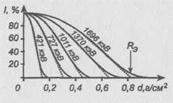 первоначально падающие электроны, так как различные электроны данного пучка рассеиваются или тормозятся по-разному и такая толщина практически не существует.
первоначально падающие электроны, так как различные электроны данного пучка рассеиваются или тормозятся по-разному и такая толщина практически не существует.
На рис. 5 приведены типичные кривые поглощения в алюминии для моноэнергетических электронов различных энергий. По оси абсцисс отложена толщина d алюминиевого фильтра, по оси ординат — интенсивность I пучка электронов, прошедших через фильтр. Каждая кривая имеет после начальной выпуклой части довольно длинную прямолинейную часть, заканчивающуюся некоторым "хвостом". Наиболее воспроизводимой чертой кривых поглощения, снятых при различных условиях эксперимента является точка пересечения линейной части кривой поглощения с осью абсцисс (экстраполированный пробег![]() ,).
,).
Экстраполированный пробег используется для практических целей. Выше 0,8 МэВ связь между пробегом ![]() и энергией электронов может быть выражена линейным соотношением
и энергией электронов может быть выражена линейным соотношением ![]() = А + BE, где А и В — константы.
= А + BE, где А и В — константы.
Кривые поглощения в случае бета-излучения, имеющего непрерывный энергетический спектр, отличаются от кривых поглощения для моноэнергетических электронов более резким, почти экспоненциальным спадом. Такой спад объясняется тем, что в пучке бета-частиц имеются электроны всевозможных энергий, в том числе и очень малых, медленные же электроны поглощаются весьма сильно. Типичная кривая поглощения бета-излучения приведена на рис. 5а. Как видно, конец кривой поглощения подходит к линии фона асимптотически. Такой ход кривой объясняется постепенно уменьшающимся в бета-спектре числом быстрых электронов и относительно слабым поглощением электронов максимальной энергии. По такой кривой поглощения нельзя произвести непосредственное определение пробега.
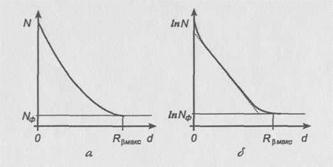
Рис. 5. Типичная кривая поглощения для случая непрерывного бета-спектра (а), (б) – та же кривая в полулогарифмическом масштабе
Для определения пробега целесообразно построить рассматриваемую кривую в полулогарифмическом масштабе (рис. 5б). В этом случае пробег бета-частиц, соответствующий их максимальной энергии, определяется по точке пересечения конца кривой поглощения с линией фона.
Для определения максимальной энергии бета-излучения необходимо иметь кривую "пробег—энергия", такую же, как в случае моноэнергетических электронов. Многие исследователи занимались установлением зависимости между ![]() максимальным пробегом
максимальным пробегом ![]() .
.
Некоторые простые эмпирические соотношения между энергией и максимальным пробегом бета-частиц в алюминии даются уравнениями
Е = 1,39 R0,6, при Е< 0,15 МэВ, (7)
Е = 1,92 R0,725, при 0,15 МэВ< Е< 0,8 МэВ. (8)
Е = 1,85 R + 0,245, при Е> 0,8 МэВ. (9)
В формулах (5.7) (5.9) максимальный пробег R дан в граммах на квадратный сантиметр (г/см2) алюминиевого фильтра, способного практически полностью поглотить бета-частицы с данной граничной энергией.
На рис.42-43 приведена кривая, связывающая пробег бета-частиц с их максимальной энергией.
Непрерывное энергетическое распределение бета-частиц, испускаемых радиоактивными веществами, и рассеяние электронов при прохождении через вещество приводит к тому, что ослабление пучка бета-частиц, идущих от источника к детектору, носит характер, близкий к экспоненциальному закону
![]() (10)
(10)
Экспоненциальный закон хорошо совпадает с экспериментальной кривой в области средних значений толщины поглотителя. В области малых и больших значений наблюдается заметное отступление от экспоненциального закона (см. рис. 5б.) При измерениях удобно пользоваться толщиной слоя половинного поглощения![]() , необходимого для уменьшения вдвое начальной интенсивности бета-излучения. Так как
, необходимого для уменьшения вдвое начальной интенсивности бета-излучения. Так как ![]() и
и![]() , то
, то
![]() (11)
(11)
Коэффициент ослабления ![]() находят по наклону прямолинейного участка кривой поглощения
находят по наклону прямолинейного участка кривой поглощения ![]() , где
, где ![]() угол наклона прямой).
угол наклона прямой).
Связь между толщиной слоя алюминия, ослабляющего излучение в ![]() раз, и верхней границей бета-спектра была тщательно исследована. На с. 94 приводится номограмма, связывающая толщину слоя половинного поглощения с граничной энергией
раз, и верхней границей бета-спектра была тщательно исследована. На с. 94 приводится номограмма, связывающая толщину слоя половинного поглощения с граничной энергией ![]() — спектра.
— спектра.
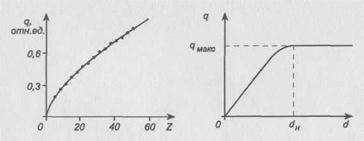
Рис. 6. Зависимость коэффициента обратного рассеяния q от атомного номера 2 отражателя
Рис. 7. Зависимость коэффициента обратного рассеяния от толщины отражателя
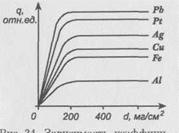
Рис. 8. Зависимость коэффициента обратного рассеяния от толщины отражателя из различных металлов. Излучатель ![]()
Толщина слоя вещества, начиная с которой q не зависит от толщины отражателя, называется толщиной насыщения обратного рассеяния dH.Эта толщина равна примерно 1/5 от максимального пробега бета-частиц данной энергии в данном веществе. Величина q зависит от атомного номера Z и слабо зависит от плотности электронов в веществе. Из рис. 8 видно, что ![]() меньше
меньше ![]() , хотя плотность электронов в платине больше, чем в свинце. Это свидетельствует о том, что рассеяние происходит в основном на атомных ядрах, а не на электронных оболочках атомов.
, хотя плотность электронов в платине больше, чем в свинце. Это свидетельствует о том, что рассеяние происходит в основном на атомных ядрах, а не на электронных оболочках атомов.
На рис. 10 схематически изображено обратное рассеяние бета-частиц при разных толщинах рассеивателя. Следует отметить, что обратное рассеяние бета-частиц в отличие от оптического отражения происходит не только на поверхности рассеивателя, но и в его глубине. На схеме действительная картина обратного рассеяния сильно упрощена: показано рассеяние на один и тот же угол и не учтено поглощение бета-частиц веществом.
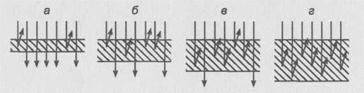
Рис. 10. Отражение бета-частиц в зависимости от толщины образца
При небольшой толщине рассеивателя ![]() большинство электронов проходит сквозь вещество, и лишь небольшое их число рассеивается в обратном направлении. По мере увеличения толщины число обратно рассеянных электронов увеличивается (б, в). Наконец, при d > dH частицы, глубоко проникшие в рассеиватель, уже не выйдут наружу из-за поглощения в нем (г). При дальнейшем увеличении толщины рассеивателя число вышедших из него обратно рассеянных электронов остается постоянным.
большинство электронов проходит сквозь вещество, и лишь небольшое их число рассеивается в обратном направлении. По мере увеличения толщины число обратно рассеянных электронов увеличивается (б, в). Наконец, при d > dH частицы, глубоко проникшие в рассеиватель, уже не выйдут наружу из-за поглощения в нем (г). При дальнейшем увеличении толщины рассеивателя число вышедших из него обратно рассеянных электронов остается постоянным.
Коэффициент обратного рассеяния растет с ростом граничной энергии бета-спектра до энергии 0,6 МэВ, а далее остается практически неизменным. Зависимость коэффициента обратного рассеяния q от максимальной энергии показана на рис. 11.
Явление обратного рассеяния электронов может быть использовано для решения многих прикладных задач:
а) Для определения толщины материалов. В этом случае выгоднее применять источники мягкого бета-излучения. Зависимость коэффициента обратного рассеяния от толщины алюминиевого отражателя для разных бета-источников показана на рис. 12.
б) Для определения толщины покрытий. Эффект обратного рассеяния позволяет измерять толщины покрытия без разрушения изделий и покрытий. Не разрушает изделие микрометрический метод, но он требует жесткого постоянства толщины основания, а также магнитный, но в этом случае покрытие должно обладать магнитными свойствами. Оптическими методами можно определить толщины только прозрачных покрытий. Химический метод связан с разрушением изделия и его точность не превышает 15%. В случае применения эффекта обратного рассеяния атомные номера вещества покрытия и подложки должны различаться, по крайней мере, на две единицы.

Рис.11. Зависимость коэффициента обратного рассеяния от максимальной энергии бета-спектра
Эффект обратного рассеяния позволяет измерять толщины никелевых и хромовых покрытий, покрытий на проволоке и бумаге, светочувствительных слоев и т. д., составов на пленке, лаковых покрытий на металлах, покрытий из драгоценных металлов. При этом все измерения делают бесконтактно, без разрушения изделий и непрерывно.
Обратно-рассеянное бета-излучение чувствительно к составу раствора ионов с высокими атомными номерами (рис. 12). Возможно измерение концентрации одного металла в сплаве с другим. Здесь также необходимо иметь набор эталонов с различной концентрацией компонентов. Поток обратно-рассеянных бета-частиц от смеси веществ ![]() и
и ![]() равен
равен
![]() (14)
(14)
где ![]() и
и ![]() — весовые концентрации компонентов,
— весовые концентрации компонентов, ![]() +
+![]() =1.
=1.
ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ СО СРЕДОЙ
Ионизационное торможение заряженных частиц. При электромагнитном взаимодействии быстрых заряженных частиц с электронами вещества последние переходят в возбужденное состояние; когда они остаются внутри атома, происходит возбуждение атома, и спектр этих состояний имеет дискретный характер; в тех случаях, когда электроны вырываются из атома, их энергия может иметь любые значения, а атом при этом ионизуется. Увеличение энергии электрона происходит за счет кинетической энергии падающей частицы. В обоих случаях для краткости принято говорить, что энергия летящей частицы убывает вследствие ионизационных потерь.
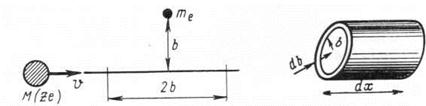
Рассмотрим взаимодействие тяжелой заряженной частицы с электроном. Такая частица ничтожно отклоняется со своего прямолинейного пути и этим отклонением можно пренебречь. Допустим, что частица с зарядом Ze, массой М и скоростью v пролетает на расстоянии b от электрона, где b — прицельный параметр, или параметр удара (рис. 13). Взаимодействие частицы с электроном приведет к тому, что электрон получит импульс в направлении, перпендикулярном к линии полета частицы
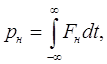
где F – электростатическая сила и ![]() - ее составляющая нормальная к линии полета, а t – время полета
- ее составляющая нормальная к линии полета, а t – время полета
|
|
Импульс же, полученный в продольном направлении ![]() , как легко видеть, равен нулю, так как продольная компонента силы на пути до точки наибольшего сближения и после нее имеет противоположные знаки.
, как легко видеть, равен нулю, так как продольная компонента силы на пути до точки наибольшего сближения и после нее имеет противоположные знаки.
Если считать, что взаимодействие существенно только на некотором отрезке пути 2b,то время пролета определится как ![]() .Кулоновская сила на этом участке по порядку величины
.Кулоновская сила на этом участке по порядку величины ![]() ,поэтому импульс, полученный электроном, может быть записан как
,поэтому импульс, полученный электроном, может быть записан как
![]() (15)
(15)
а переданная электрону энергия
![]() (16)
(16)
Эту энергию в среднем и теряет заряженная частица.
Чтобы учесть все электроны с данным параметром удара, рассмотрим кольцевой цилиндр, ось которого совпадает с траекторией частицы, а боковая поверхность проходит через точку, где находится электрон (рис. 14).
Если число электронов в 1![]()
![]() вещества равно
вещества равно ![]() , то между стенками цилиндров радиусов b и b+db, т. е. в объеме 2πbdb (единичной длины), будет находиться 2πbdb электронов. В результате взаимодействия с ними заряженная частица на длине
, то между стенками цилиндров радиусов b и b+db, т. е. в объеме 2πbdb (единичной длины), будет находиться 2πbdb электронов. В результате взаимодействия с ними заряженная частица на длине ![]() потеряет энергию
потеряет энергию
![]() (17)
(17)
Для получения полных ионизационных потерь нужно проинтегрировать (16) по всем возможным значениям параметра удара от минимального до максимального, что дает
![]() (18)
(18)
Пределы ![]() и
и ![]() выбирают из физических соображений по-разному в релятивистском и нерелятивистском случаях. Так как они входят под знак логарифма, то особая точность в их определении не требуется. При классическом рассмотрении значение
выбирают из физических соображений по-разному в релятивистском и нерелятивистском случаях. Так как они входят под знак логарифма, то особая точность в их определении не требуется. При классическом рассмотрении значение ![]() определяется исходя из максимальной энергии, которая может быть передана электрону в атоме. Такая максимальная энергия передается при лобовом столкновении и равна
определяется исходя из максимальной энергии, которая может быть передана электрону в атоме. Такая максимальная энергия передается при лобовом столкновении и равна ![]() . Подставив это значение в (16), получим
. Подставив это значение в (16), получим
![]()
Учет квантовомеханических эффектов приводит к несколько иному выражению
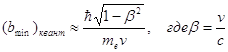
Предел ![]() определяется из энергии связи электрона в атоме, ибо при передаче энергии, меньшей характерной энергии возбуждения атома, возбуждение его вообще не произойдет.
определяется из энергии связи электрона в атоме, ибо при передаче энергии, меньшей характерной энергии возбуждения атома, возбуждение его вообще не произойдет.
В релятивистском случае нужно учесть, что поле падающей частицы сжимается в направлении движения, а величина Ен увеличивается в ![]() раз, где
раз, где ![]() =
= ![]() . Это приводит к тому, что энергия будет передаваться также и более удаленным электронам
. Это приводит к тому, что энергия будет передаваться также и более удаленным электронам
![]()
где ![]() — средний ионизационный потенциал атомов поглощающего вещества.
— средний ионизационный потенциал атомов поглощающего вещества.
Точный подсчет дает окончательно для ионизационных потерь энергии тяжелой частицей
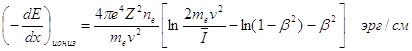 (19)
(19)
Если через вещество проходит не тяжелая частица, а электрон (Z=l), то формула (19) немного изменится, так как сам электрон будет отклоняться в процессе взаимодействия от своего первоначального направления и, кроме того, возникнут так называемые обменные эффекты, имеющие квантовую природу.
В этом случае выражение для удельных потерь будет
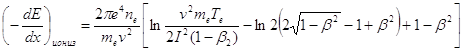 (20)
(20)
где ![]() — кинетическая энергия электрона.
— кинетическая энергия электрона.
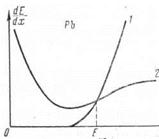
Графически зависимость удельных ионизационных потерь от энергии тяжелых частиц имеет вид, показанный на рис. 15. Рассмотрим физический смысл отдельных членов выражения (19) и поясним ход кривой.
| Рис. 15. Зависимость ионизационных потерь от энергии для тяжелых частиц |
Начальный участок АВ. В этом случае выведенной формулой пользоваться нельзя, так как при малых энергиях импульс налетающей частицы сравним с импульсом орбитального движения электронов. Поэтому траекторию налетающей частицы в процессе взаимодействия нельзя считать прямолинейной, и, кроме того, эта частица не может передать необходимую для возбуждения атома энергию.
Участок ВС. Здесь в основном действует закон ![]() . По мере увеличения скорости частицы сама сила Fн не меняется, но меняется время, взаимодействия, а следовательно, меняется и импульс силы, и передаваемая энергия.
. По мере увеличения скорости частицы сама сила Fн не меняется, но меняется время, взаимодействия, а следовательно, меняется и импульс силы, и передаваемая энергия.
По мере приближения ![]() к
скорости света уменьшение
к
скорости света уменьшение ![]() становится все более медленным, и при скоростях
становится все более медленным, и при скоростях ![]() величина
величина ![]() принимает минимальное значение; далее наблюдается логарифмический рост потерь.
принимает минимальное значение; далее наблюдается логарифмический рост потерь.
Участок CD. Слабый подъем обусловлен эффектом лоренцевского сжатия поля, из-за которого энергия передается все более и более далеким электронам (Ен увеличивается в ![]() раз).
раз).
Участок DE. При дальнейшем увеличении энергии, когда параметр ![]() больше расстояний между атомами, рост потерь ограничивается из-за того, что действующая, на далекий электрон сила уменьшена возникающей под действием поля частицы поляризацией среды. Эта сила в е раз меньше, чем в пустоте (
больше расстояний между атомами, рост потерь ограничивается из-за того, что действующая, на далекий электрон сила уменьшена возникающей под действием поля частицы поляризацией среды. Эта сила в е раз меньше, чем в пустоте (![]() ). На этом участке формула (19) уже несправедлива. С другой стороны, при далеких соударениях возникает новое физическое явление — так называемое излучение Вавилова—Черепкова, приводящее к дополнительным потерям энергии.
). На этом участке формула (19) уже несправедлива. С другой стороны, при далеких соударениях возникает новое физическое явление — так называемое излучение Вавилова—Черепкова, приводящее к дополнительным потерям энергии.
Из формулы (19) можно сделать основной вывод, что удельные потери энергии на ионизацию атомов:
пропорциональны квадрату заряда движущейся частицы (Ze)2,
пропорциональны концентрации электронов в среде ![]() ,
,
являются функцией скорости f(v) и )
не зависят от массы налетающей частицы М, т. е.
![]() (21)
(21)
Так как величина удельных ионизационных потерь зависит от скорости и заряда частицы, то при одной и той же энергии удельные ионизационные потери для электрона будут во много раз меньше, чем для протона или ![]() -частицы. Например, при энергиях порядка нескольких МэВ ионизационные потери электрона примерно в 10 000 раз меньше, чем у
-частицы. Например, при энергиях порядка нескольких МэВ ионизационные потери электрона примерно в 10 000 раз меньше, чем у ![]() -частиц. Именно поэтому у
-частиц. Именно поэтому у ![]() -частиц и электронов такая различная проникающая способность:
-частиц и электронов такая различная проникающая способность: ![]() -частица в воздухе проходит всего лишь несколько сантиметров, прежде чем замедлится до тепловых скоростей, тогда как путь электрона такой же энергии измеряется десятками метров.
-частица в воздухе проходит всего лишь несколько сантиметров, прежде чем замедлится до тепловых скоростей, тогда как путь электрона такой же энергии измеряется десятками метров.
На наблюдении ионизации основан один из самых распространенных методов определения энергии медленных заряженных частиц. Определяется число пар ионов, создаваемых частицей на полном ее пути в веществе, и если известна средняя энергия ![]() , необходимая для образования одной пары ионов, то можно найти полную энергию частицы. Для
, необходимая для образования одной пары ионов, то можно найти полную энергию частицы. Для ![]() -частицы, например, с энергией
-частицы, например, с энергией
1 МэВ в воздухе ![]() = 35 эВ.
= 35 эВ.
Простой вид зависимости ![]() от параметров частицы и среды позволяет легко пересчитывать ионизационные потери, если нужно перейти к другим частицам и средам. Например, если известны потери на ионизацию протона массы mp как функция его энергии, то в области справедливости формулы (5) величина dE/dx может быть найдена при такой же энергии и для любой другой единично заряженной частицы с массой М путем умножения значения потерь энергии на величину отношения масс М/тр.
от параметров частицы и среды позволяет легко пересчитывать ионизационные потери, если нужно перейти к другим частицам и средам. Например, если известны потери на ионизацию протона массы mp как функция его энергии, то в области справедливости формулы (5) величина dE/dx может быть найдена при такой же энергии и для любой другой единично заряженной частицы с массой М путем умножения значения потерь энергии на величину отношения масс М/тр.
Действительно, согласно (17) потери энергии на ионизацию
не зависят от массы частицы, но обратно пропорциональны квадрату ее скорости. Поэтому при равных энергиях они и будут пропорциональны значениям масс.
В релятивистском случае потери энергии, как уже говорилось, пропорциональны логарифму квадрата скорости, и поэтому при одинаковых энергиях различие по массам в 2000 раз меняет ионизационную способность лишь в два раза.
Подобный пересчет может быть сделан и для падающих частиц с другим зарядом.
Пробег заряженных частиц в веществе.
Под пробегом частицы R в каком-нибудь веществе понимается толщина слоя этого вещества, которую может пройти частица с энергией ![]() до полной остановки, если направление ее движения было перпендикулярно поверхности слоя.
до полной остановки, если направление ее движения было перпендикулярно поверхности слоя.
По существу эта величина более или менее определенна лишь для тяжелых частиц, путь которых практически является прямой линией; и по этой причине разброс в величине пробега для частиц одинаковой энергии невелик. У легких частиц, например у электронов малых энергий, вероятность рассеяния велика и поэтому понятие пути и понятие пробега для них не совпадают. По измеренному пробегу частицы в среде можно определять ее энергию, или, зная зависимость величины пробега от энергии, определять массу частицы.
Для данной среды и для частицы с зарядом Ze величина ![]() является функцией только скоростей , а следовательно, у частицы с известной массой функцией только кинетической энергии
является функцией только скоростей , а следовательно, у частицы с известной массой функцией только кинетической энергии
![]()
Зная вид функции ![]() , можно найти и полный пробег частицы
, можно найти и полный пробег частицы
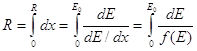 (22)
(22)
Для нерелятивистских энергий ![]() можно записать
можно записать
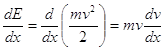 (23)
(23)
![]() (24)
(24)
Подставив (23) и (24) в (22) и произведя интегрирование, получим
![]() (25)
(25)
Из этого соотношения следует, что:
1) при равных скоростях пробеги заряженных частиц в веществе пропорциональны массам этих частиц и обратно пропорциональны квадратам зарядов:
![]()
2) при равных энергиях частиц их пробеги обратно пропорциональны массам:
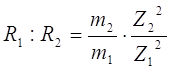
Пробеги заряженных частиц часто выражают в г/см2.
![]()
и пользуются выражением удельных потерь в форме:
![]()
Измерять пробеги в г/см2 удобно, потому что удельные ионизационные потери в легких веществах, рассчитанные на г/см2, одинаковы в разных средах. Действительно, мы видели, что ![]() и, следовательно,
и, следовательно,
![]()
![]()
Однако число электронов, содержащихся в 1 см3 вещества, равно
![]()
где N0 — число Авогадро, А — атомный вес вещества.
Так как у легких элементов ![]() , то в слое любого легкого вещества толщиной 1 г/см2 будет содержаться примерно N0/2 электронов:
, то в слое любого легкого вещества толщиной 1 г/см2 будет содержаться примерно N0/2 электронов:
![]() ,
,
а это означает, что
![]()
Для однозарядных релятивистских частиц
![]() (26)
(26)
и слабо убывает с ростом Z вещества.
На основании формулы для пробега частиц (25), примененной к однородному пучку, который проходит слой поглотителя без рассеяния, можно построить зависимость числа частиц, прошедших через поглотитель, от толщины слоя. Эта кривая изображена на рис. 54. Для монохроматического пучка ![]() -частиц она удовлетворительно совпадает с экспериментом (пунктир).
-частиц она удовлетворительно совпадает с экспериментом (пунктир).
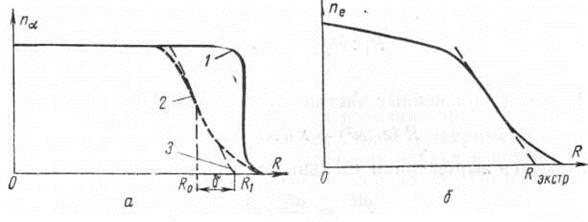
Рис. 16. Зависимость числа моноэнергетических частиц, прошедших поглотитель, от его толщины: а — а-частиц; б — электронов
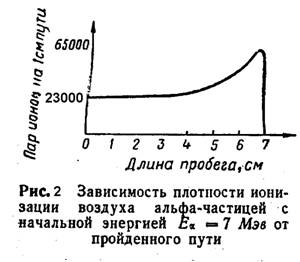
Конечный участок экспериментальной кривой не вертикален, а имеет небольшой наклон вследствие статистического характера процесса потери энергии. Частицы теряют свою энергию в очень большом, но конечном числе отдельных актов. Флуктуации подвержено как число таких актов на единицу длины, так и потери энергии в каждом отдельном акте. В соответствии с этим и пробеги ![]() -частиц испытывают статистические флуктуации. Однако величина разброса пробегов незначительна и составляет приблизительно 1% от полного пробега для
-частиц испытывают статистические флуктуации. Однако величина разброса пробегов незначительна и составляет приблизительно 1% от полного пробега для ![]() -частиц с энергией 5 Мэв (масштаб на рис. 4, а не соблюден).
-частиц с энергией 5 Мэв (масштаб на рис. 4, а не соблюден).
Поэтому по пробегу ![]() -частицы можно с хорошей степенью точности определять их энергию. Электроны же испытывают в веществе многократное рассеяние, направление их движения часто меняется и только в наиболее благоприятных случаях электроны проходят максимальное расстояние в поглотителе в направлении, перпендикулярном к его поверхности. Кривая поглощения колли-мированного пучка моноэнергетических электродов имеет вид, отличный от аналогичной кривой для
-частицы можно с хорошей степенью точности определять их энергию. Электроны же испытывают в веществе многократное рассеяние, направление их движения часто меняется и только в наиболее благоприятных случаях электроны проходят максимальное расстояние в поглотителе в направлении, перпендикулярном к его поверхности. Кривая поглощения колли-мированного пучка моноэнергетических электродов имеет вид, отличный от аналогичной кривой для ![]() -частиц (рис. 16,б). Поэтому энергию электронов нельзя определять по пробегу, а надо измерять полную ионизацию, произведенную ими в веществе.
-частиц (рис. 16,б). Поэтому энергию электронов нельзя определять по пробегу, а надо измерять полную ионизацию, произведенную ими в веществе.
Ядерное взаимодействие
Потери энергии за счет ядерного взаимодействия: рассеяния на ядерных силах, ядерных реакций — имеют большое значение только для сильновзаимодействующих (ядерноактивных) частиц, например ![]() -мезонов и протонов высокой энергии,
-мезонов и протонов высокой энергии, ![]() и
и ![]() -излучение, возникающее при радиоактивном распаде практически не испытывает ядерных взаимодействий.
-излучение, возникающее при радиоактивном распаде практически не испытывает ядерных взаимодействий.
Поскольку ядерные силы короткодействующие, частица должна приблизиться к ядру на расстояние порядка радиуса ядра R~1012 см. Характерный же параметр удара для ионизационных потерь ![]() см. Вероятность тех или иных физических явлений, определяется эффективным сечением
см. Вероятность тех или иных физических явлений, определяется эффективным сечением ![]() . Поэтому для взаимодействий, обусловленных ядерными силами,
. Поэтому для взаимодействий, обусловленных ядерными силами, ![]() , а для ионизационных потерь
, а для ионизационных потерь ![]() ,а их отношение
,а их отношение ![]() , т. е. только в одном случае из 107—108 столкновений происходит ядерная реакция. Таким образом, ядерная реакция — событие очень редкое даже для частиц высокой энергии.
, т. е. только в одном случае из 107—108 столкновений происходит ядерная реакция. Таким образом, ядерная реакция — событие очень редкое даже для частиц высокой энергии.
Однако при каждой ядерной реакции частица теряет значительную часть своей энергии, в то аремя как при столкновении с атомной оболочкой она теряет всего ![]() и таким образом ядерноактивные частицы при прохождении через среду эффективно выбывают из коллимированного пучка за счет процессов поглощения и рассеяния. Подробнее различные ядерные реакции будут рассмотрены в соответствующем разделе.
и таким образом ядерноактивные частицы при прохождении через среду эффективно выбывают из коллимированного пучка за счет процессов поглощения и рассеяния. Подробнее различные ядерные реакции будут рассмотрены в соответствующем разделе.
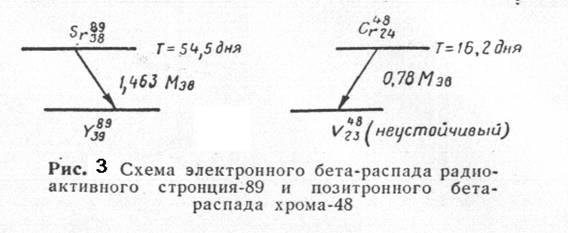
Электроны, испускаемые ядрами при радиоактивном называются - минус - или просто - частицами. При радиоактивном распаде также могут испускаться - плюс - частицы, масса которых равна массе электрона, заряд их равен заряду электрона, но положителен. Эти частицы называются позитронами. Взаимодействие с веществом электронов и позитронов имеет много общего, поэтому их можно рассматривать совместно.
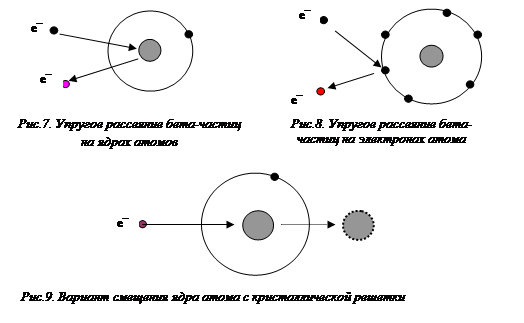
При движении через вещество быстрые - частицы взаимодействуют с электрическими оболочками атомов и атомными ядрами среды. Взаимодействие осуществляется электрическими (кулоновскими) силами. Основными типами взаимодействия являются упругое рассеяние, неупругое рассеяние и радиационное торможение.
В результате упругого рассеяния - частица после столкновения с атомом изменяет направление и скорость движения, но суммарная кинетическая энергия - частицы и атома не меняется. Упругое рассеяние - частиц на атомных электронах в z раз менее вероятно, чем на атомных ядрах (z – заряд ядра), и осуществляется при относительно низких энергиях - частиц (E0 < 0,5 МэВ). При малых энергиях угловое распределение рассеянных - частиц описывается уравнением Резерфорда (5.1), которое справедливо для однократного рассеяния электронов, то есть для тонких слоев вещества.
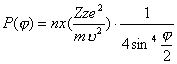 (5.1)
(5.1)
где P() - относительное число частиц, рассеянны: в единицу телесного угла в направлении, составляющем угол с направлением пучка - частиц; n – число атомов в 1 куб. см; x - толщина рассеивающей пластинки; Z - заряд ядер рассеивающей среды; z, m, - заряд, масса и скорость рассеиваемых частиц.
С увеличением толщины поглощающего слоя рассеяние переходит в гауссово, а при значительных толщинах становится диффузным и не зависит от толщины.
Полное сечение упругого ядерного рассеяния ![]() .
.
Эффективное сечение рассеяния бета - частиц на атомных электронах пропорционально ![]() .
.
Таким образом
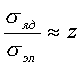
Для водорода (Z=0) вероятности этих процессов одинаковы, а для тяжелых ядер имеет место преимущественно ядерное рассеяние.
При неупругих соударениях за счет кинетической энергии бета - частиц происходит возбуждение или ионизация атомов. Величина потери энергии на единице пути dE/dx (удельные ионизационные потери) на ионизацию и возбуждение описываются уравнением,
![]() (5.2)
(5.2)
где E - кинетическая энергия, n - число атомов в единице объема, Z - заряд ядра поглотителя, e - заряд электрона, B - коэффициент торможения; z, m, - заряд, масса, скорость бета - частицы.
Из уравнения (5.2) следует, что с ростом энергии бета - частицы ионизационные потери уменьшаются:
![]()
Электроны, которые освобождаются в процессе первичной ионизации, часто обладают большими энергиями и производят дополнительную, или вторичную ионизацию. Полная ионизация представляет собой сумму первичной и вторичной ионизации.
Ионизационные потери энергии сопровождаются характеристическим рентгеновским излучением возникающим при заполнении свободных уровней электронами.
При движении быстрых бета - частиц через поглощающую среду существенную роль играют потери на излучение. Взаимодействие бета - частиц с кулоновским полем атомных ядер приводит к торможению бета - частиц с испусканием тормозного излучения. В соответствии с классической электродинамикой заряд, испытывающий ускорение a, излучает энергию
![]()
где e - заряд частицы, c - скорость электромагнитных волн.
Вследствие своей малой массы бета - частицы в кулоновском поле ядра могут испытывать большое ускорение, так как ускорение пропорционально заряду ядра Z, деленному на массу электрона.
Из теории следует, что величина удельных потерь, обусловленных излучением, определяется соотношением:
![]() (5.3)
(5.3)
где E – энергия бета – частиц, Фрад - эффективное поперечное сечение для радиационных потерь, n - число атомов в единице объема.
Для медленных электронов ( / c << 1)
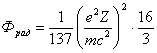
Для быстрых электронов ( / c 1)

Таким образом, радиационные потери растут с ростом энергии бета - частиц E, а для быстрых бета - частиц - несколько быстрее. Кроме того, они пропорциональны Z 2.
Отношение радиационных потерь энергии к ионизационным потерям равно
Энергия, при которой ионизационные потери равны радиационным, называется критической. Величина критической энергии для бета - частиц определяется приближенно соотношением:
![]()
Полные потери энергии бета - частицами при энергиях ниже критической определяется, в основном, ионизационными потерями, а при энергиях выше - критической преобладают радиационные потери.
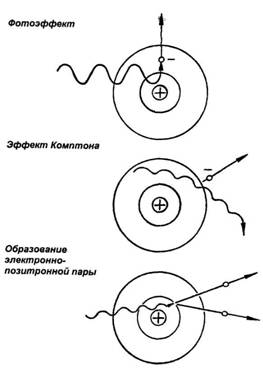
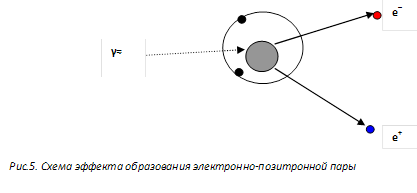
Замедленный позитрон соединяется с электроном, и пара аннигилирует. Энергия покоя двух частиц передается двум возникающим фотонам. Эти фотоны, представляющие собой так называемое аннигиляционное излучение, имеют энергию mc2 = 0,511 МэВ каждый и движутся в противоположных направлениях. Аннигиляция не является обычным этапом в судьбе электрона, так как количество позитронов, необходимых для этого процесса, обычно мало по сравнению с количеством электронов. Замедляясь, бета – минус - частица становится одним из электронов вещества.
Длина пробега заряженной частицы равна пути, на котором первичная кинетическая энергия частицы растрачивается за счет взаимодействия со средой, т.е.
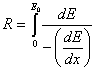 (5.4)
(5.4)
Пробеги измеряются либо в единицах длины, либо в г / см2 (мг / см2), причем
![]()
Отсюда следует, что пробег частицы есть функция ее кинетической энергии, поэтому измерения длин пробегов частиц позволяет найти их кинетические энергии. Отметим, что определение истинной длины пути частицы в веществе по толщине поглощающего слоя возможно только для тяжелых частиц, которые не испытывают заметного рассеяния в кулоновских полях ядер. Для бета - частиц, в отличие от тяжелых частиц, траектория в веществе не является прямолинейной. Бета – частицы проходят в веществе довольно извилистые пути, а величины пробегов моноэнергетических электронов сильно отличаются между собой. Бета – частица на своем пути испытывает множество актов рассеяния на атомах вещества. Этим обусловлены изломы на его пути. Рассеяние может происходить при соударении с орбитальными электронами или с ядрами вещества поглотителя.
Число бета - частиц, прошедших поглотитель заданной толщины является постепенно уменьшающейся функцией толщины поглотителя. Максимальная толщина поглотителя, поглощающая практически все падающие на нее бета - частицы, характеризует так называемый практический (или эффективный) пробег. Практический пробег является функцией максимальной энергии бета - излучения E0.
Детальное изучение энергетического спектра бета - излучения производят спектрометрическими методам, (магнитный бета - спектрометр, кремниевый полупроводниковый детектор и т.д.), требующими сложной аппаратуры. В тех случаях, когда требуется определить максимальную энергию бета - спектра с точностью, не превышающей 5 %, используют метод поглощения.
Цель настоящей работы состоит в определении максимальной энергии бета - излучения методом поглощения.
Для определения максимальной энергии бета - частиц методом поглощения снимают кривую поглощения бета - излучения в веществе (как правило, в алюминии), то есть находит, пользуясь набором тонких фольг, зависимость интенсивности бета - частиц I, прошедших через фольгу, от толщины поглотителя. При малых толщинах поглотителя поглощение бета - излучения в веществе подчиняется в первом приближении экспоненциальному закону, но точно этому закону не следует, и практический пробег бета - частиц составляет для различных элементов пяти – десяти - кратную величину толщины слоя половинного поглощения.
Результаты измерения наносят на полулогарифмический график. По оси абсцисс наносят толщину слоя, а по оси ординат – логарифмы интенсивности излучения. В случае изотопа с простым бета – спектром (бета – частицы имеющие одну максимальную энергию) и испускающего еще и гамма – излучение получается кривая, показанная на рис. 5.1. Практический пробег R находится путем экстраполирования кривой поглощения к уровню фона от гамма – излучения, или применяют метод сравнения Физера, который позволяет определить пробег в каком – либо веществе путем сравнения кривой поглощения в этом веществе с кривой поглощения в веществе с известным пробегом.
Радиационное торможение электронов (тормозное  излучение).
излучение).
|
Согласно классической теории любая заряженная частица, Рис. 17. движущаяся с ускорением,
должна излучать электромагнитные волны. Допустим, что частица с зарядом е, массой т и скоростью ![]() движется мимо ядра, обладающего массой М
движется мимо ядра, обладающего массой М![]() и зарядом Zяe. При рассеянии кулоновским центром частица претерпевает отклонение (рис. 17) и, следовательно получает ускорение. В соответствии с классической электродинамикой заряд, испытывающий ускорение
и зарядом Zяe. При рассеянии кулоновским центром частица претерпевает отклонение (рис. 17) и, следовательно получает ускорение. В соответствии с классической электродинамикой заряд, испытывающий ускорение ![]() в течение времени
в течение времени ![]() излучает энергию
излучает энергию
![]()
Поскольку ![]() , то
, то ![]() . Таким образом, радиационные потери энергии наиболее существенны у самых легких частиц – электронов; для протонов, например, при той же энергии эффект уже в
. Таким образом, радиационные потери энергии наиболее существенны у самых легких частиц – электронов; для протонов, например, при той же энергии эффект уже в ![]() раз меньше.
раз меньше.
Релятивистский квантовый расчет, проведенный Бете и Гайтлером, позволяет найти потери энергии электроном на тормозное излучение
![]() (27)
(27)
где ![]() - так называемая постоянная тонкой структуры;
- так называемая постоянная тонкой структуры; ![]() - классический радиус электрона;
п — число атомов в см3 вещества; Е—полная энергия излучающего электрона.
- классический радиус электрона;
п — число атомов в см3 вещества; Е—полная энергия излучающего электрона.
Для того чтобы удобнее было сравнивать потери энергии на излучение в различных веществах, вводится так называемая «радиационная» единица длины ![]() :
:
| (28) |
![]()
другими словами, весь коэффициент при Е, имеющий размерность ![]() обозначается
обозначается
![]() . Тогда
. Тогда ![]() и, если измерять толщину вещества в этих единицах, то
и, если измерять толщину вещества в этих единицах, то
![]() и
и ![]() (29)
(29)
Отсюда видно, что потери энергии электроном на одной t - единице длины не зависят от вещества (но сама эта единица для разных веществ, конечно, различна). Интегрируя (29), получаем простой закон изменения энергии частицы
![]() (30)
(30)
где Ео— начальная энергия электрона. Следовательно, t -единица — это та длина, на которой энергия частицы уменьшается в е раз. Для воздуха, например, ![]() = 300 м, для свинца
= 300 м, для свинца ![]() = 0,5 см.
= 0,5 см.
Как видно из выражения (13), потери энергии на тормозное излучение подчиняются иным закономерностям, чем потери энергии вследствие неупругих соударений:
1) до энергий порядка тос2 они постоянны, а затем возрастают пропорционально Е и при достаточно больших энергиях
|
|
|
2) потери на излучение пропорциональны квадрату заряда ядра, поэтому для тяжелых элементов они более существенны, чем для легких.
Если сравнить формулы для потерь энергии электронов на ионизацию и тормозное излучение (19) и (27), то можно найти отношение этих потерь:
![]()
Отсюда следует, что в воздухе, например, потери на излучение становятся сравнимыми с потерями на ионизацию при Ео = 80 МэВ. Для свинца это наступает уже при Ео = 6 МэВ (энергия, при которой потери на излучение становятся равными потерям на ионизацию, называется критической энергией Eкр) (рис. 18).
Поэтому относительный .вклад различных потерь энергии существенно зависит не только от вещества, массы, но и от энергии частицы.
Литература
1. Г.Бете, Ю.Дж.Ашкин Прохождение ![]() — частиц через вещество. —В кн.: экспериментальная ядерная физика. Под ред. Э. Сегре. М.. 1955.
— частиц через вещество. —В кн.: экспериментальная ядерная физика. Под ред. Э. Сегре. М.. 1955.
2. Г.Кноп, В.Пауль Альфа-, бета-, гамма-спектроскопия. Под ред. К. Зигбана. Т. 1. М., 1969.
3. Н.Бор Прохождение атомных частиц через вещество. М., 1950.
4. Н.И.Штейнбок Измерение толщины покрытий методом рассеяния бета-излучения. — Применение радиоактивных излучателей в измерительной технике, 1960.
5. Ц.С. Ву, С.А.Мошковский Бета-распад. М., 1970
Похожие работы
... β Свинец-210 22,3 лет β Висмут-210 5,01 суток β Полоний-210 138,4 суток Свинец-206 стабильный 4. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЙ С ВЕЩЕСТВОМ Для регистрации радиоактивности и мер защиты от ядерных излучений, необходимо знать за счет каких процессов теряется энергия излучения, проходя через вещество; какова ионизирующая способность различных видов излучения. В основном ...
... .12 Форма импульсов напряжения на аноде счетчика Мертвое время имеет величину порядка 10ˉ5—10ˉ3 сек. в зависимости от типа и режима работы счетчика. Мертвое время ограничивает максимальную интенсивность излучений, которую способен регистрировать счетчик без существенных ошибок, т. е. определяет его разрешающую способность — максимальный счет радиоактивных частиц в единицу времени. ...
... алюминии Энергия альфа частиц Еα, МэВ Воздух, см Биологическая ткань, мкм Алюминий, мкм 4,0 2,5 31 16 4,5 3,0 37 20 5,0 3,5 43 23 6,0 4,6 56 30 7,0 5,9 72 38 8,0 7,4 91 48 9,0 8,9 110 58 10 10,6 130 69 Характеристики ионизирующих излучений. Единицы измерения Для установления закономерностей распространения и поглощения ионизирующих излучений ...
... элементарных частиц — это своего рода постулат, и проверка его справедливости — одна из важнейших задач физики. От электрона до нейтрино Электрон Исторически первой открытой элементарной частицей был электрон — носитель отрицательного элементарного электрического заряда в атомах. Это самая «старая» элементарная частица. В идейном плане он вошел в физику в 1881 г., когда Гельмгольц в ...

0 комментариев