1. Активность
Рассмотренные нами соотношения для идеальных растворов не могут быть непосредственно использованы для вычисления равновесия, в котором участвуют реальные растворы, в частности в реальных растворах не выполняется один из основных законов химии – з. действия масс. При подставлении в выражения для константы равновесия концентрации реагирующих веществ константа равновесия оказывается не постоянно зависящей от концентрации. В случае идеальных растворов из измерения одного из свойств (давление пара) можно рассчитать все другие свойства. Желательно сохранить такую возможность для реальных растворов. Решение было предложено Льюисом, который ввел в теорию растворов так называемые т/д активности в качаестве ф-ии, связывающей свойства равствора друг с другом и заменил концентрацию в реальных растворах. Подставляя т/д активность в место концентрации, в т/д уравнение, полученное для идеальных растворов делает последнее пригодным и для реальных растворов. Т.о. активностью называется величина, подставляя которую вместо концентрации в т/д уравнение делает последнее применимым для реальных растворов, а – активность. После введения активного хим. потенциала i определяется соотношением ![]() Bb+dD↔Mm+rR. Константу равновесия определяет соотношение
Bb+dD↔Mm+rR. Константу равновесия определяет соотношение ![]() . З. распределения, если раствор 3-го вещества нельзя считать идеальным
. З. распределения, если раствор 3-го вещества нельзя считать идеальным ![]() . Активность должна быть введена таким образом чтобы в идеальных растворах она совпадала с концентрацией, а в реальных растворах она должна характеризовать отклонение их от идеальных. По Льюису активность выражается соотношением давление пара данного компонента над реальным раствором к давлению пара этого компонента в некотором стандартном состоянии
. Активность должна быть введена таким образом чтобы в идеальных растворах она совпадала с концентрацией, а в реальных растворах она должна характеризовать отклонение их от идеальных. По Льюису активность выражается соотношением давление пара данного компонента над реальным раствором к давлению пара этого компонента в некотором стандартном состоянии ![]() . Для растворимости в водных растворах для всех компонентов летучих жидких смесей. В начале стандартного состояния берут состояние компонентов в чистом виде и тогда при данной температуре
. Для растворимости в водных растворах для всех компонентов летучих жидких смесей. В начале стандартного состояния берут состояние компонентов в чистом виде и тогда при данной температуре ![]()
![]() . В совершенном растворе соотношение
. В совершенном растворе соотношение ![]() => в идеальном растворе активность = концентрации
=> в идеальном растворе активность = концентрации ![]() , в реальном растворе
, в реальном растворе ![]() . Степень отклонения активности и концентрации определяется величиной коэффициента активности
. Степень отклонения активности и концентрации определяется величиной коэффициента активности ![]() . В идеальном растворе
. В идеальном растворе ![]() , в реальном растворе может быть > и < 1. В разбавленных растворах для растворителя выполняется закона Рауля, а для растворов вещества з. Генри
, в реальном растворе может быть > и < 1. В разбавленных растворах для растворителя выполняется закона Рауля, а для растворов вещества з. Генри ![]() . Для растворённого вещества стандартное состояние должно быть сделано таким образом, чтобы в растворе любой концентрации соблюдался закон Генри
. Для растворённого вещества стандартное состояние должно быть сделано таким образом, чтобы в растворе любой концентрации соблюдался закон Генри ![]() ,
, ![]()
![]() .
.
Связи м/у активностями компонентов
Уравнение Дюгема-Маргулиса:
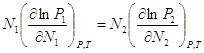 (1). Если раствор является близким к совершенному, то
(1). Если раствор является близким к совершенному, то ![]() , а
, а ![]() .
. ![]() ,
, ![]() . Продифиринцируем (
. Продифиринцируем (![]() и
и ![]() =const)
=const) 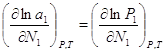 (2),
(2), 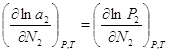 (3). Подставим
(3). Подставим 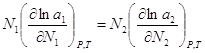 (4). Уравнение (4) может быть обобщено на раствор, содержащий несколько компонентов:
(4). Уравнение (4) может быть обобщено на раствор, содержащий несколько компонентов: 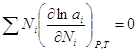 . Если раствор близок к разбавленному
. Если раствор близок к разбавленному ![]() для растворённого вещ-ва
для растворённого вещ-ва ![]() . Повторяя действие, что и здесь справедливо уравнение (4). Для бинарного раствора уравнение (4) имеет вид:
. Повторяя действие, что и здесь справедливо уравнение (4). Для бинарного раствора уравнение (4) имеет вид: ![]() ,
, 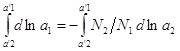 ,
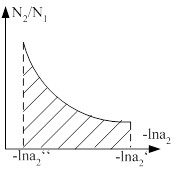
, 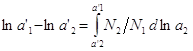 . Если известна зависимость активности второго компонента от концентрации, а так же активность первого компонента для какой либо концентрации, то можно активность компонента для другой концентрации. Зная
. Если известна зависимость активности второго компонента от концентрации, а так же активность первого компонента для какой либо концентрации, то можно активность компонента для другой концентрации. Зная ![]() , можно подсчитать
, можно подсчитать ![]() .
.
Методы определения активности
1) Определение активности по давлению пара, если компонент летучий; например, раствор олово-цинк близок к совершенному. Давление пара при 957К ![]() , а давление пара над сплавом олово-цинк, в котором молярная доля цинка 0,226, составляет
, а давление пара над сплавом олово-цинк, в котором молярная доля цинка 0,226, составляет ![]() . По определению,
. По определению, ![]() , а для летучего компонента
, а для летучего компонента ![]() . Коэффициент активности
. Коэффициент активности ![]()
2) Определение активности на основе закона распределения. В реальных растворах коэффициент распределения рассчитывается по формуле: ![]() , где
, где ![]() и
и ![]() - активности распределяющегося вещества 1-ой и 2-ой фазы. При бесконечном разбавлении, когда количество введенного 3-го компонента невелико, активности равны соответствующим концентрациям, определяя которые, вычисляют к.
- активности распределяющегося вещества 1-ой и 2-ой фазы. При бесконечном разбавлении, когда количество введенного 3-го компонента невелико, активности равны соответствующим концентрациям, определяя которые, вычисляют к. ![]() . Если константа распределения велика, то при увеличении общего количества введенного 3-го компонента 2-й раствор может оставаться идеальным вплоть до насыщения и тогда закон распределения может быть представлен в виде:
. Если константа распределения велика, то при увеличении общего количества введенного 3-го компонента 2-й раствор может оставаться идеальным вплоть до насыщения и тогда закон распределения может быть представлен в виде: ![]() . Определяя С2 и зная константу, рассчитывают а1 , а1=КС2 – активность 3-го компонента в 1-ом растворе.
. Определяя С2 и зная константу, рассчитывают а1 , а1=КС2 – активность 3-го компонента в 1-ом растворе.
Существуют и другие методы определения активности, например, криоскопические. Активность определяется по измеренному понижению температуры замерзания раствора по сравнению с чистым растворителем: ![]() . Активность можно определить из изучения химического равновесия, вычисляя Кр.
. Активность можно определить из изучения химического равновесия, вычисляя Кр.
3) Активность можно вычислить из электрохимических измерений. Например, по формуле Нернста для металлического электрода в растворе своей соли: ![]() , где:
, где: ![]() - стандартный электродный потенциал;
- стандартный электродный потенциал; ![]() - потенциал электронов в растворе, измеряемый существующими методами. Зная
- потенциал электронов в растворе, измеряемый существующими методами. Зная ![]() и
и ![]() рассчитываем а.
рассчитываем а.
Необратимые реакции
Для реакции первого порядка ![]() , где С – концентрация реагирующего исходного вещества. С другой стороны,
, где С – концентрация реагирующего исходного вещества. С другой стороны, ![]() .
.
![]() ;
;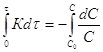 ;
;![]() ;
;![]() (2)
(2)
Из (2) следует, что константа скорости реакции первого порядка не зависит от способа выражения концентрации и имеет размерность ![]() :
:
![]() (3)
(3)
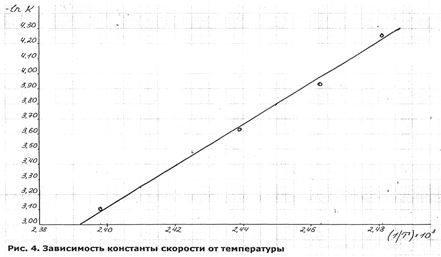
Из уравнения (3) следует, что график в координатах ![]() будет прямой линией:
будет прямой линией:

Уравнение (2) часто записывают в виде ![]() . Для характеристики скорости реакции часто пользуются величиной, называемой временем полупревращения (периодом полураспада), обозначаемой
. Для характеристики скорости реакции часто пользуются величиной, называемой временем полупревращения (периодом полураспада), обозначаемой ![]() - это время, в течение которого испытывает превращение половина взятого исходного вещества. Найдем выражение для
- это время, в течение которого испытывает превращение половина взятого исходного вещества. Найдем выражение для ![]() .
.
В выражение (2) подставляем ![]() :
: 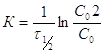 ,
, ![]()
Для реакции 1-го порядка время полупревращения не зависит от начальной концентрации.
Часто в кинетические уравнения подобного вида вводят величину Х, которая характеризует количество вещества, вступившего в реакцию, тогда ![]() и
и ![]() .
.
![]() ;
; 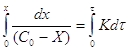
![]()
![]()
Все превращения радиоактивных веществ протекают по первому порядку. Уравнениями первого порядка описываются некоторые другие физические процессы, например, самопроизвольное излучение электронов невозбужденных атомов и молекул. По первому порядку протекает реакция ацетона:
![]()
Необратимые реакции второго порядка
![]()
![]() ;
; ![]() ;
;![]() ;
;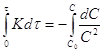 ;
;![]() (1)
(1)
![]() (2)
(2) ![]() (3)
(3)
Из (3) следует, что в координатах ![]() график будет прямой линией.
график будет прямой линией.
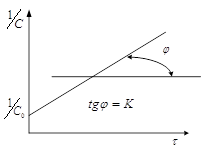
![]()
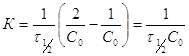
![]() ,
,
т.е. время полупревращения для реакции 2-го порядка обратно пропорционально начальной концентрации.
Рассмотрим более сложный случай: ![]()
Пусть Х – количество вещества А, вступившего в реакцию ко времени τ.
![]()
![]()
![]()
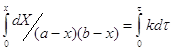
![]()
![]()
Реакциями 2-го порядка являются, например, реакции образования и разложения HI.
![]() ;
;
Омыление этилацетата щелочью и т.д.
Необратимые реакции третьего порядка
Такие реакции встречаются. В газовой фазе изучены пять таких реакций: взаимодействие оксида азота (II) с водородом, кислородом, хлором, бромом, йодом. Например: ![]() . В растворах известно большее количество таких реакций – окислительно-восстановительного характера. Рассмотрим простой случай, для которого
. В растворах известно большее количество таких реакций – окислительно-восстановительного характера. Рассмотрим простой случай, для которого ![]() и
и ![]() , где С – концентрация исходного вещества.
, где С – концентрация исходного вещества.
![]() ;
;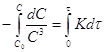 ;
;![]() (1)
(1) 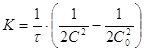 (2)
(2)
Следовательно, константа скорости реакции третьего порядка имеет размерность ![]() . В зависимости от способа выражения концентрации выражение (1) можно переписать в виде:
. В зависимости от способа выражения концентрации выражение (1) можно переписать в виде: ![]() , следовательно, в координатах
, следовательно, в координатах ![]() мы будем иметь прямую линию:
мы будем иметь прямую линию:
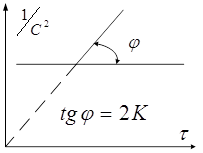
Это используют для графического определения константы скорости.
Выражение дл времени полупревращения найдем подстановкой в уравнение (2) ![]() :
: ![]() , т.е. время полупревращения обратно пропорционально квадрату начальной скорости.
, т.е. время полупревращения обратно пропорционально квадрату начальной скорости.
Р-ии дробного, нулевого
Для необратимой р-ии n–ого порядка для которой W=KCn. Для р-ии 2-го и 3-го порядка можно записать: ![]() (1).
(1).
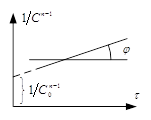
Выражения для времени полупревращения записывается ![]() (2). Уравнение 1 можно записать в виде
(2). Уравнение 1 можно записать в виде ![]() =>
=> ![]()
![]() . Дробный порядок р-ии указывает обычно на одновременное протекание нескольких этапов р-ии мало отличающихся друг от друга по скоростям ил на протекание обратимой р-ии. Часто дробный порядок имеют р-ии с участием атомов: CO+Cl2→COCl2.
. Дробный порядок р-ии указывает обычно на одновременное протекание нескольких этапов р-ии мало отличающихся друг от друга по скоростям ил на протекание обратимой р-ии. Часто дробный порядок имеют р-ии с участием атомов: CO+Cl2→COCl2. ![]()
![]() Нулевой порядок р-ии имеет место при постоянной скорости р-ии, что возможно при поддержании постоянной концентрации исходных веществ. Нулевой порядок встречается среди гетерогенных р-ий. Если х - количество вещества вступившего в р-ию, то
Нулевой порядок р-ии имеет место при постоянной скорости р-ии, что возможно при поддержании постоянной концентрации исходных веществ. Нулевой порядок встречается среди гетерогенных р-ий. Если х - количество вещества вступившего в р-ию, то ![]() ,
, ![]() ,
, 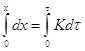 ,
, ![]()
![]() .
.
Методы определения порядка хим р-ии
Методы делятся на дифференциальные и интегральные. Дифференциальные используют исходное диф. ур ![]() . Интегральные методы используют уравнения после интегрирования. Среди интегральных методов используются: 1) подстановки 2) графический 3) определение по времени полупревращения. 1) получение опытным путём данных по зависимости концентрации реагир. вещества от времени подстановки в ур. для константы скорости р-ии различного порядка. Порядок р-ии определяется уравнением-подстановкой, в которое экспериментальных данных даёт постоянное значение константы скорости р-ии 2) экспериментальные данные представляются в виде графиков. Если в координатах
. Интегральные методы используют уравнения после интегрирования. Среди интегральных методов используются: 1) подстановки 2) графический 3) определение по времени полупревращения. 1) получение опытным путём данных по зависимости концентрации реагир. вещества от времени подстановки в ур. для константы скорости р-ии различного порядка. Порядок р-ии определяется уравнением-подстановкой, в которое экспериментальных данных даёт постоянное значение константы скорости р-ии 2) экспериментальные данные представляются в виде графиков. Если в координатах ![]() получится прямая линия, то р-ия 1-го порядка. Р-ия будет иметь 2-ой порядок если прямая линия получится в координатах
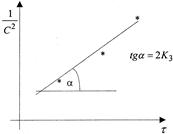
получится прямая линия, то р-ия 1-го порядка. Р-ия будет иметь 2-ой порядок если прямая линия получится в координатах ![]() . Для р-ии 3-го порядка линия зависимости наблюдается в координатах
. Для р-ии 3-го порядка линия зависимости наблюдается в координатах ![]() . 3) р-ию проводят 2 раза с разложением начальных концентр. Каждый раз определяют время полупревращения. Если окажется, что время полупревращения не зависит от начальных концентраций, значит р-ия первого порядка, т.к.
. 3) р-ию проводят 2 раза с разложением начальных концентр. Каждый раз определяют время полупревращения. Если окажется, что время полупревращения не зависит от начальных концентраций, значит р-ия первого порядка, т.к. ![]() . Если во втором опыте начальная концентрация была увеличена в 2 раза, а время полупревращения уменьшилось в 2 раза, значит р-ия 2-го порядка, т.к.
. Если во втором опыте начальная концентрация была увеличена в 2 раза, а время полупревращения уменьшилось в 2 раза, значит р-ия 2-го порядка, т.к. ![]() . Для р-ии 3-го порядка при том же самом условии время полупревращения уменьшится в 4 раза, т.к.
. Для р-ии 3-го порядка при том же самом условии время полупревращения уменьшится в 4 раза, т.к. ![]() . В общем случае если порядок
. В общем случае если порядок ![]() ,
, ![]() .
.
Если начальные концентрации ![]() , то
, то ![]() , если
, если ![]() , то
, то ![]() . Поделив, получим
. Поделив, получим ![]() . Логарифмируя, получим
. Логарифмируя, получим ![]() ,
, ![]() . Это соотношение сохранится и в случае определения времени превращения любой доли концентрации
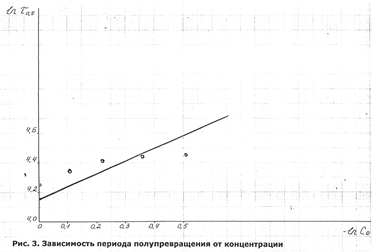
. Это соотношение сохранится и в случае определения времени превращения любой доли концентрации ![]() . Прежде рассмотрим диф. метод Вант-Гоффа. В основе метода лежит Ур
. Прежде рассмотрим диф. метод Вант-Гоффа. В основе метода лежит Ур ![]() . пусть измеряемое
. пусть измеряемое![]() ,
, ![]() ,
, ![]() - текущая концентрация исходного вещества в момент времени 1 и 2.
- текущая концентрация исходного вещества в момент времени 1 и 2. ![]() . После логарифмирования
. После логарифмирования ![]() ,
, ![]() (1). Скорость р-ии при концентрации
(1). Скорость р-ии при концентрации ![]() и
и ![]() определяется из зависимости
определяется из зависимости![]() .
. ![]() ,
, ![]() Часто получают не всю кривую
Часто получают не всю кривую ![]() , а производную определённой скорости при 2 концентрациях. Принимая, что
, а производную определённой скорости при 2 концентрациях. Принимая, что ![]() ,тогда
,тогда ![]() .
. ![]() Для определения ΔС измеряем концентрации вещества в какой-то момент времени и через небольшой промежуток Δτ. Графический вариант метода Вант-Гофа W=KCn прологарифмируем
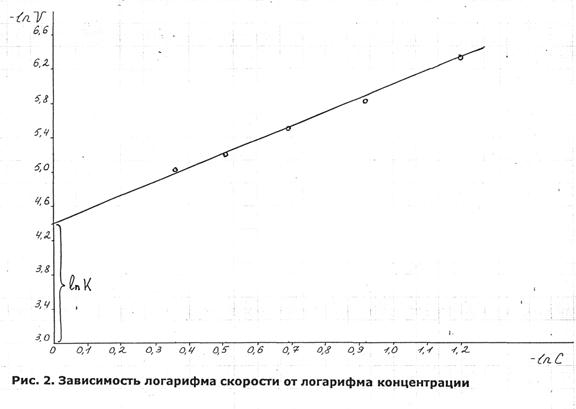
Для определения ΔС измеряем концентрации вещества в какой-то момент времени и через небольшой промежуток Δτ. Графический вариант метода Вант-Гофа W=KCn прологарифмируем ![]() => является линейной функцией lgC. Определяя скорость при нескольких концентрациях, строят график lgW-lgC tgα=n. Скорость р-ии W в различный момент времени определяется как и в предыдущем случае, но тангенс угла наклона касательной к положительному направлению оси абсцисс. Определяемый таким образом порядок р-ии называется временным порядком, он учитывает влияние на порядок продолжительности р-ии. Если использовать несколько кинетических кривых, то получим истинный порядок р-ии. Время и концентрация порядка могут не совпадать. Метод изоляции. Получим выражение для константы скорости р-ии различных порядков и рассмотрим методы определения порядка р-ии применимые для тех случаев, когда кинетическое уравнение имеет вид
=> является линейной функцией lgC. Определяя скорость при нескольких концентрациях, строят график lgW-lgC tgα=n. Скорость р-ии W в различный момент времени определяется как и в предыдущем случае, но тангенс угла наклона касательной к положительному направлению оси абсцисс. Определяемый таким образом порядок р-ии называется временным порядком, он учитывает влияние на порядок продолжительности р-ии. Если использовать несколько кинетических кривых, то получим истинный порядок р-ии. Время и концентрация порядка могут не совпадать. Метод изоляции. Получим выражение для константы скорости р-ии различных порядков и рассмотрим методы определения порядка р-ии применимые для тех случаев, когда кинетическое уравнение имеет вид ![]() . Пусть скорость хим. р-ии в зависимости от концентрации реагирующих веществ выражается Ур
. Пусть скорость хим. р-ии в зависимости от концентрации реагирующих веществ выражается Ур ![]() . n1, n2,.. – частные порядки р-ии или порядки р-ии соответствующие по 1-ому, 2-ому и 3-ему веществу. Сумма частных порядков определяет общий порядок р-ии. Чтобы определение частных порядков, а следовательно и общий поступают следующим образом: одно из веществ например 1-ое берут в нормальной концентрации, тогда как все остальные берут в большом избытке. Тогда концентрация этих веществ можно считать постоянными и зависимость скорости р-ии от концентрации выражается Ур
. n1, n2,.. – частные порядки р-ии или порядки р-ии соответствующие по 1-ому, 2-ому и 3-ему веществу. Сумма частных порядков определяет общий порядок р-ии. Чтобы определение частных порядков, а следовательно и общий поступают следующим образом: одно из веществ например 1-ое берут в нормальной концентрации, тогда как все остальные берут в большом избытке. Тогда концентрация этих веществ можно считать постоянными и зависимость скорости р-ии от концентрации выражается Ур ![]() . Одним из рассмотренных методов определён порядок р-ии по 1-ому веществу n1. Затем р-ию проводят снова, но в избытке берут все вещества, кроме 2-го и т.д.
. Одним из рассмотренных методов определён порядок р-ии по 1-ому веществу n1. Затем р-ию проводят снова, но в избытке берут все вещества, кроме 2-го и т.д.
Похожие работы
... исходных веществ и образования продукта реакции. В общем виде выражение (5) запишется формулой: (6) где vi - стехиометрические коэффициенты в уравнении реакции. Таким образом, скорость реакции равна скорости расходования (образования) данного вещества реакции, деленной на его стехиометрический коэффициент с учетом принятых знаков. Она всегда положительна. Скорость расходования исходных ...
... для следующего механизма реакции НX + hv→Н· + X Н· + НХ→Н2 + Х Х + Х→Х2. Ответ: А.0,45·10-7 Эйнштейн·с-1 . Б. γ=1,95. В. γ = 2 Глава 3. Кинетика гетерогенных реакций 3.1 Примеры 3.1.1. Образец сплава металла А и В длиной 0,5 см и образец металла В длиной 0,5 см спаяны друг с другом. Определите время, за которое в результате диффузии А ...
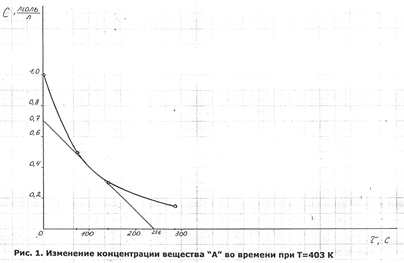
... скорости реакции Ki для различных температур и порядок реакции "n". Для случая, когда С0 (A) = C0 (B) кинетическое уравнение в дифференциальной форме имеет вид: V = - dc / dτ = K * Cn, (6) где V - скорость химической реакции; K - константа скорости; С - текущая концентрация. Интегрирование этого уравнения дает выражение: Kτ = (1/n-1) (1/Сn-1-1/С0n-1) (7) Зная порядок ...
... а також температури на швидкість ацидолізу епіхлоргідрину. Для вирішення цих питань було проведено цілеспрямоване варіювання структури карбонової кислоти, структури та концентрації каталізатора, а також варіювання температури в досліджуваній реакції (1). Реакції ацидолізу епіхлоргідрину оцтовою кислотою та її похідними виконано в інтервалі температур 300 - 600С при концентрації каталізатору від ...

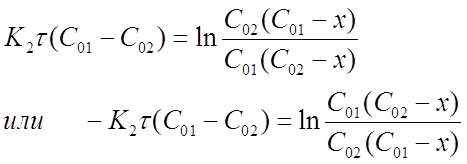


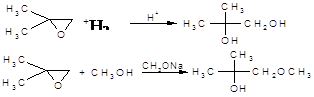
0 комментариев