За даними 25 підприємств за допомогою аналітичного групування з рівновеликими інтервалами (в три групи) прослідкувати залежність між виробництвом продукції та собівартістю зернових.
1. Результати групування оформити в таблиці та детально проаналізувати.
2. Оцінити суттєвість різниці середніх значень собівартості продукції по підприємствах першої та третьої груп за допомогою t-критерія Стьюдента.
| Підприємства | Вироблено продукції, тис. шт. | Загальна сума витрат, тис. грн. | Собівартість одиниці продукції, грн. |
| 1 | 8,5 | 35 | 9,15 |
| 2 | 2,7 | 29 | 7,01 |
| 3 | 4,0 | 67 | 8,37 |
| 4 | 9,8 | 59 | 9,64 |
| 5 | 2,5 | 31 | 9,11 |
| 6 | 4,9 | 68 | 9,09 |
| 7 | 7,1 | 23 | 7,95 |
| 8 | 11,0 | 91 | 7,61 |
| 9 | 5,2 | 43 | 8,20 |
| 10 | 6,9 | 37 | 8,77 |
| 11 | 10,7 | 53 | 9,00 |
| 12 | 4,1 | 20 | 9,35 |
| 13 | 7,3 | 61 | 9,41 |
| 14 | 9,7 | 46 | 8,79 |
| 15 | 6,3 | 32 | 8,95 |
| 16 | 5,2 | 29 | 8,99 |
| 17 | 9,0 | 37 | 9,95 |
| 18 | 8,9 | 59 | 8,11 |
| 19 | 7,1 | 43 | 8,40 |
| 20 | 6,4 | 27 | 7,50 |
| 21 | 10,1 | 85 | 8,33 |
| 22 | 3,9 | 70 | 7,99 |
| 23 | 4,5 | 31 | 9,13 |
| 24 | 6,3 | 55 | 8,45 |
| 25 | 9,7 | 42 | 9,39 |
Рішення:
Проведемо угруповання за кількістю виготовленої продукції.
Для проведення групування визначимо інтервал групування:
![]() ,
,
де ![]() ,
,![]() - відповідно найбільше і найменше значення групувальної ознаки;
- відповідно найбільше і найменше значення групувальної ознаки;
![]() - кількість груп;
- кількість груп;
![]() інтервал.
інтервал.
Отже інтервал групування дорівнює:
і = (11 – 2,5)/3 = 2,84
Відобразимо дані групування в таблицю:
| № п/п | Вироблено продукції, тис. шт. | Загальна сума витрат, тис. грн. | Собівартість одиниці продукції, грн. | Кількість підприємств |
| 1 | 2,5 – 5,34 | 338 | 77,24 | 9 |
| 2 | 5,34 – 8,18 | 278 | 59,43 | 7 |
| 3 | 8,18 – 11,02 | 507 | 79,97 | 9 |
Для визначення тісноти зв’язку між кількістю виготовленої продукції і собівартістю продукції розрахуємо коефіцієнт кореляції:
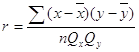
Для розрахунку потрібно визначити середнє квадратичне відхилення обох ознак, використовуючи формулу:
![]()
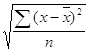
![]() =171/25 = 6,872
=171/25 = 6,872
![]() = 216,64/25 = 8,67
= 216,64/25 = 8,67
Дані розраховані за допомогою формули середньої звичайної:
![]()
Розрахуємо середнє квадратичне відхилення:
![]()
![]() = 2,49
= 2,49
![]() =
= ![]() = 0,49
= 0,49
![]() 8,3179/30,5 = 0,27
8,3179/30,5 = 0,27
як показали розрахунки між кількістю виготовленої продукції і собівартістю одиниці продукції існує тісний зв’язок.
Проведемо оцінку суттєвості різниці середніх значень собівартості продукції по підприємствах першої та третьої груп за допомогою t-критерія Стьюдента. В таблиці наведено дані першої групи:
| № п/п | Вироблено продукції, тис. шт. | Собівартість одиниці продукції, грн. |
| 1 | 2,5 | 9,11 |
| 2 | 2,7 | 7,01 |
| 3 | 3,9 | 7,99 |
| 4 | 4 | 8,37 |
| 5 | 4,1 | 9,35 |
| 6 | 4,5 | 9,13 |
| 7 | 4,9 | 9,09 |
| 8 | 5,2 | 8,2 |
| 9 | 5,2 | 8,99 |
Шляхом розрахунку середньої арифметичної звичайної середнє значення собівартості одиниці продукції дорівнює 8,58 грн. Дисперсія дорівнює 0,51, середнє квадратичне відхилення 0,72.
Знайдемо коефіцієнт варіації:
![]()
U = (0,72/8,58) * 100 = 8,39 %
t-критерій Стьюдента в даному випадку, для ступенів волі f = 9 – 1 = 8, і рівня довірчої імовірності 95 %, дорівнює 2,3060 таким чином довірчий інтервал для середнього значення дорівнює від 8,15 до 9,0.
Третя група має вигляд:
| № п/п | Вироблено продукції, тис. шт. | Собівартість одиниці продукції, грн. |
| 1 | 8,5 | 9,15 |
| 2 | 8,9 | 8,11 |
| 3 | 9 | 9,95 |
| 4 | 9,7 | 8,79 |
| 5 | 9,7 | 9,39 |
| 6 | 9,8 | 9,64 |
| 7 | 10,1 | 8,33 |
| 8 | 10,7 | 9 |
| 9 | 11 | 7,61 |
Аналогічним чином знайдемо:
![]() =79,97/9 = 8,89
=79,97/9 = 8,89
G2 = 4,5862/9 = 0,51
G = 0,71
U = (0,71/8,89) * 100 = 7,99
t-критерій Стьюдента в даному випадку, для ступенів волі f = 9 – 1 = 8, і рівня довірчої імовірності 95 %, дорівнює 2,36, таким чином довірчий інтервал для середнього значення дорівнює від 8,45 до 9,3.
Задача 2
За даними 25 підприємств побудувати ряд розподілу в 5 інтервалів (n = ![]() ) за загальною сумою витрат.
) за загальною сумою витрат.
За рядом розподілу обчислити:
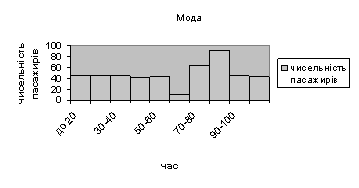
1. Моду
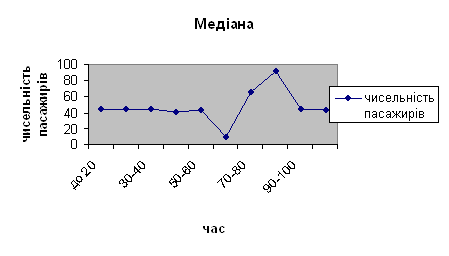
2. Медіану
3. Зобразити графічно ряди розподілу: побудувати полігон та гістограму розподілу, огіву, кумуляту інтервального ряду розподілу.
| Підприємства | Вироблено продукції, тис. шт. | Загальна сума витрат, тис. грн. | Собівартість одиниці продукції, грн. |
| 1 | 8,5 | 35 | 9,15 |
| 2 | 2,7 | 29 | 7,01 |
| 3 | 4,0 | 67 | 8,37 |
| 4 | 9,8 | 59 | 9,64 |
| 5 | 2,5 | 31 | 9,11 |
| 6 | 4,9 | 68 | 9,09 |
| 7 | 7,1 | 23 | 7,95 |
| 8 | 11,0 | 91 | 7,61 |
| 9 | 5,2 | 43 | 8,20 |
| 10 | 6,9 | 37 | 8,77 |
| 11 | 10,7 | 53 | 9,00 |
| 12 | 4,1 | 20 | 9,35 |
| 13 | 7,3 | 61 | 9,41 |
| 14 | 9,7 | 46 | 8,79 |
| 15 | 6,3 | 32 | 8,95 |
| 16 | 5,2 | 29 | 8,99 |
| 17 | 9,0 | 37 | 9,95 |
| 18 | 8,9 | 59 | 8,11 |
| 19 | 7,1 | 43 | 8,40 |
| 20 | 6,4 | 27 | 7,50 |
| 21 | 10,1 | 85 | 8,33 |
| 22 | 3,9 | 70 | 7,99 |
| 23 | 4,5 | 31 | 9,13 |
| 24 | 6,3 | 55 | 8,45 |
| 25 | 9,7 | 42 | 9,39 |
Рішення:
Для проведення групування визначимо інтервал групування за допомогою наступної формули:
![]() ,
,
де ![]() ,
,![]() - відповідно найбільше і найменше значення групувальної ознаки;
- відповідно найбільше і найменше значення групувальної ознаки;
![]() - кількість груп;
- кількість груп;
![]() інтервал.
інтервал.
Отже інтервал групування дорівнює:
і = (91 – 20)/5 = 14,2
| № п/п | Продуктивність праці | Кількість заводів |
| 1 | 20 – 34,2 | 8 |
| 2 | 34,2 – 48,4 | 7 |
| 3 | 48,4 – 62,6 | 5 |
| 4 | 62,6 – 76,8 | 3 |
| 5 | 76,8 - 91 | 2 |
Мода – це варіант, що частіше за все зустрічається в статистичному ряді. Мода розраховується за допомогою наступної формули:
Мо = х0 + і (fm – fm-1)/((fm – fm-1)(fm – fm+1))
де х0 – нижня границя модального інтервалу;
і – величина інтервалу;
fm – частота модального інтервалу;
fm-1 – частота інтервалу, що передує модальному інтервалу;
fm+1 – частота наступного інтервалу за модальним інтервалом.
Проведемо відповідні розрахунки:
Мо = 20 + 14,2![]() =20 + 14,2 * 0,067 = 20,95
=20 + 14,2 * 0,067 = 20,95
Медіана розраховується за допомогою формули:
Ме = х0 + і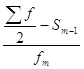
де (і Σf)/2 – сума всіх частот пополам;
Sm-1 – накопичена частота інтервалу, що передує медіанному;
fm – частота медіанного інтервалу.
Ме = 34,2 + 14,2 * ((12,5-8)/7) = 43,33
Побудуємо за даними групуваннями гістограму:
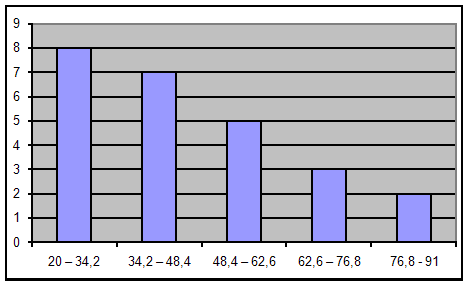
побудуємо полігон:
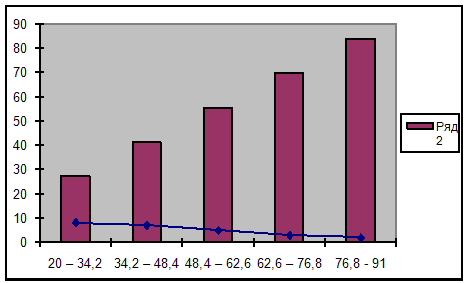
побудуємо кумулятивну криву:
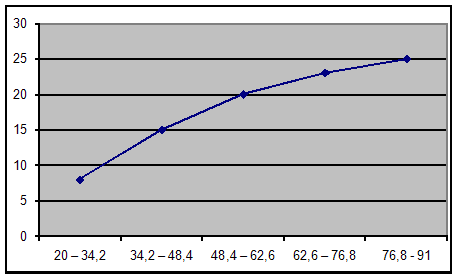
побудуємо огіву:
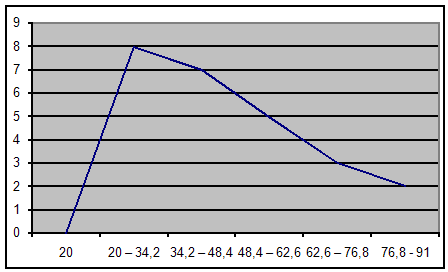
Задача 3
За даними 25 цехів заводів скласти і розв’язати рівняння кореляційної залежності виробництва литва на одного робітника і собівартістю 1 т, обчисливши при цьому ці показники для кожного заводу. Обчислити коефіцієнт кореляції. Побудувати графік кореляційної залежності. Зробити короткі висновки. Обчислення оформити в таблиці.
| № п/п заводів | Виробництво литва на одного працівника, т | Брак, % | Собівартість 1 т, грн. |
| 1 | 14,6 | 4,2 | 239 |
| 2 | 13,5 | 6,7 | 254 |
| 3 | 21,6 | 5,5 | 262 |
| 4 | 17,4 | 7,7 | 251 |
| 5 | 44,8 | 1,2 | 158 |
| 6 | 111,9 | 2,2 | 101 |
| 7 | 20,1 | 8,4 | 259 |
| 8 | 28,1 | 1,4 | 186 |
| 9 | 22,3 | 4,2 | 204 |
| 10 | 25,3 | 0,9 | 198 |
| 11 | 56,0 | 1,3 | 170 |
| 12 | 40,2 | 1,8 | 173 |
| 13 | 40,6 | 3,3 | 197 |
| 14 | 75,8 | 3,4 | 172 |
| 15 | 27,6 | 1,1 | 201 |
| 16 | 88,4 | 0,1 | 130 |
| 17 | 16,6 | 4,1 | 251 |
| 18 | 33,4 | 2,3 | 195 |
| 19 | 17,0 | 9,3 | 282 |
| 20 | 33,1 | 3,3 | 196 |
| 21 | 30,1 | 3,5 | 186 |
| 22 | 65,2 | 1,0 | 176 |
| 23 | 22,6 | 5,2 | 238 |
| 24 | 33,4 | 2,3 | 204 |
| 25 | 19,7 | 2,7 | 205 |
Рішення:
Для вияву і тісноти взаємозв’язку між показниками використаємо кореляційно - регресійні методи аналізу. Основною ціллю нашого аналізу є отримання апроксимуючої функції:
![]()
що найбільш реально відображає зв’язок між показниками, що вивчаються.
Для побудови одно факторної моделі розглянемо:
![]()
або
![]()
![]()
Параметри розраховуються по методу найменших квадратів, тобто коли система нормативних рівнянь при вирівнюванні має вигляд:
![]()
![]()
![]()
![]()
звідси
![]()
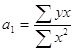
Розрахункові дані наведені в таблиці:
| № п/п заводів | Виробництво литва на одного працівника, т (х) | Собівартість 1 т, грн. (у) | ху | х2 |
| 1 | 14,6 | 239 | 3489,4 | 57121 |
| 2 | 13,5 | 254 | 3429 | 64516 |
| 3 | 21,6 | 262 | 5659,2 | 68644 |
| 4 | 17,4 | 251 | 4367,4 | 63001 |
| 5 | 44,8 | 158 | 7078,4 | 24964 |
| 6 | 111,9 | 101 | 11301,9 | 10201 |
| 7 | 20,1 | 259 | 5205,9 | 67081 |
| 8 | 28,1 | 186 | 5226,6 | 34596 |
| 9 | 22,3 | 204 | 4549,2 | 41616 |
| 10 | 25,3 | 198 | 5009,4 | 39204 |
| 11 | 56,0 | 170 | 9520 | 28900 |
| 12 | 40,2 | 173 | 6954,6 | 29929 |
| 13 | 40,6 | 197 | 7998,2 | 38809 |
| 14 | 75,8 | 172 | 13037,6 | 29584 |
| 15 | 27,6 | 201 | 5547,6 | 40401 |
| 16 | 88,4 | 130 | 11492 | 16900 |
| 17 | 16,6 | 251 | 4166,6 | 63001 |
| 18 | 33,4 | 195 | 6513 | 38025 |
| 19 | 17,0 | 282 | 4794 | 79524 |
| 20 | 33,1 | 196 | 6487,6 | 38416 |
| 21 | 30,1 | 186 | 5598,6 | 34596 |
| 22 | 65,2 | 176 | 11475,2 | 30976 |
| 23 | 22,6 | 238 | 5378,8 | 56644 |
| 24 | 33,4 | 204 | 6813,6 | 41616 |
| 25 | 19,7 | 205 | 4038,5 | 42025 |
| Всього | 919,3 | 5088 | 165132,3 | 1080290 |
![]() 919,3/25 = 36,772
919,3/25 = 36,772
![]() 1651323/1080290 = 0,153
1651323/1080290 = 0,153
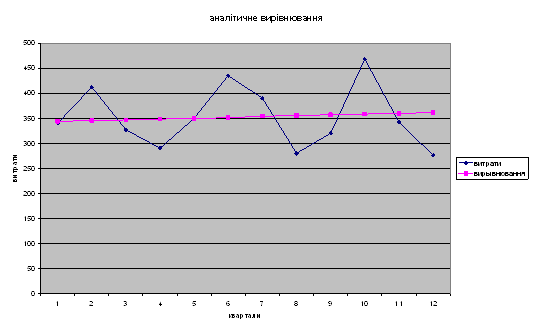
таким чином рівняння кореляційної залежності має вигляд:
![]() = 36,772 + 0,153 х
= 36,772 + 0,153 х
знайдемо коефіцієнт кореляції:
для цього визначимо середнє квадратне відхилення показників х і y:
![]()
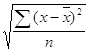
Розрахуємо середні показники виробництва литва на одного працівника і собівартості однієї тони продукції:
![]() =919,3/25 = 36,77
=919,3/25 = 36,77
![]() = 5088/25 = 203,52
= 5088/25 = 203,52
Розрахунки оформимо в таблиці:
№ п/п заводів |
|
|
|
|
|
| 1 | -22,17 | 35,48 | 491,5089 | 1258,8304 | -786,5916 |
| 2 | -23,27 | 50,48 | 541,4929 | 2548,2304 | -1174,6696 |
| 3 | -15,17 | 58,48 | 230,1289 | 3419,9104 | -887,1416 |
| 4 | -19,37 | 47,48 | 375,1969 | 2254,3504 | -919,6876 |
| 5 | 8,03 | -45,52 | 64,4809 | 2072,0704 | -365,5256 |
| 6 | 75,13 | -102,52 | 5644,5169 | 10510,3504 | -7702,3276 |
| 7 | -16,67 | 55,48 | 277,8889 | 3078,0304 | -924,8516 |
| 8 | -8,67 | -17,52 | 75,1689 | 306,9504 | 151,8984 |
| 9 | -14,47 | 0,48 | 209,3809 | 0,2304 | -6,9456 |
| 10 | -11,47 | -5,52 | 131,5609 | 30,4704 | 63,3144 |
| 11 | 19,23 | -33,52 | 369,7929 | 1123,5904 | -644,5896 |
| 12 | 3,43 | -30,52 | 11,7649 | 931,4704 | -104,6836 |
| 13 | 3,83 | -6,52 | 14,6689 | 42,5104 | -24,9716 |
| 14 | 39,03 | -31,52 | 1523,3409 | 993,5104 | -1230,2256 |
| 15 | -9,17 | -2,52 | 84,0889 | 6,3504 | 23,1084 |
| 16 | 51,63 | -73,52 | 2665,6569 | 5405,1904 | -3795,8376 |
| 17 | -20,17 | 47,48 | 406,8289 | 2254,3504 | -957,6716 |
| 18 | -3,37 | -8,52 | 11,3569 | 72,5904 | 28,7124 |
| 19 | -19,77 | 78,48 | 390,8529 | 6159,1104 | -1551,5496 |
| 20 | -3,67 | -7,52 | 13,4689 | 56,5504 | 27,5984 |
| 21 | -6,67 | -17,52 | 44,4889 | 306,9504 | 116,8584 |
| 22 | 28,43 | -27,52 | 808,2649 | 757,3504 | -782,3936 |
| 23 | -14,17 | 34,48 | 200,7889 | 1188,8704 | -488,5816 |
| 24 | -3,37 | 0,48 | 11,3569 | 0,2304 | -1,6176 |
| 25 | -17,07 | 1,48 | 291,3849 | 2,1904 | -25,2636 |
| Всього | 14889,4305 | 44780,24 | -21963,636 |
![]()
![]() = 24,4
= 24,4
![]() =
= ![]() = 42,32
= 42,32
Для розрахунку коефіцієнта кореляції використовується формула:
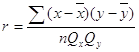
r = (-21963,636)/25815,2 = - 0,85
Оскільки коефіцієнт кореляції дорівнює показнику меншому за 0,3, то це свідчить про слабкий кореляційний зв’язок між параметрами, що аналізуються.
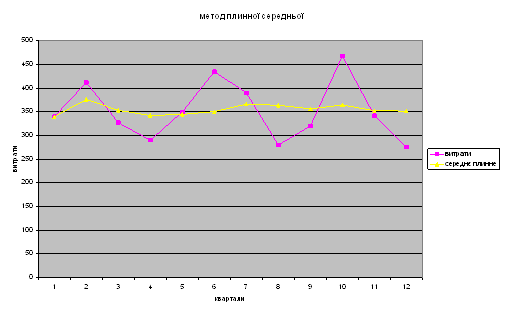
Побудуємо графік кореляційної залежності:
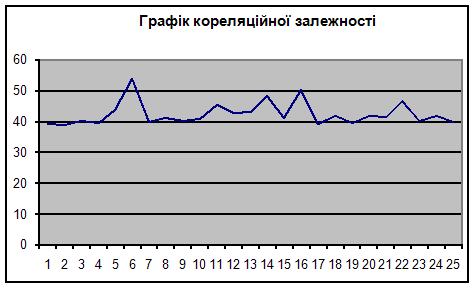
Задача 4
Товарооборот продовольчого магазину по основних групах товарів становив:
| Назва продукту | Товарооборот у поточних цінах, тис. грн. | Зміни кількості продукції у звітному періоді порівняно з базисним, % | |
| базисний | звітний | ||
| М’ясо | 35 | 50 | +12 |
| Молоко | 46 | 46 | +7 |
| Овочі | 35 | 55 | -10 |
Обчислити:
1. Обчислити загальні індекси та абсолютні прирости фізичного обсягу реалізації, цін, товарообороту.
2. Показники взаємозв’язку між ними.
3. Зробити короткі висновки.
Рішення:
Товарооберт, це рух товарної маси від виробника до споживача шляхом купівлі – продажу, шляхом обміну товару на гроші.
Взаємозв’язок між ціною (р) і кількістю проданих товарів (q) можна виразити через об’єм товарооберту, що дорівнює:
![]()
у випадку коли за період, що розглядається товар продавався і покупався кілька разів, то вартість цього товару стільки ж раз буде враховуватись в об’ємі товарообету.
Динаміка товарооберту вивчається в поточних цінах і спів ставних, загальний індекс товар оберту розраховується за допомогою формули:
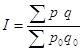
де I – загальний індекс товароберту;
p0p – ціни в базисному і звітному періоді відповідно;
q0q– об’єм виготовленої продукції у базисному і звітному періоді.
І = 151/116 = 1,3 або 130 %Абсолютний приріст = 151 – 116 = 35 тис.грн..
Таким чином товарооберт у звітному періоді збільшився на 35 тис. грн.. в порівнянні з базисним.
Виходячи з даних наведених у таблиці кількість м’ясної продукції в звітному періоді відносно базисного зросла на 12 %, отже індекс фізичного об’єму м’ясної продукції склав 1,12 або 112 %, при цьому виходячи з залежності, індекс цін дорівнює 0,013, або 1,3 %. Аналогічно індекс фізичного об’єму молочних продуктів склав 107 %, при цьому індекс ціни 0,0093, або 0,93 %. Обсяг продажу овочів знизився на 10 %, отже індекс фізичного об’єму продажу овочів склав 90 % або 0,9, при цьому індекс ціни на овочі склав 0,018 або 1,8 %.
Задача 5
Є дані про динаміку валового виробництва продукції, тис. т.
| Роки | Валовий збір, тис. т | Базисні показники динаміки | |||
| Абсолютний приріст, тис. т | Темп зростання, % | Темп приросту, % | Абсолютне значення 1 % приросту, тис. т | ||
| 1997 | 132,8 | ||||
| 1998 | 134,85 | 2,85 | 2,05 | 1,05 | 2,71 |
| 1999 | 929,6 | 796,8 | 7,0 | 6,0 | 132,8 |
| 2000 | 9827,2 | 9694,4 | 74,0 | 73,0 | 132,8 |
| 2001 | 796,8 | 664 | 6 | 5,0 | 132,8 |
| 2002 | 13678,4 | 13545,6 | 103,0 | 102,0 | 132,8 |
| 2003 | 398,4 | 265,6 | 3,0 | 2,0 | 132,8 |
Використовуючи взаємозв’язок показників динаміки, визначити рівні та показники, що відсутні в таблиці.
Рішення:
Оскільки абсолютний приріст валового виробництва продукції визначається, як відношення між двома рівнями ряду:
![]() ,
,
то знайдемо показник валового збору продукції в 1998 році:
![]()
![]() = 2,85 + 132 = 134,85
= 2,85 + 132 = 134,85
у відповідності до формули знайдемо темп зростання:
![]()
Т1998 = 134,85/132,8 = 2,05
Темп приросту знаходиться за формулою:
ΔТ = ![]() Тб – 1
Тб – 1
ΔТ1998 = 2,05 – 1 = 1,05
Абсолютне значення приросту розраховується за допомогою наступної формули:
λ = Δ/ΔТ
λ = 2,85/1,05 = 2,71
тобто 2,71 є абсолютною величиною одного проценту приросту валового збору виробництва.
Шляхом математичних розрахунків, через вказані формули і підстановки відомих показників з таблиці, розрахуємо і занесемо до таблиці невідомі елементи, використовуючи базисний метод розрахунків.
Похожие работы
... стерство освіти і науки України; 2. Міністерство охорони здоров’я України; 3. Державний комітет України із земельних ресурсів; 4. Державний комітет України із природних ресурсів; 5. Моторин Р. М. Економічна статистика.-К.:КНЕУ,2005; 6. Статистика:підручник/ С.С Герасименко, А.В.Головач, А.М. Єріна та ін.:За наук. ред. д-ра. екон. наук С.С Герасименка – ге вид. перероб. і доп.:-К.КНЕУ,2000. ...
... цінностей з країни, за які в подальшому її резиденти отримують виплати в іноземній валюті. Дебет платіжного балансу – це надходження вартостей у країну, за які її резиденти повинні витрачати іноземну валюту. Статистика валютних курсів Валютний курс як інструмент міжнародних угод характеризує економічні системи, між якими відбувається рух товарів, послуг та капіталів. Під валютним курсом ...
... . Практикум. За ред. Єріної А.М., Пальянс З.А. – синій колір, стислий виклад теорії, приклад рішень, задачі. Рекомендується! 2. Ковтун Н.В., Столяров В,С. Загальна теорія статистики. Курс лекцій. К.: Хвиля, 1996. 3. Общая теория статистики. Учебник. Под общей редакцией проф. Елисеевой И.И. М.: Финансы и статистика, 1995. 4. Общая теория статистики. Учебник. Под редакцией Ефимовой М.Р. М.: 1996. 5. ...
... праці, тобто ефективність використання трудових ресурсів, фондовіддачу і фондомісткість продукції, окупність виробничих витрат, рівень рентабельності виробництва. Розділ 2. Економічна ефективність рослинницьких галузей 2.1 Виробничо-економічна характеристика радгоспу Степовий Миколаївського району Радгосп Степовий розташований у Миколаївському районі на півдні області на відстані 55 км. ...
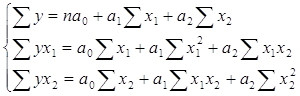
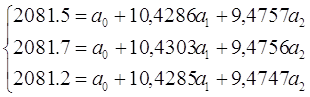
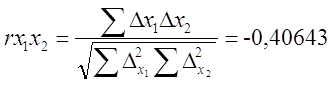
0 комментариев