Сегодня мы с вами отправимся в путешествие в один из уголков страны "Алгебра", в край "Многочлены". Выясним, знаете ли вы, что такое многочлены и умеете ли вы выполнять арифметические действия над многочленами.
Но нельзя идти в гости, не зная порядков и законов страны. Давайте проверим, как мы с вами готовы к такому путешествию. В этой стране много всяких диковинных названий. Давайте их вспомним.
Что такое многочлен?
Как можно по другому назвать многочлен?
Что такое многочлен с одной переменной?
Что такое однородный многочлен?
Как можно назвать одночлен? (моном)
Как можно назвать двучлен? (бином)
Как можно назвать трехчлен? (трином)
Каким правилом мы пользуемся чтобы умножить одночлен на многочлен?
Итак отправляемся в путешествие. В краю "Многочлены" мы познакомимся с математическими лабораториями и примем участие в их исследованиях. Но прежде необходимо пройти испытание, которое будет служить нам пропуском в эти лаборатории.
I. "Испытание" (устная работа)
1 Перед вами полином ![]()
Укажите мономы, из которых составлен этот полином.
2. Есть имена многочленов:
а) многочлен стандартного вида
б) многочлен нестандартно вида,
в) бином,
г) трехчлен,
д) полином с одной неизвестной,
е) полином третьей степени.
Какие имена отнесли бы вы к следующим многочленам?
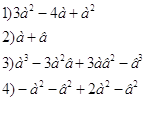
3) Вместо * поставьте такой одночлен чтобы получился многочлен не содержащий переменной
![]()
4). Вместо * поставьте такой одночлен чтобы получился многочлен 5-й степени
![]()
5). Выполните умножение
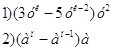
6). Вместо *какой нужно записать одночлен, чтобы выполнялось равенство
![]()
![]() II. "Лаборатория уравнений"
II. "Лаборатория уравнений"
Перед нами лаборатория уравнений. Давайте примем участие в исследованиях этой лаборатории. Вы должны провести 2 исследования:
1-е:
![]()
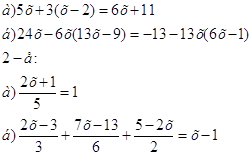
Проверим результаты исследований поменявшись тетрадями с помощью кодоскопа.
Какими приемами при решении уравнений мы пользовались?
III. "Лаборатория доказательств".
Два ученика решают на дополнительных досках. Остальные самостоятельно.
№676 (а), №677 (а)
Какие приемы применяли при доказательстве?
В свободное время от исследований можно выполнять тест.
IIII. "Лаборатория задач".
Решим у доски задачу из учебника.
Сформулируйте задачу для которой можно было бы использовать уравнение
![]()
Подведем итоги наших исследований. Посчитаем количество набранных баллов и выставим отметку за урок.
Итоги подводятся с помощью таблицы.
| Количество очков | оценка | уровень | Комментарии |
| 10 | Очень высокий | Так держать! | |
| 9 | Высокий | Чуть-чуть и | |
| 8 | Высокий | будет 10 | |
| 7 | Средний | Будьте внимательны на | |
| 6 | Средний | уроке | |
| 5 | низкий | И о чем только думаете на уроке? | |
| 4 | Низкий | ||
| 3 | Очень низкий | Без комментарий | |
| 2 | нулевой |
УРОК ПО ТЕМЕ
"Многочлены" (урок обобщение)
7 класс
Схема путешествия.
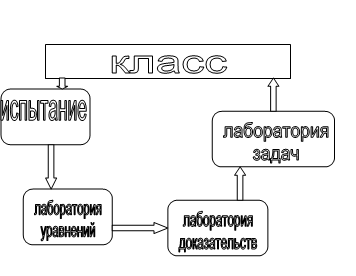
Похожие работы
... Для повернення до режиму меню слід натиснути довільну клавішу. 6.Для виходу з пакету в режимі меню ввести число 0. Висновки В даній роботі реалізована задача «Виконання символьних операцій з многочленами». Здійснено математичний опис задачі, постановку задачі та розробку програмного пакету згідно з постановкою. Роботу пакету перевірено на контрольному прикладі, одержано результати, що ...
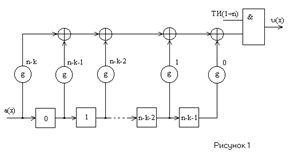
... , если его длина n=qm-1 над GF(q). Если длина кода меньше длины примитивного кода, то код называется укороченным или непримитивным. Общее свойство кодовых слов циклического кода - это их делимость без остатка на некоторый многочлен g(x), называемый порождающим. Результатом деления двучлена xn+1 на многочлен g(x) является проверочный многочлен h(x). При декодировании циклических кодов используются ...
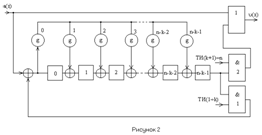
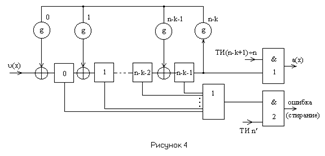
ирования циклического кода с обнаружением ошибок, по аналогии с процессом кодирования, использует два способа: - при кодировании "классическим" способом декодирование основано на использовании свойства делимости без остатка кодового многочлена (x) циклического (n,k)-кода на порождающий многочлен g(x). Поэтому алгоритм декодирования включает в себя деление принятого кодового слова, описываемого ...
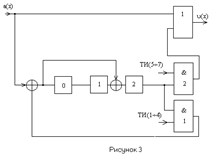
... , и в другом случае, схема же (7.k) преимущественно «комплексная» — действительным коэффициентам могут соответствовать комплексные параметры. Появление комплексных чисел при вычислении действительных многочленов намного увеличивает число арифметических операций5. К счастью, в 1960году схему (7.k) небольшим усложнением удалось превратить в действительную; однако полные доказательства в этом случае ...
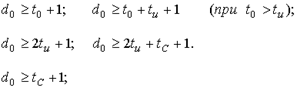
0 комментариев