Навигация
Математическая модель установки и преобразование ее в пространство состояний
44027
знаков
4
таблицы
15
изображений
2. Математическая модель установки и преобразование ее в пространство состояний
Математическая модель задана в виде матрицы передаточных функций.
| u1 | u2 | u3 | u4 | |
| y1 |
|
|
|
|
| y2 | - |
|
|
|
| y3 |
|
|
|
|
| y4 |
|
|
|
|
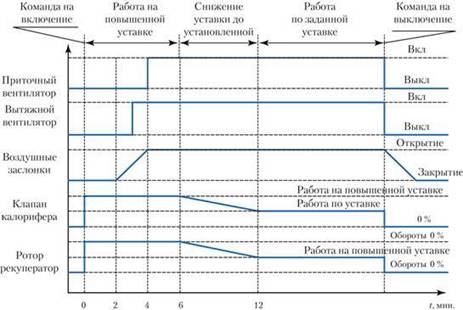
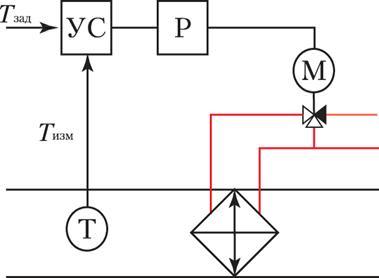
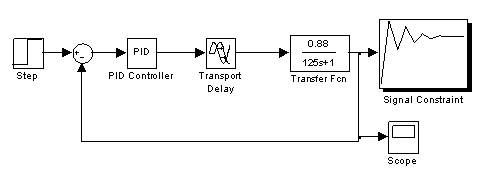
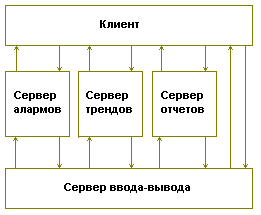
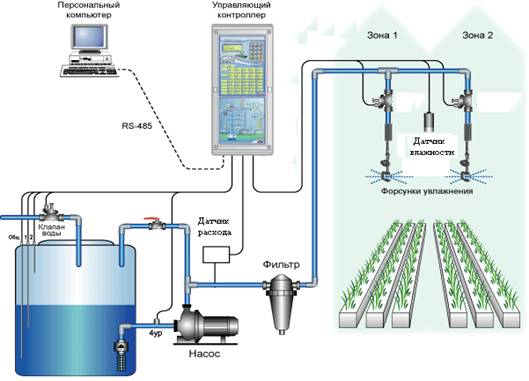
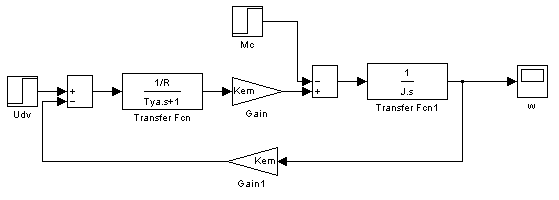
Блок-схема системы приведена в - Приложении 1.
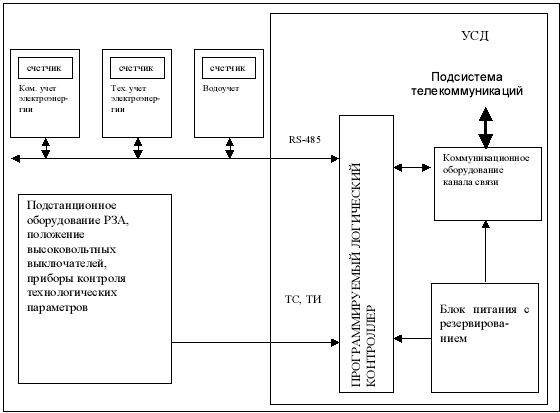
Развёрнутая схема системы с учётом запаздывания приведена в - Приложении 2.
В исходных данных, модель дана как мы видим в виде матриц передаточных функций. Для преобразования передаточных функций в пространство состояний использовалась функция матлаба tf2ss. Для проверки правильности преобразования следует найти собственные значения матрицы А с помощью функции еig и убедиться, что или все собственные значения матрицы А имеют отрицательные действительные части, или число нулевых собственных значений совпадает с числом интегральных звеньев в исходной модели. Окончательно система должна быть представлена матрицами A,B,C,D
Ниже приведены матрицы модели в пространстве состояний
где х- состояние систем;
y- измеряемые входы;
f- возмущение;
u- управление.
Матрицы системы имеют вид:
A=[-1/118 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
1/26.7 -1/26.7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 4/14 -2/14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 -1/1300 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 4/80 -2/80 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 -1/118 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 1/26.7 -1/26.7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 4/-14 -2/14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 -1/118 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 1/26.7 -1/26.7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 4/14 -2/14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 -1/430 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 4/80 -2/80 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 -1/470 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 4/170 -2/170 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/480 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4/180 -2/180 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/430 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4/100 -2/100 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/840 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4/100 -2/100 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/800 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4/250 -2/250 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/570 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4/300 -2/300 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/450 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4/150 -2/150 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/640 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4/220 -2/220 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/540 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4/300 -2/300 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/950 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4/480 -2/480];
Матрица входа:
B=[6.5/118000;
0000;
0000;
0-6.1/130000;
0000;
006.5/1180;
0000;
0000;
0 006.5/118;
0 000;
0 000;
00.4/43000;
0000;
000.3/4700;
0000;
0000.9/480;
0000;
-0.7/430000;
0000;
00.2/84000;
0000;
000.9/8000;
0000;
0000.5/570;
0000;
-0.1/450000;
0000;
00.1/64000;
0000;
000.1/5400;
0000;
0000.2/950;
0000];
Матрица измерений:
C=[0 -1 1 -1 1 0 -1 -1 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 -1 1 -1 1 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 1 -1 1 -1 1 -1 1 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 1 -1 1 -1 1 -1 1];
3. Преобразование математической модели в дискретное время и ее проверка с помощью построения разгонных характеристик
Для преобразования математической модели в дискретное время пользуется функция матлаба с2d. Шаг дискретизации может быть выбран с учетом того, что процессы в замкнутой системе будут где-то в 10 раз быстрее, чем в объекте. То есть:
dt=0.01/max(abs(eig(A)));
[Ad,Bd]=c2d(A,B,dt);
Проверить найденную модель в дискретном времени следует с помощью расчета разгонных характеристик. Для этого следует используем функцию dstep. Для вывода графиков используем функции: subplot, plot, grid.
Матрицы модели в дискретном времени:
Ad =
Columns 1 through 12
0.9941 0 0 0 0 0 0 0 0 0 0 0
0.0258 0.9741 0 0 0 0 0 0 0 0 0 0
0.0025 0.1878 0.9048 0 0 0 0 0 0 0 0 0
0 0 0 0.9995 0 0 0 0 0 0 0 0
0 0 0 0.0347 0.9827 0 0 0 0 0 0 0
0 0 0 0 0 0.9941 0 0 0 0 0 0
0 0 0 0 0 0.0258 0.9741 0 0 0 0 0
0 0 0 0 0 -0.0025 -0.1878 0.9048 0 0 0 0
0 0 0 0 0 0 0 0 0.9941 0 0 0
0 0 0 0 0 0 0 0 0.0258 0.9741 0 0
0 0 0 0 0 0 0 0 0.0025 0.1878 0.9048 0
0 0 0 0 0 0 0 0 0 0 0 0.9984
0 0 0 0 0 0 0 0 0 0 0 0.0347
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
Columns 13 through 24
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0.9827 0 0 0 0 0 0 0 0 0 0 0
0 0.9985 0 0 0 0 0 0 0 0 0 0
0 0.0164 0.9918 0 0 0 0 0 0 0 0 0
0 0 0 0.9985 0 0 0 0 0 0 0 0
0 0 0 0.0155 0.9923 0 0 0 0 0 0 0
0 0 0 0 0 0.9984 0 0 0 0 0 0
0 0 0 0 0 0.0278 0.9861 0 0 0 0 0
0 0 0 0 0 0 0 0.9992 0 0 0 0
0 0 0 0 0 0 0 0.0278 0.9861 0 0 0
0 0 0 0 0 0 0 0 0 0.9991 0 0
0 0 0 0 0 0 0 0 0 0.0112 0.9944 0
0 0 0 0 0 0 0 0 0 0 0 0.9988
0 0 0 0 0 0 0 0 0 0 0 0.0093
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
Columns 25 through 33
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0.9953 0 0 0 0 0 0 0 0
0 0.9984 0 0 0 0 0 0 0
0 0.0186 0.9907 0 0 0 0 0 0
0 0 0 0.9989 0 0 0 0 0
0 0 0 0.0127 0.9937 0 0 0 0
0 0 0 0 0 0.9987 0 0 0
0 0 0 0 0 0.0093 0.9953 0 0
0 0 0 0 0 0 0 0.9993 0
0 0 0 0 0 0 0 0.0058 0.9971
Bd =
0.0384 0 0 0
0.0005 0 0 0
0.0000 0 0 0
0 -0.0033 0 0
0 -0.0001 0 0
0 0 0.0384 0
0 0 0.0005 0
0 0 -0.0000 0
0 0 0 0.0384
0 0 0 0.0005
0 0 0 0.0000
0 0.0007 0 0
0 0.0000 0 0
0 0 0.0004 0
0 0 0.0000 0
0 0 0 0.0013
0 0 0 0.0000
-0.0011 0 0 0
-0.0000 0 0 0
0 0.0002 0 0
0 0.0000 0 0
0 0 0.0008 0
0 0 0.0000 0
0 0 0 0.0006
0 0 0 0.0000
-0.0002 0 0 0
-0.0000 0 0 0
0 0.0001 0 0
0 0.0000 0 0
0 0 0.0001 0
0 0 0.0000 0
0 0 0 0.0001
0 0 0 0.0000
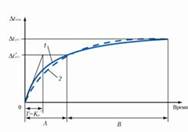
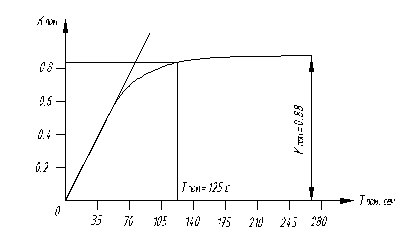
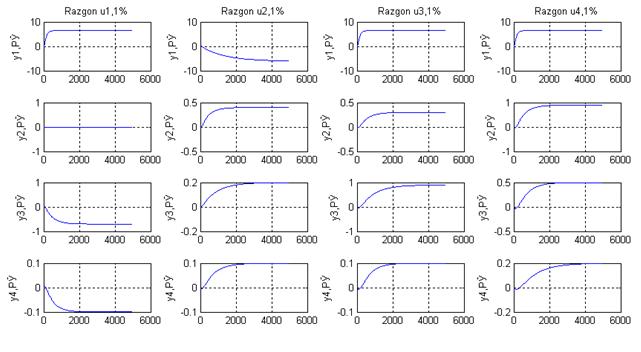Рисунок. Кривые разгона передаточных функций
Если сравнить матрицу передаточных функций и полученные разгонные характеристики(рисунок ), видно, что Кр из матрицы передаточных функций совпадают с Кр на графиках, можно сделать вывод: построение модели и преобразование выполнены верно.
4. Синтез многомерного ПИ-регулятора
Для синтеза ПИ-регулятора полученные матрицы должны быть расширены в матрицы A1, B1, C1:
A1=[Ad zeros(8,2); C eye(2)];
B1=[Bd;zeros(10)];
C1=[C eye(2)];
Матрицы параметров регулятора должны быть рассчитаны с помощью функции dlqr.
K=dlqr(A1,B1,Q,R)
L=dlqr(A1',C1',Q1,R1)'
Расширены матрицы имеют вид:
A1 =
Columns 1 through 12
0.9941 0 0 0 0 0 0 0 0 0 0 0
0.0258 0.9741 0 0 0 0 0 0 0 0 0 0
0.0025 0.1878 0.9048 0 0 0 0 0 0 0 0 0
0 0 0 0.9995 0 0 0 0 0 0 0 0
0 0 0 0.0347 0.9827 0 0 0 0 0 0 0
0 0 0 0 0 0.9941 0 0 0 0 0 0
0 0 0 0 0 0.0258 0.9741 0 0 0 0 0
0 0 0 0 0 -0.0025 -0.1878 0.9048 0 0 0 0
0 0 0 0 0 0 0 0 0.9941 0 0 0
0 0 0 0 0 0 0 0 0.0258 0.9741 0 0
0 0 0 0 0 0 0 0 0.0025 0.1878 0.9048 0
0 0 0 0 0 0 0 0 0 0 0 0.9984
0 0 0 0 0 0 0 0 0 0 0 0.0347
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 -1.0000 1.0000 -1.0000 1.0000 0 -1.0000 -1.0000 0 -1.0000 1.0000 0
0 0 0 0 0 0 0 0 0 0 0 -1.0000
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
Columns 13 through 24
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0.9827 0 0 0 0 0 0 0 0 0 0 0
0 0.9985 0 0 0 0 0 0 0 0 0 0
0 0.0164 0.9918 0 0 0 0 0 0 0 0 0
0 0 0 0.9985 0 0 0 0 0 0 0 0
0 0 0 0.0155 0.9923 0 0 0 0 0 0 0
0 0 0 0 0 0.9984 0 0 0 0 0 0
0 0 0 0 0 0.0278 0.9861 0 0 0 0 0
0 0 0 0 0 0 0 0.9992 0 0 0 0
0 0 0 0 0 0 0 0.0278 0.9861 0 0 0
0 0 0 0 0 0 0 0 0 0.9991 0 0
0 0 0 0 0 0 0 0 0 0.0112 0.9944 0
0 0 0 0 0 0 0 0 0 0 0 0.9988
0 0 0 0 0 0 0 0 0 0 0 0.0093
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
1.0000 -1.0000 1.0000 -1.0000 1.0000 0 0 0 0 0 0 0
0 0 0 0 0 -1.0000 1.0000 -1.0000 1.0000 -1.0000 1.0000 -1.0000
0 0 0 0 0 0 0 0 0 0 0 0
Columns 25 through 36
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0.9953 0 0 0 0 0 0 0 0 0 0 0
0 0.9984 0 0 0 0 0 0 0 0 0 0
0 0.0186 0.9907 0 0 0 0 0 0 0 0 0
0 0 0 0.9989 0 0 0 0 0 0 0 0
0 0 0 0.0127 0.9937 0 0 0 0 0 0 0
0 0 0 0 0 0.9987 0 0 0 0 0 0
0 0 0 0 0 0.0093 0.9953 0 0 0 0 0
0 0 0 0 0 0 0 0.9993 0 0 0 0
0 0 0 0 0 0 0 0.0058 0.9971 0 0 0
0 0 0 0 0 0 0 0 0 1.0000 0 0
0 0 0 0 0 0 0 0 0 0 1.0000 0
1.0000 0 0 0 0 0 0 0 0 0 0 1.0000
0 -1.0000 1.0000 -1.0000 1.0000 -1.0000 1.0000 -1.0000 1.0000 0 0 0
Column 37
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1.0000
B1 =
0.0384 0 0 0
0.0005 0 0 0
0.0000 0 0 0
0 -0.0033 0 0
0 -0.0001 0 0
0 0 0.0384 0
0 0 0.0005 0
0 0 -0.0000 0
0 0 0 0.0384
0 0 0 0.0005
0 0 0 0.0000
0 0.0007 0 0
0 0.0000 0 0
0 0 0.0004 0
0 0 0.0000 0
0 0 0 0.0013
0 0 0 0.0000
-0.0011 0 0 0
-0.0000 0 0 0
0 0.0002 0 0
0 0.0000 0 0
0 0 0.0008 0
0 0 0.0000 0
0 0 0 0.0006
0 0 0 0.0000
-0.0002 0 0 0
-0.0000 0 0 0
0 0.0001 0 0
0 0.0000 0 0
0 0 0.0001 0
0 0 0.0000 0
0 0 0 0.0001
0 0 0 0.0000
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
C1 =
Columns 1 through 20
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Columns 21 through 37
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
K =
1.0e+003 *
Columns 1 through 12
0.0004 0.0064 0.0046 -0.0111 0.0123 0.0006 0.0060 -0.0045 0.0004 0.0060 0.0045 0.0046
0.0006 0.0021 0.0055 -0.0062 0.0107 0.0005 0.0020 -0.0055 0.0007 0.0020 0.0055 0.0148
0.0021 0.0062 0.0043 -0.0115 0.0122 0.0021 0.0068 -0.0043 0.0016 0.0061 0.0043 0.0395
0.0023 0.0057 0.0037 -0.0011 0.0110 0.0021 0.0056 -0.0037 0.0027 0.0064 0.0038 -0.0981
Columns 13 through 24
-0.0165 0.0305 -0.0271 0.0328 -0.0278 -0.0629 -0.0589 -0.0539 -0.0589 0.0373 -0.1078 0.0462
0.0382 -0.0327 0.0614 -0.0367 0.0630 -0.0073 0.0034 -0.0202 0.0034 -0.0268 0.0053 -0.0211
-0.0126 0.0753 -0.0215 0.0795 -0.0221 0.1055 0.0455 0.1545 0.0455 0.0897 0.0883 0.0549
-0.0270 -0.0866 -0.0464 -0.0869 -0.0482 -0.0302 0.0153 -0.0766 0.0153 -0.1052 0.0240 -0.0859
Columns 25 through 36
-0.1173 -0.1704 -0.0363 -0.2339 -0.0512 -0.1978 -0.0673 -0.3134 -0.1028 0.0004 -0.0002 -0.0008
0.0054 0.1627 0.0338 0.2241 0.0479 0.1893 0.0633 0.3033 0.0968 0.0006 0.0007 0.0000
0.0982 -0.5156 -0.0681 -0.7405 -0.1021 -0.6439 -0.1429 -1.0379 -0.2414 0.0004 -0.0002 0.0006
0.0244 0.5344 0.0678 0.7721 0.1016 0.6741 0.1429 1.0857 0.2443 0.0003 -0.0006 0.0002
Column 37
-0.0003
0.0003
-0.0006
0.0006
L =
0.0623 -0.0000 -0.0000 0.0000
0.0771 -0.0000 -0.0000 0.0000
0.2162 -0.0000 -0.0000 0.0000
0.2181 0.0000 -0.0000 -0.0000
0.5175 0.0000 -0.0000 -0.0000
0.0623 -0.0000 0.0000 -0.0000
0.0771 -0.0000 0.0000 -0.0000
-0.2162 0.0000 -0.0000 0.0000
0.0623 0.0000 0.0000 0.0000
0.0771 0.0000 0.0000 0.0000
0.2162 0.0000 0.0000 0.0000
-0.0000 0.1229 0.0000 -0.0000
-0.0000 0.3421 0.0000 -0.0000
-0.0000 0.1079 0.0000 0.0000
-0.0000 0.3455 0.0000 0.0000
0.0000 0.1076 -0.0000 -0.0000
0.0000 0.3482 -0.0000 -0.0000
0.0000 0.0000 0.0789 -0.0000
0.0000 0.0000 0.2349 -0.0000
0.0000 -0.0000 0.1252 -0.0000
0.0000 -0.0000 0.3223 -0.0000
-0.0000 0.0000 0.1000 0.0000
-0.0000 0.0000 0.3037 0.0000
0.0000 0.0000 0.0665 0.0000
0.0000 0.0000 0.2504 0.0000
-0.0000 0.0000 0.0000 0.0709
-0.0000 0.0000 0.0000 0.2282
-0.0000 -0.0000 0.0000 0.0839
-0.0000 -0.0000 0.0000 0.2651
0.0000 -0.0000 0.0000 0.0613
0.0000 -0.0000 0.0000 0.2373
0.0000 0.0000 0.0000 0.0892
0.0000 0.0000 -0.0000 0.3165
1.6703 0.0000 -0.0000 -0.0000
0.0000 1.6189 0.0000 0.0000
-0.0000 0.0000 1.6746 0.0000
-0.0000 0.0000 0.0000 1.6746
5. Моделирование замкнутой системы и оценка качества переходных процессов
Для получения переходных процессов следует сформировать матрицы замкнутой системы и получить переходные процессы с помощью программы dstep.
Ar=[Ad-Bd*K1 -Bd*K2-L1 L1; C eye(2)-L2 L2; zeros(2,8) zeros(2) eye(2)];
Br=[zeros(8,2); zeros(2); eye(2)];
Cr=[-K zeros(2)];
При оценке качества переходных процессов необходимо чтоб отклонение управляющих воздействий не превышало 30% открытия.
Максимальное возмущение следует принять на уровне 10% номинального значения соответствующих параметров. Допустимое значение регулируемых переменных нужно принять равными 20% номинального значения.
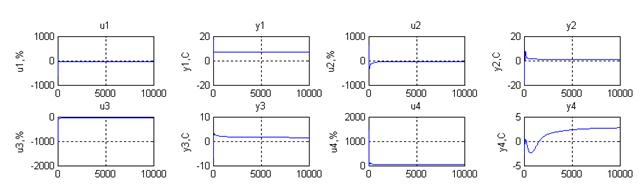
Рисунок. Переходные процессы замкнутосистемы(f=[0.5;05;05;1];z=[7;0.8;1.5;2.8])
Похожие работы
... [3 (п.9.13в)]; - обеспечения минимального расхода наружного воздуха в системах с переменным расходом [3 (п.9.15)] и др. 3.4 Регулирующие функции Регулирующие функции – автоматическое поддержание заданных параметров являются основными по определению [3 (п.9.11)] для систем воздушного отопления, приточной и вытяжной вентиляции, работающей с переменным расходом, рециркуляцией воздуха, систем ...
... К. Сатпаева» для просмотра и ввода информации системы оперативно-диспетчерского контроля и управления, создаваемые на Visual Basic. Специфика используемого в системе оперативно-диспетчерского контроля и управления РГП «Канал им. К. Сатпаева» ПО такая, что разработка ПО, как таковая, может производиться только при создании самой системы. Применяемое ПО является полуфабрикатом. Основная задача ...
... А вот традиционные центральные системы кондиционирования надо закладывать в проект еще на стадии строительства. Благодаря целому ряду уникальных достоинств VRV системы составили серьезную конкуренцию традиционным центральным системам кондиционирования воздуха, а в ряде стран, например в Японии, практически полностью вытеснили их с рынка. Конечно, на этом прогресс в развитии климатической техники ...
... управления осуществляется с помощью автоматизированного модуля верхнего уровня, который также отвечает за интерфейс на посту оператора. 3.1 Требования к структуре системы Автоматизированная система управления и контроля климата в тепличных хозяйствах выполнена на базе микропроцессорной техники. По иерархическому принципу АСУ ККТХ должна подразделяться на уровни: нижний уровень: - ...
0 комментариев