Алгоритм и его структура

Оглавление

Введение

Глава 1. Алгоритм и его свойства. Способы записи алгоритма

Глава 2. Классификация алгоритмов

2.1 Линейная алгоритмическая структура. Типовые примеры

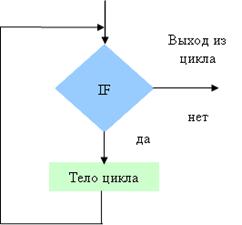
2.2 Разветвляющая алгоритмическая структура. Основные операторы циклов. Типовые примеры

2.3 Циклические алгоритмические структуры. Основные операторы ветвления. Типовые примеры

Глава 3. Языки программирования

3.1 Интерпретаторы

3.2 Компиляторы

3.3 Эволюция и классификация языков программирования

Заключение

Список литературы

Введение

Применение компьютерных технологий в различных сферах современного общества станет значительно эффективнее, если пользователи овладеют системным подходом в решении прикладных задач, будут иметь представление о методах разработки алгоритмов и составления программ, а значит - о компьютеризации различных видов деятельности.

Процессор электронно-вычислительной машины, это чудо техники, умеет, тем не менее, выполнять лишь простейшие команды. Каким же образом компьютер решает сложнейшие задачи обработки информации? Для решения этих задач программист должен составить подробное описание последовательности действий, которые необходимо выполнить центральному процессору компьютера.

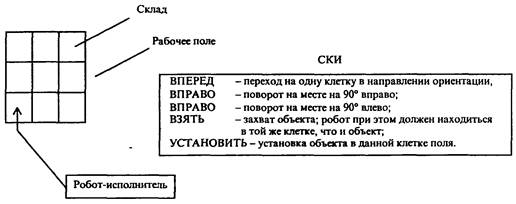
Составление такого пошагового описания процесса решения задачи называется алгоритмизацией, а алгоритмом называется конечный набор правил, расположенных в определённом логическом порядке, позволяющий исполнителю решать любую конкретную задачу из некоторого класса однотипных задач. В разных ситуациях в роли исполнителя может выступать электронное или какое-либо иное устройство или человек (например, военнослужащий, охраняющий склад боеприпасов и действующий согласно алгоритмам, записанным в устав караульной службы).

Глава 1. Алгоритм и его свойства. Способы записи алгоритма

Само слово «алгоритм» возникло из названия латинского перевода книги арабского математика IX века Аль-Хорезми «Algoritmi de numero Indoru», что можно перевести как «Трактат Аль-Хорезми об арифметическом искусстве индусов». Составление алгоритмов и вопросы их существования являются предметом серьёзных математических исследований.

Под алгоритмом понимают набор правил, определяющих процесс преобразования исходных данных задачи в искомый результат.

Рассмотрим пример алгоритма для нахождения середины отрезка при помощи циркуля и линейки.

Алгоритм деления отрезка АВ пополам:

1) поставить ножку циркуля в точку А;

2) установить раствор циркуля равным длине отрезка АВ;

3) провести окружность;

4) поставить ножку циркуля в точку В;

5) провести окружность;

6) через точки пересечения окружностей провести прямую;

7) отметить точку пересечения этой прямой с отрезком АВ.

Анализ примеров различных алгоритмов показывает, что запись алгоритма распадается на отдельные указания исполнителю выполнить некоторое законченное действие. Каждое такое указание называется командой. Команды алгоритма выполняются одна за другой. После каждого шага исполнения алгоритма точно известно, какая команда должна выполнятся следующей. Совокупность команд, которые могут быть выполнены исполнителем, называется системой команд исполнителя.

Алгоритм не только задает последовательность выполнения операций при решении конкретной задачи, но и должен обладать рядом свойств.

Свойства алгоритма:

·                   Однозначность алгоритма, под которой понимается единственность толкования исполнителем правила построения действий и порядок их выполнения. Чтобы алгоритм обладал этим свойством, он должен быть записан командами из системы команд исполнителя.

·                   Конечность алгоритма – обязательность завершения каждого из действий, составляющих алгоритм, и завершимость выполнения алгоритма в целом.

·                   Результативность алгоритма, предполагающая, что выполнение алгоритма должно завершиться получением определённых результатов.

·                   Массовость, т. е. возможность применения данного алгоритма для решения целого класса задач, отвечающих общей постановке задачи. Для того чтобы алгоритм обладал свойством массовости, следует составлять алгоритм, используя обозначения величин и избегая конкретных значений.

·                   Правильность алгоритма, под которой понимается способность алгоритма давать правильные результаты решения поставленных задач.

·                   Эффективность – для решения задачи должны использоваться ограниченные ресурсы компьютера (процессорное время, объём оперативной памяти и т. д.).

Создание алгоритма для решения задач какого-либо типа, его представление исполнителю в удобной для него форме – это творческий акт.

Алгоритм может быть представлен различными способами:

·                   на разговорном, естественном языке;

·                   на языке блок-схем;

·                   на языке программирования.

Выбор и разработка алгоритма и численного метода решения задачи имеют важнейшее значение для успешной работы над программой. Тщательно проработанный алгоритм решения задачи – необходимое условие эффективной работы по составлению алгоритму.

Приведем пример записи алгоритма на естественном языке, то есть на языке человеческого общения. Требуется вычислить сумму двух чисел. Обозначим эти числа a и b. Тогда алгоритм можно записать следующим образом:

1. Считать число a.

2. Считать число b.

3. Выполнить суммирование c := a + b.

4. Вывести число c.

Видно, что формулировка алгоритма не зависит от конкретных значений переменных a и b, поэтому его можно применять для решения достаточно большого числа сходных задач, в данном случае вместе составляющих целый класс задач суммирования. Алгоритм описывает действия не над конкретными значениями, а над абстрактными объектами.

Основными объектами программирования являются переменные. Переменные в программе отличаются от переменных, используемых в записи математических формул. Несмотря на сходство терминов, правила использования переменных в программах для компьютера отличаются от правил работы с математическими переменными. Это различие необходимо уяснить. В программировании переменную можно трактовать как одну или несколько ячеек оперативной памяти компьютера, которым присвоено определённое имя. Содержимое этих ячеек может меняться, но имя переменной остаётся неизменным. В математике значение переменной в рамках определённой задачи неизменно, но меняется в других задачах из данного класса. Именно поэтому конструкция а := а + 1 воспринимается программистом совершенно естественно, а уравнение a = a + 1 математик сочтёт неверным. В первом случае имеется в виду вычисление суммы содержимого ячейки а и числовой константы 1 и занесение полученного результата в ту же ячейку а. Второй случай равносилен неверному тождеству 0 = 1.

Иногда используют полуформальный язык с ограниченным словарём (часто на основе английского языка), промежуточный между естественным языком и языком программирования. Такой язык называется псевдокодом. Запись алгоритма на псевдокоде называется структурным планом. Псевдокод удобен тем, что позволяет программисту сосредоточиться на формулировке алгоритма, не задумываясь над синтаксическими особенностями конкретного языка программирования.

Псевдокод:

Алгоритм < название >

Начало

< последовательность действий >

Конец

Любой алгоритм может быть представлен в виде последовательности действий. Под действием понимают либо базовую операцию, либо базовую структуру.

В качестве базовых операций используются:

·                   операция присваивания вида

< переменная > := < выражение >

·                   операция ввода/вывода

ввод ( список ввода)

вывод ( список вывода).

Смысл операции присваивания состоит в вычислении результата выражения, стоящего справа от знака «:=», для конкретных значений входящих в него переменных и присваивании этого результата переменной, стоящей слева от знака «:=», например:

D := 5

D := D+1

Min := C

При выполнении операции ввода ввод ( A, B, C) переменным из списка ввода A, B и C присваиваются конкретные значения, вводимые с клавиатуры, например:

-5 7 20 {Enter}

В результате в памяти получим:

A = -5, B = 7, C = 20.

Операция вывода осуществляет вывод значений переменных и выражений из списка вывода на экран, например:

вывод (A, B, C, 10)

На экране получим:

- 5 7 20 10

Описание алгоритмов с помощью блок-схем.

Для разработки структуры программы удобнее пользоваться записью алгоритма в виде блок-схемы (в англоязычной литературе используется термин flow-chart). Для изображения основных алгоритмических структур и блоков на блок-схемах используют специальные графические символы.

Составим алгоритм вычисления квадратного корня из произвольного положительного вещественного числа х в виде блок-схемы.

Блок-схема для решения данного рода задач будет выглядеть следующим образом:

Начало

Ввод вещественного числа х

Вычисление корня по формуле

Вывод результата

Конец

Глава 2. Классификация алгоритмов

Различают три типа базовых структур:

·                   Следование

·                   Развилка

·                   Цикл

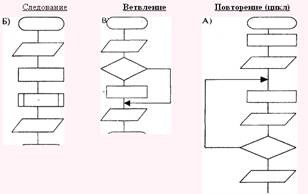
Структура Следование - одна из самых важных структур. Она означает, что два действия должны быть выполнены друг за другом.

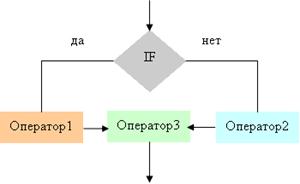
Структура Развилка обеспечивает выбор одной из двух альтернатив: если < условие 1 > то

< действие 1 >

иначе

< действие 2 >

все

Существует сокращенная форма структуры Развилка, которая позволяет выполнить действие или пропустить его:

если < условие > то < действие >

все

Обобщением структуры Развилка является Множественный выбор:

если Var = Const1 то < действие 1 >

если Var = Const2 то < действие 2 >

если Var = ConstN то < действие N >

все

В зависимости от значения переменной Var выполняется одно из указанных действий, например, если Var = Const3, то выполняется < действие 3 >.

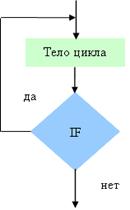
Третьей базовой структурой является Цикл, который предусматривает повторное выполнение определенных действий, необходимое для большинства программ. Различают следующие типы структур Цикл:

·                   цикл «от до»

·                   цикл «пока»

·                   цикл «до»

Цикл «от до» управляет повторением выполнения действия с помощью переменной цикла:

цикл от I:= N1 до N2

< действие >

кц

Здесь I - переменная цикла, N1, N2 - начальное и конечное значения переменной цикла, вычисляются один раз при входе в цикл. Переменная цикла пробегает все следующие друг за другом в порядке возрастания значения от начального до конечного. Изменение значения переменной цикла происходит автоматически после каждого выполнения действия, указанного внутри цикла. В зависимости от соотношения N1 и N2 цикл может не выполниться ни разу (N1>N2) или выполниться (N2-N1+1) раз.

В цикле «пока» управление внутри цикла осуществляется с помощью логического условия:

цикл пока < условие>

< действие >

кц

Выполнение действия повторяется до тех пор, пока истинно условие. Проверка условия осуществляется в начале цикла. Это означает, что действие может не выполниться ни разу. Чтобы такой цикл не был бесконечным, внутри цикла необходимо предусмотреть изменение значения условия с истинного на ложное.

Третий тип структуры цикл «до» имеет вид:

цикл

< действие > до < условие>

кц

Как только значение условия становится истинным, цикл прекращается. Цикл “до“ независимо от значения условия выполнится по меньшей мере один раз, т.к. проверка условия производится после выполнения действия. Для завершения цикла необходимо внутри цикла изменить условие с ложного на истинное. Выбор структуры цикла определяется особенностями алгоритма решения конкретной задачи.

Существенная особенность перечисленных базовых структур состоит в том, что каждая из них имеет один вход и один выход. Их можно соединять друг с другом в любой последовательности. В качестве действия может использоваться любая из перечисленных структур, что обеспечивает возможность вложенности одних структур в другие.

В зависимости от применяемых базовых структур различают следующие типы алгоритмов:

·                   линейные

·                   разветвляющиеся

·                   циклические.

2.1 Линейная алгоритмическая структура. Типовые примеры

Линейным называется алгоритм, блоки которого расположены последовательно один за другим, нет условий и повторений.

Покажем общую структуру линейного алгоритма в виде блок-схемы.

Основной принцип программирования заключается в том, что обрабатывать можно только те данные, которые находятся в определенных областях оперативной памяти компьютера. Для того чтобы поместить исходные данные в оперативную память используются операторы ввода данных.

Для реализации процесса обработки данных используется оператор присваивания.

Результат вычислений помещается в область S оперативной памяти. Чтобы вывести результат из памяти на экран монитора необходимо использовать оператор вывода.

Операторы ввода данных:

1.                INPUT - оператор ввода данных с клавиатуры. Данные задаются в виде переменных. Переменная – это величина, значение которой может меняться в процессе выполнения программы. Для обозначения переменной используются их имена (идентификаторы) – последовательность до 40 латинских букв и цифр, начинающаяся с буквы. Данные могут быть следующих основных типов:

·                   целые INTEGER (Y%) – 2 байта в памяти (от -32768 до 32767),

·                   длинные целые LONG (Y&) – 4 байта (от -2³¹ до 2³¹-1),

·                   вещественные SINGLE (Y) – 6 знаков после , -4 байта (от -3.4Е+38 до 3.4Е+38),

·                   вещественные удвоенной точности DOUBLE (Y#) -16 знаков после ,– 8 байт (от -Е+308 до Е+308),

·                   символьные STRING (Y$) – последовательность символов до 32767 символов длиной.

Например: INPUT a,b или INPUT “Введите два числа”;a,b