Математико-статистические методы анализа и прогнозирования демографической ситуации в РБ

3. Математико-статистические методы анализа и прогнозирования демографической ситуации в РБ

3.1 Корреляционно-регрессионный анализ факторов, влияющих на демографическую ситуацию в РБ

Оценить вид и степень зависимости демографического поведения населения Бурятии, определяющего демографическую ситуацию в республике, от социально-экономической ситуации можно с помощью методов корреляции и регрессии.

Корреляционный метод дает возможность количественно оценивать связи между исследуемыми явлениями в условиях действия большого числа факторов, часть которых неизвестна. С его помощью осуществляется проверка экономико-демографических гипотез о наличии, силе и форме связи между переменными.

С помощью регрессионного метода можно определить степень влияния каждого фактора на результативный признак. Одновременно проводится оценка степени такого влияния с помощью различных критериев [24, с. 36].

В данном исследовании была поставлена задача - исследовать демографические процессы в республике Бурятия, выявить факторы, влияющие на интенсивность рождаемости, смертности и миграции. Анализ этих зависимостей основывался на изучении данных за последние 13 лет (1995-2007 гг.).

Изменения численности населения, в основном, определяются динамикой трех демографических процессов - рождаемости, смертности и миграции. Среди компонент изменения численности населения уровень смертности является наиболее чувствительным индикатором изменения качества жизни, тогда как динамика рождаемости нередко опосредована достаточно инертными стереотипами репродуктивного поведения населения, а уровень миграции отражает не столько изменения качества жизни населения на определенной территории, сколько его относительные изменения относительно других территорий. Исходя из этого, необходимо проанализировать причины и факторы, влияющие на интенсивность всех трех процессов.

Чтобы определить, от каких факторов зависят величины рождаемости, смертности и миграции, необходимо построить регрессионную модель на основании следующих показателей: в качестве результативных признаков были взяты - общие коэффициенты рождаемости и смертности и уровень миграции (коэффициент миграционного прироста на 10 000 жителей) – У₁ У₂, У₃. Факторные признаки были рассмотрены следующие:

X₁ - доля детей до 15 лет (в % от общей численности населения),

Х₂ - доля лиц пенсионного возраста (в % от общей численности населения),

Х_З - показатель уровня жизни населения (соотношение доходов и прожиточного минимума, ед.),

Х₄ - показатель обеспеченности жильем (м² на 1 человека),

Х₅ - уровень миграции (коэффициент миграционного прироста на 10 000 жителей),

Х₆ - заболеваемость (% заболевших за год от общей численности населения),

Х₇ - доля безработных (в % к от экономически активного населения).

Исходя из экономической сущности изучаемых факторных признаков, можно сказать, что причинная связь наблюдается между всеми результативными и факторными признаками. При построении моделей, описывающих рождаемость и смертность, показатели миграции используются как факторный признак.

Эти факторные признаки были взяты неслучайно, так как большинство из них в разных комбинациях использовали многие ученые, занимающиеся прогнозами и исследованиями демографических процессов, а также их взаимовлиянием. Можно упомянуть модель межрайонного оттока В.Л. Лысенко (установлена зависимость миграции от обеспеченности жильем и учреждениями просвещения), модель В.Д. Зайцева (миграция зависит от уровня оплаты труда, возможности трудоустройства и обеспеченности жильем), в модели В.А. Глазова получены данные, что наибольшее влияние на демографическую ситуацию оказывают экономические факторы (размеры капитальных вложений, прирост рабочих мет и уровень заработной платы) и в значительно меньшей степени социально-бытовые факторы (уровень развития медицины, обеспеченность жильем).

Нами был проведен корреляционный и регрессионный анализ с помощью пакета Excel. Анализ вариационных характеристик, полученных от каждой переменной, показал, что они свидетельствуют о подчинении изучаемых признаков нормальному закону распределения, что является немаловажным условием для проведения дальнейшего анализа.

Следующим этапом предварительного анализа является анализ матрицы парных коэффициентов корреляции - характеризуют связь между двумя признаками без учета влияния других факторов. Здесь можно выдвинуть гипотезу о взаимозависимости признаков, что может негативно сказаться на проведении анализа. Анализируя матрицу парных коэффициентов корреляции, можно сказать, что значимы все коэффициенты корреляции между исследуемыми признаками. Анализ также показал наличие почти функциональной прямой зависимости между X₁ (доля детей до 15 лет) и Х₅ (уровень миграции) и обратной почти функциональной зависимости между Х₁ и Х₄ парные коэффициенты корреляции равны 0,87 и -0,97 соответственно.

Результат представлен в таблице 23.

Таблица 23. Матрица парных коэффициентов корреляции

	У1	У2	Х1	Х2	Х3	Х4	Х5	Х6	Х7
У1	1		-0,78	-0,18	0,85	0,86	-0,41	0,69	-0,44
У2		1	-0,90	0,15	0,74	0,95	-0,66	0,61	-0,42
Х1	-0,78	-0,90	1	-0,41	-0,73	-0,97	0,87	-0,34	0,10
Х2	-0,18	0,15	-0,41	1	-0,15	0,28	-0,68	-0,51	0,36
Х3	0,85	0,74	-0,73	-0,15	1	0,79	-0,51	0,51	-0,13
Х4	0,86	0,95	-0,97	0,28	0,79	1	-0,79	0,49	-0,20
Х5	-0,41	-0,66	0,87	-0,68	-0,51	-0,79	1	-0,01	-0,22
Х6	0,69	0,61	-0,34	-0,51	0,51	0,49	-0,01	1	-0,43
Х7	-0,44	-0,42	0,10	0,36	-0,13	-0,20	-0,22	-0,43	1

С помощью пакета Excel были построены регрессионные уравнения, включающие все исходные показатели. Проверка гипотезы о нормальном распределении показала, что с доверительной вероятностью 0,95 их можно считать нормально распределенными.

Общие формулы модели имеют вид:

ŷ ₁ = a_o+aх_i+....a_mх_m

ŷ₂ = a_o+aх_i+....a_mх_m

ŷ₃ = a_o+aх_i+....a_mх_m-i

В данных уравнениях ŷ_1…3 - зависимые переменные, x_ij - объясняющие переменные, а ij = i,m - коэффициенты при независимых переменных, m - число коэффициентов.

Уравнение, характеризующее рождаемость имеет вид:

ŷ ₁ = 23,9-0,36х₁-0,84x₂+0,005x₃+0,63х₄+0,035х₅-0,005х₆-0,002х₇

Рассмотрим параметры адекватности уравнения регрессии:

Множественный коэффициент детерминации равен 0,98, что показывает очень сильную зависимость между результативным признаком и факторными. Стандартная ошибка равна 0,23. F_набл. =26,8 можно сказать, что уравнение регрессии значимо, так как F _набл.> F _кр. (при n =13; α=0,95; ν₁ = 7; ν₂ =3) = 4,35, то есть хотя бы один коэффициент регрессии не равен нулю.

Для проверки значимости отдельных коэффициентов регрессии сравним критическое значение t=2,26 с t_j.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа с исключением переменных. Исключаем величину, имеющую минимальное значение

t =-0,05. (х₇).

Для оставшихся переменных получим уравнение регрессии:

ŷ ₁= 23,9-0,36 х₁-0,86х₂+0,005х₃+0,65х₄+0,03х₅-0,0005х₆

Рассмотрим параметры адекватности уравнения регрессии:

Множественный коэффициент детерминации равен 0,98, что показывает очень сильную зависимость между результативным признаком и факторными. Стандартная ошибка равна 0,2. F _набл. =41,7 можно сказать, что уравнение регрессии значимо, так как F набл.> F кр. (при n =13; α=0,95; ν₁ = 6; ν₂ =4) = 4,53, то есть хотя бы один коэффициент регрессии не равен нулю.

Для проверки значимости отдельных коэффициентов регрессии сравним критическое значение t=2,26 с t_j, получим, что в уравнении не все коэффициенты регрессии значимы.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа с исключением переменных. Исключаем величину, имеющую минимальное значение

t =-0,19. (х₆).

Для оставшихся переменных получим уравнение регрессии:

ŷ ₁=23,5- 0,38 х₁-0,76х₂+0,006х₃+0,58х₄+0,03х₅

Рассмотрим параметры адекватности уравнения регрессии:

Множественный коэффициент детерминации равен 0,98, что показывает очень сильную зависимость между результативным признаком и факторными. Стандартная ошибка равна 0,18. F _набл. =61,96 можно сказать, что уравнение регрессии значимо, так как F _набл.> F _кр, (при n=13; α=0,95; ν₁ = 5; ν₂ =5) = 5,05, то есть хотя бы один коэффициент регрессии не равен нулю.

Для проверки значимости отдельных коэффициентов регрессии сравним критическое значение t=2,26 с t_j, получим, что в уравнении не все коэффициенты регрессии значимы.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа с исключением переменных. Исключаем величину, имеющую минимальное значение t =0,88 (х₃).

ŷ ₁=28,3- 0,39 х₁-1,06х₂+0,63х₄+0,03х₅

Это уравнение регрессии удачно аппроксимирует фактическое значение рождаемости, так как ошибка аппроксимации равна всего 0,17%, а значения остатков очень малы.

Высокий уровень множественного коэффициента детерминации =0,98 свидетельствует, что 99% вариации результативной переменной описывается вошедшими в модель признаками. Остальная часть вариации описывается неучтенными факторами.

Коэффициент Дарбина-Уотсона = 1,85, то есть близок к 2, что свидетельствует о незначительной автокорреляции в остатках и подтверждает адекватность построенной модели.

В уравнении при изменении каждого фактора на 1 единицу собственного измерения зависимая переменная изменяется на соответствующий коэффициент регрессии, то есть коэффициент регрессии β_j отражает приращение функции за счет единичного приращения j-ro аргумента, независимое от остальных учтенных в модели аргументов. Интерпретируемый таким образом коэффициент регрессии используется в экономико-статистическом анализе для сравнения оценки влияния j-ro аргумента на функцию.

Анализируя полученную модель можно сказать, что при повышении доли лиц пенсионного возраста на 1% рождаемость уменьшится на 1,06 родившегося на 1000 (так как коэффициент отрицательный) и при увеличении обеспеченности жильем на 1 м² общей площади на 1 человека рождаемость увеличится на 0,63. Столь парадоксальный факт можно объяснить тем, что в связи с большим выездом в регионе значительно улучшилось положение с жильем. То есть рождаемость продолжала падать, а жилплощадь высвобождалась - это объясняется последствиями экономического кризиса.

Рассматривая полученное уравнение, можно отметить, что в основном рождаемость определяется таким фактором как доля лиц пенсионного возраста, а также обеспеченностью жильем. Миграция и доля детей в населении имеют некоторую обратную связь с рождаемостью, но очень заметного влияния не оказывают. Из этого можно сделать следующий вывод - проблемы с рождаемостью в республике Бурятия обусловлены в первую очередь снижением доли лиц молодого возраста, на что и требуется обратить пристальное внимание. Необходимо следить за выполнением федерально-целевых программ. Реализация репродуктивной функции тесно связана с экономическим и социальным положением населения.

Уравнения зависимости показателя смертности имеют следующий вид:

ŷ₂ = 5,54-0,25х₁ + 0,13х₂-0,002х₃ +0,74х₄-0,002х₅+0,005х₆-0,14х₇

Рассмотрим параметры адекватности уравнения регрессии:

Множественный коэффициент детерминации равен 0,97, что показывает очень сильную зависимость между результативным признаком и факторными. Стандартная ошибка равна 0,46. F _набл. =16,03 можно сказать, что уравнение регрессии значимо, так как F _набл.> F _кр. (при n=13; α=0,95; ν₁ = 7; ν₂ =3) = 4,35, то есть хотя бы один коэффициент регрессии не равен нулю.

Для проверки значимости отдельных коэффициентов регрессии сравним критическое значение t=2,26 с t_j.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа с исключением переменных. Исключаем величину, имеющую минимальное значение

t =-0,088 (х₅).

Для оставшихся переменных получим уравнение регрессии:

ŷ₂ = 4,73-0,26х₁+0,19х₂-0,002х₃+0,75х₄ +0,005х₆-0,14х₇

Множественный коэффициент детерминации равен 0,97, что показывает очень сильную зависимость между результативным признаком и факторными. Стандартная ошибка равна 0,4. F _набл. =24,87. Можно сказать, что уравнение регрессии значимо, так как F _набл.> F _кр. (при n =13; α=0,95; ν₁ = 6; ν₂ =4) = 4,53, то есть хотя бы один коэффициент регрессии не равен нулю.

Для проверки значимости отдельных коэффициентов регрессии сравним критическое значение t=2,26 с t_j.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа с исключением переменных. Исключаем величину, имеющую минимальное значение t =-0,099 (х₃).

Для оставшихся переменных формируем уравнение регрессии снова:

ŷ₂= 3,71-0,27х₁+0,31х₂+0,68х₄+0,005х₆-0,15х₇

Множественный коэффициент детерминации равен 0,97, что показывает очень сильную зависимость между результативным признаком и факторными. Стандартная ошибка равна 0,36. F _набл. =37,21. Можно сказать, что уравнение регрессии значимо, так как F _набл.> F _кр. (при n=13; α=0,95; ν₁ = 5; ν₂ =5) = 5,05, то есть хотя бы один коэффициент регрессии не равен нулю.

Для проверки значимости отдельных коэффициентов регрессии сравним критическое значение t=2,26 с t_j.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа с исключением переменных. Исключаем величину, имеющую минимальное значение t =0,44 (х₂).

Получим следующее уравнение: ŷ₂= 9,16-0,29х₁+0,7х₄+0,004х₆-0,14х₇.

Множественный коэффициент детерминации равен 0,97, что показывает очень сильную зависимость между результативным признаком и факторными. Стандартная ошибка равна 0,33. F _набл. =53,7. Можно сказать, что уравнение регрессии значимо, так как F _набл.> F _кр. (при n=13; α=0,95; ν₁ = 4; ν₂ =6) = 6,16, то есть хотя бы один коэффициент регрессии не равен нулю.

Для проверки значимости отдельных коэффициентов регрессии сравним критическое значение t=2,26 с t_j.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа с исключением переменных. Исключаем величину, имеющую минимальное значение t =-0,9 (х₁).

Получим следующее уравнение: ŷ₂= -6,83+1,29х₄+0,002х₆-0,13х₇.

Это уравнение регрессии удачно аппроксимирует фактическое значение рождаемости, так как ошибка аппроксимации равно всего 0,33%, а значения остатков очень малы.

Высокий уровень множественного коэффициента детерминации = 0,97 свидетельствует, что 97% вариации результативной переменной описывается вошедшими в модель признаками. Остальная часть вариации описывается неучтенными факторами.

Коэффициент Дарбина-Уотсона =1,83, то есть близок к 2, что свидетельствует о незначительной автокорреляции в остатках и подтверждает адекватность нашей модели.

Анализируя полученную модель можно сказать, что при увеличении обеспеченности жильем на 1 кв.м. общей площади на 1 чел. смертность увеличится на 1,29‰. Это можно объяснить тем, что в связи с усилением миграционного оттока в регионе значительно улучшилось положение с жильем, а смертность выросла из-за экономического кризиса. Уравнение смертности интерпретировать несколько сложнее, чем уравнения зависимости рождаемости. При увеличении безработицы на 1% смертность снизится на 0,13‰. Как ни странно, но заболеваемость практически не влияет на уровень смертности населения. Это можно объяснить тем, что много людей погибает в большинстве от несчастных случаев.

При рассмотрении уравнений зависимости миграции от перечисленных факторных признаков было получено следующее соотношение: ŷ₃ = 334,8 +3,5х₁-20,9х₂-0,03х₃-7,05х₄+0,03х₆ -1,61х₇.

Рассмотрим параметры адекватности уравнения регрессии:

Множественный коэффициент детерминации равен 0,92, что показывает сильную зависимость между результативным признаком и факторными. Стандартная ошибка равна 0,52. F _набл. =7,4. Можно сказать, что уравнение регрессии значимо, так как F набл.> F кр. (при n =13 α=0,95; ν₁ = 6; ν₂ =4) = 4,53, то есть хотя бы один коэффициент регрессии не равен нулю.

Для проверки значимости отдельных коэффициентов регрессии сравним критическое значение t=2,26 с t_j.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа с исключением переменных. Исключаем величину, имеющую минимальное значение t =-0,06 (х₃).

Для оставшихся переменных получим уравнение регрессии:

ŷ₃= 321,3+3,4х₁ - 19,3х₂ – 7,9х₄+0,03х₆ – 1,67х₇.

Рассмотрим параметры адекватности уравнения регрессии:

Множественный коэффициент детерминации равен 0,92, что показывает сильную зависимость между результативным признаком и факторными. Стандартная ошибка равна 0,6. F _набл. =11,1. Можно сказать, что уравнение регрессии значимо, так как F _набл.> F _кр. (при n=13; α=0,95; ν₁ = 5; ν₂ =5) = 5,05, то есть хотя бы один коэффициент регрессии не равен нулю.

Для проверки значимости отдельных коэффициентов регрессии сравним критическое значение t=2,26 с t_j.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа с исключением переменных. Исключаем величину, имеющую минимальное значение t =0,36 (х₆).

Получили следующее уравнение: ŷ₃=303,5+4,57х₁–22,5х₂–4,69х₄–1,67х₇.

Рассмотрим параметры адекватности уравнения регрессии:

Множественный коэффициент детерминации равен 0,91, что показывает сильную зависимость между результативным признаком и факторными. Стандартная ошибка равна 0,5. F _набл. =16,2. Можно сказать, что уравнение регрессии значимо, так как F _набл.> F _кр. (при n=13; α=0,95; ν₁ = 4; ν₂ =6) = 6,16, то есть хотя бы один коэффициент регрессии не равен нулю.

Для проверки значимости отдельных коэффициентов регрессии сравним критическое значение t=2,26 с t_j.

Для получения уравнения регрессии со значимыми коэффициентами используем пошаговый алгоритм регрессионного анализа с исключением переменных. Исключаем величину, имеющую минимальное значение t =-0,41 (х₄).

Имеем следующее уравнение: ŷ₃= 130,5 + 7,05х₁-20,3х₂-11,5х₇.

Это уравнение регрессии удачно аппроксимирует фактическое значение рождаемости, так как ошибка аппроксимации равно всего 0,32%, а значения остатков очень малы.

Высокий уровень множественного коэффициента детерминации =0,91 свидетельствует, что 91% вариации результативной переменной описывается вошедшими в модель признаками. Остальная часть вариации описывается неучтенными факторами.

Коэффициент Дарбина-Уотсона = 1,87, то есть приближается к 2, что свидетельствует о незначительной автокорреляции в остатках и подтверждает адекватность нашей модели.

Анализируя полученную модель можно сказать, что при повышении доли лиц пенсионного возраста на 1% сальдо миграции уменьшится на 20,3 на 1000 (так как коэффициент отрицателен) и при уменьшении безработицы на 1% сальдо миграции уменьшится на 11,5 чел. на 1000.

Влияние на миграционные процессы в республике оказывают экономические причины – показатели безработицы. Требуется обратить внимание на создание благоприятных условий для активной жизнедеятельности человека в регионе. Необходимо вводить более высокие нормативы при развитии социальной инфраструктуры по сравнению с центральными частями России и даже с учетом различий внутри рассматриваемых субъектов.

Основной причиной оттока населения из региона является текучесть кадров из-за низкой заработной платы. Также на этой территории большое значение на миграцию оказывает возрастная структура населения: причем в большинстве случаев не только увеличение пожилого населения, но и детского усиливает отток.

Можно сделать общий вывод, исходя из всех рассмотренных моделей, что наибольшее значение на процессы рождаемости, смертности и миграции в регионе оказывает экономический фактор и только за счет улучшения положения населения можно добиться стабилизации демографической ситуации.

3.2 Прогнозирование основных составляющих демографической ситуации: рождаемости и смертности

Для разработки прогноза показателей естественного движения населения нами использован метод экспоненциального сглаживания. Он заключается в том, что уровни исходного временного ряда взвешиваются с помощью скользящей средней, веса которой подчиняются экспоненциальному закону распределения. Данная скользящая средняя получила название экспоненциальной средней S_t (y) и позволяет проследить закономерности изменения явления в динамике по наиболее существенным последним уровням.

Особенность метода заключается в том, что при расчете теоретических значений, полученных по модели тренда, учитываются только значения предыдущих уровней временного ряда взятых с определенным весом [21, с. 94].

Общая формула расчета экспоненциальной средней:

S_t (y)= α*у_t + (1 – α)* S_t-1 (y),

где S_t (y) – значение экспоненциальной средней временного ряда для момента t;

S_t-1 (y) – значение экспоненциальной средней для момента t – 1;

у_t– значение последнего уровня ряда динамики для перспективного прогнозирования или значение уровня временного ряда социально-экономического явления в момент t;

α – параметр сглаживания (вес t-го значения уровня временного ряда.

При вычислении экспоненциальной средней используются значения предыдущей экспоненциальной средней и значения последнего уровня временного ряда, все предыдущие уровни ряда опускаются.

Одной из проблем практической реализации этого метода является определение значения параметра сглаживания α. От значения параметра α зависят веса предшествующего значения временного ряда и в соответствии с этим степень их влияния на сглаживаемый уровень, а, следовательно, и значение прогнозных оценок. Автор метода Р.Г.Браун предложил следующую формулу расчета α = 2/(n+1), где n – число уровней временного ряда вошедших в интервал сглаживания.

В нашем случае α = 0,167, так как число уровней временного ряда равно 11.

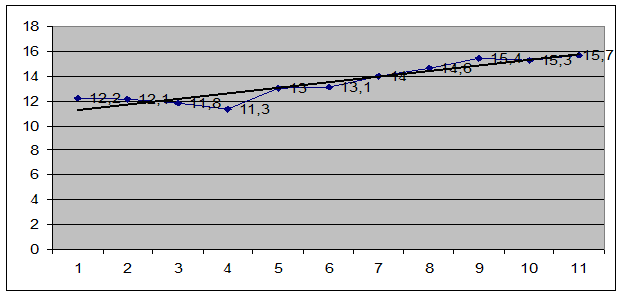
Рисунок 3.1 - Тенденция исходного временного ряда показателя уровня рождаемости

Тенденция исходного временного ряда описывается линейным трендом, что видно на рисунке 3.1.

Получили уравнение вида: ŷ_t = 10,79 – 0,257*t

Теперь определим начальные условия первого и второго порядков. Порядок начального условия определяется числом параметров линейного тренда.

Начальное условие первого порядка: S₀¹(y)=9,51;

начальное условие второго порядка: S₀²(y)= 8,23.

Следующим этапом является расчет экспоненциальных средних первого и второго порядков.

Экспоненциальная средняя первого порядка S_t¹(y)=12,7.

Экспоненциальная средняя второго порядка S_t²(y)= 8,97.

Прогноз строится по модели вида ŷ*_t+L = â₀ + â₁* t,

где t =1;

â₀ = 16,43;

â₁ = 0,746.

Сделаем прогноз на 2008 год, где t = 3, так как последний уровень ряда 2005 года.

ŷ*_3+L= 16,43 + 0,746*3;

ŷ*_3+L= 18,668.

Прогноз на 2009 год: ŷ*_4+L= 19,414.

По проделанным расчетам можно сказать, что в 2008 году коэффициент рождаемости будет равен 18,7 промилле, а в 2009 году – 19,4 промилле.

Спрогнозируем уровень смертности.

α = 0,167, так как число уровней временного ряда равно 11.

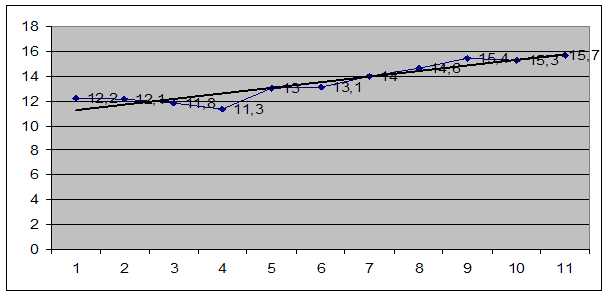
Рисунок 3.2 - Тенденция исходного временного ряда показателя уровня смертности

Тенденция исходного временного ряда описывается линейным уравнением тренда, что видно на рисунке 3.2.

Получили уравнение вида: ŷ_t = 10,844 + 0,443*t

Параметры уравнения вычислены с помощью метода наименьших квадратов.

Теперь определим начальные условия первого и второго порядков. Порядок начального условия определяется числом параметров линейного тренда.

Начальное условие первого порядка: S₀¹(y)=8,63;

начальное условие второго порядка: S₀²(y)= 6,42.

Следующим этапом является расчет экспоненциальных средних первого и второго порядков.

Экспоненциальная средняя первого порядка S_t¹(y)=13,04.

Экспоненциальная средняя второго порядка S_t²(y)= 7,52.

Прогноз строится по модели вида ŷ*_t+L = â₀ + â₁* t,

где t =1, â₀ = 18,56, â₁ = 1,1.

Сделаем прогноз на 2008 год, где t = 3, так как последний уровень ряда 2005 года.

ŷ*_3+L= 18,56 + 1,1*3;

ŷ*_3+L= 21,8.

Прогноз на 2009 год: ŷ*_4+L= 22,9.

По проделанным расчетам прогнозных данных можно сказать следующее, что рождаемость имеет тенденцию к возрастанию, в то же время и уровень смертности также имеет возрастающую тенденцию, показано на рисунке 3.3, 3.4. Это говорит о том, что численность населения республики будет все также сокращаться.

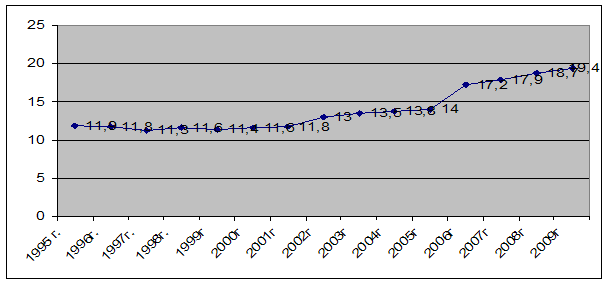
Рисунок 3.3 - прогноз уровня рождаемости

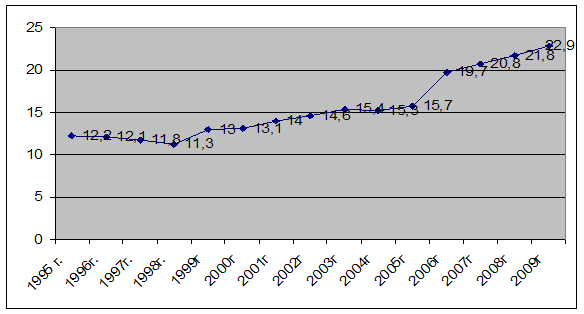
Рисунок 3.4 - Прогноз уровня смертности