Министерство образования РФ
КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра строительных конструкций
Курсовой проект
по дисциплине:
"Железобетонные и каменные конструкции"
КРАСНОДАР 2007
Содержание
1. Компоновка сборного ж. б. междуэтажного перекрытия
2. Проектирование предварительно напряжённой плиты перекрытия
2.1 Данные для расчёта
2.2 Расчётный пролёт и нагрузки
2.3 Усилия от расчётных и нормативных нагрузок
2.4 Компоновка поперечного сечения панели
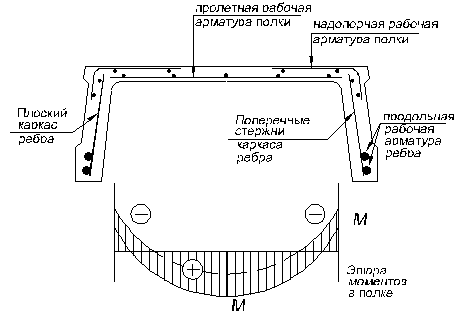
2.5 Расчёт полки на местный изгиб
2.6 Расчёт прочности сечений нормальных к оси панели
2.7 Расчёт прочности по наклонным сечениям
2.8 Расчёт преднапряжённой плиты по предельным состояниям второй группы
2.9 Расчёт панели на усилия, возникающие при изготовлении, транспортировании и монтаже
3. Расчёт неразрезного ж. б. ригеля
3.1 Статический расчёт неразрезного ж. б. ригеля
3.2 Расчёт ригеля по сечениям нормальным к продольной оси
3.3 Расчёт прочности ригеля по сечениям наклонным к продольной оси
3.4 Построение эпюры арматуры
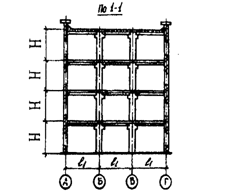
1. Компоновка сборного ж. б. междуэтажного перекрытия
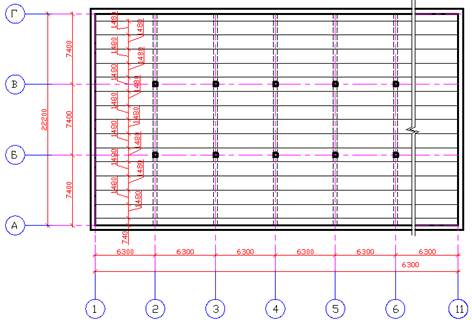
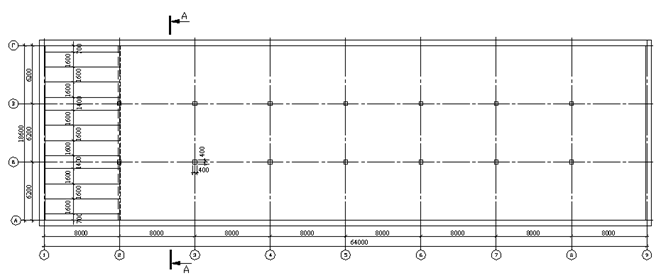
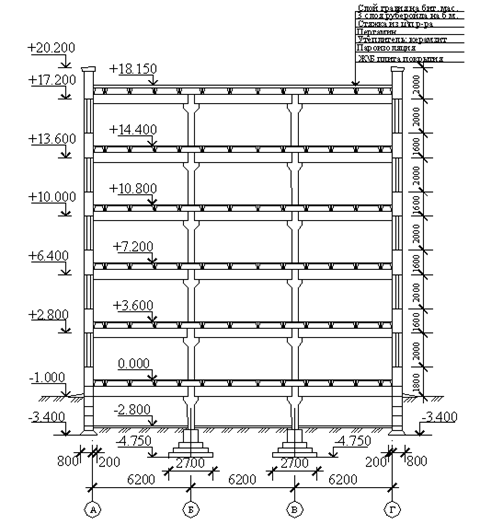
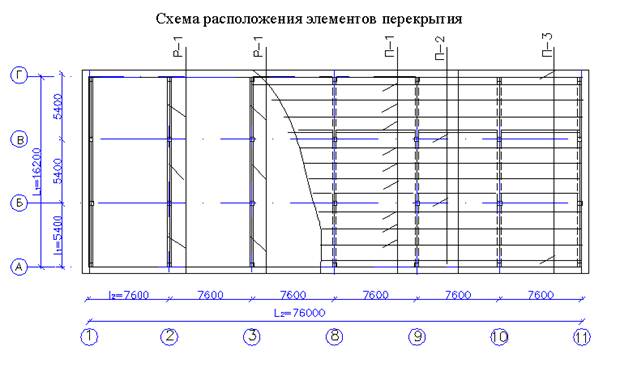
Рис.1. Схема компоновки сборного ж. б. перекрытия.
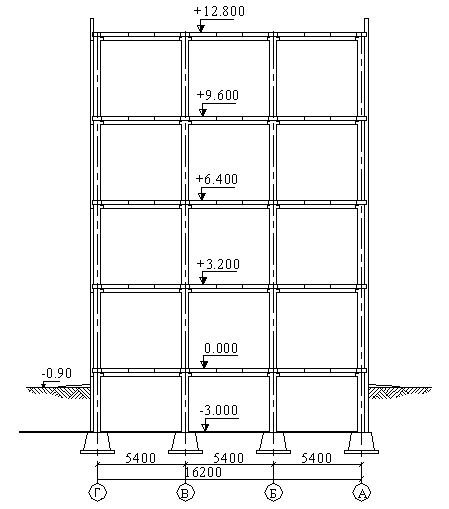
Размеры здания в осях: длина 63м., ширина22,2м. В продольном направлении проведено 4 оси т.е. получили 3 пролёта, в поперечном направлении проведено 11 осей т.е. получили 10 пролётов. Ригели укладываются в поперечном направлении. Размеры конструктивной ячейки 6.3![]() 7.4 м. Ребристые плиты опираем поверху и укладываем в продольном направлении. Схема сборного ж. б. перекрытия изображена на рисунке №1.
7.4 м. Ребристые плиты опираем поверху и укладываем в продольном направлении. Схема сборного ж. б. перекрытия изображена на рисунке №1.
2. Проектирование предварительно напряжённой плиты перекрытия
Сбор нагрузок на перекрытие.
Постоянные нагрузки, действующие на элементы перекрытий (покрытий) складываются из нагрузки от веса пола (кровли) и нагрузки от веса несущих ж. б. конструкций.
Нагрузки от веса ![]() конструкций пола (на плиту перекрытия) принимаем одинаковой на всех этажах.
конструкций пола (на плиту перекрытия) принимаем одинаковой на всех этажах.
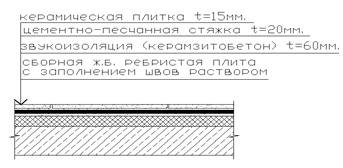
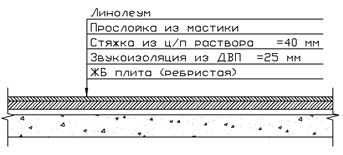
Рис.2. Элемент перекрытия.
Таблица 1.1 Нагрузка 1![]() междуэтажного перекрытия
междуэтажного перекрытия
| № п/п | Наименование нагрузки | Нормативная нагрузка, Па. | Коэф. надёж-ности по Нагрузке | Расчётная Нагрузка Па. |
| 1 | Постоянная: керамическая плитка t=15мм. цементно-песчаная стяжка t=20мм. звукоизоляция (керамзитобетон) t=60мм. Нагрузка от пола Сборная ж. б. ребристая плита с заполнением швов раствором ИТОГО: | 300 360 600 1260 2500 3760 | 1.1 1.2 1.2 1.1 | 330 430 720 1480 2750 4230 |
| 2 | Временная полезная нагрузка в том числе длительная кратковременная | 9000 7500 1500 | 1.2 1.2 | 10800 9000 1800 |
Высоту сечения предварительно напряжённых плит, предварительно назначаем равной
![]() .
.
Для дальнейшего расчёта принимаем ![]()
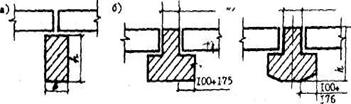
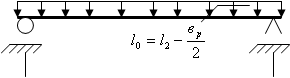
Расчётный пролёт при опирании плиты на ригель по верху:
![]()
где l - номинальный пролёт панели, м. Рис.2.2
![]() -ширина ригеля, м. К определению расчётного
-ширина ригеля, м. К определению расчётного
![]() пролёта панели
пролёта панели
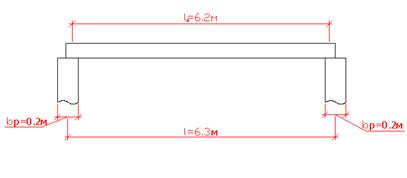
![]() Номинальная ширина плиты 1.48м. Материал для плиты: бетон класса В30, напрягаемая арматура класса А-lllв.
Номинальная ширина плиты 1.48м. Материал для плиты: бетон класса В30, напрягаемая арматура класса А-lllв.
![]() Призменная прочность нормативная
Призменная прочность нормативная ![]() ; расчётная
; расчётная ![]() ; коэффициент условий работы бетона
; коэффициент условий работы бетона![]() . Нормативное сопротивление при растяжении
. Нормативное сопротивление при растяжении ![]() , расчётное
, расчётное ![]() . Начальный модуль упругости бетона
. Начальный модуль упругости бетона ![]() .
.
![]() Арматура продольных рёбер класса Аlllв нормативное сопротивление
Арматура продольных рёбер класса Аlllв нормативное сопротивление ![]() , расчётное сопротивление
, расчётное сопротивление ![]() , модуль упругости
, модуль упругости ![]() .
.
![]() Ненапрягаемая арматура: в полке панели сварные сетки класса Аlll c
Ненапрягаемая арматура: в полке панели сварные сетки класса Аlll c ![]() ; в продольных и поперечных рёбрах сварные каркасы с продольной рабочей арматурой класса А1
; в продольных и поперечных рёбрах сварные каркасы с продольной рабочей арматурой класса А1 ![]() .
.
![]() Технология изготовления плиты -агрегатно-поточная с пропариванием.
Технология изготовления плиты -агрегатно-поточная с пропариванием.
![]() Рассчитываемая панель будет работать в закрытом помещении при влажности воздуха окружающей среды выше 40%.
Рассчитываемая панель будет работать в закрытом помещении при влажности воздуха окружающей среды выше 40%.
![]() Требования предельных состояний второй группы:
Требования предельных состояний второй группы:
![]() к трещиностойкости панели перекрытия предъявляется 3-я категория трещиностойкости: допускается ограничение по ширине непродолжительное
к трещиностойкости панели перекрытия предъявляется 3-я категория трещиностойкости: допускается ограничение по ширине непродолжительное ![]() и продолжительное
и продолжительное ![]() раскрытие трещин.
раскрытие трещин.
![]() Предельно допустимый прогиб панели
Предельно допустимый прогиб панели ![]() <l<10м) равен
<l<10м) равен ![]()
Расчётная нагрузка на 1 м длинны при ширине плиты 1.48м
постоянная: ![]()
полная: ![]()
Нормативная нагрузка на 1 м длинны.
постоянная: ![]()
полная: ![]()
в том числе постоянная и длительная полная: ![]()
От расчётной нагрузки:
![]()
![]()
От нормативной полной нагрузки:
![]()
![]()
От нормативной постоянной и длительной:
![]()
![]()
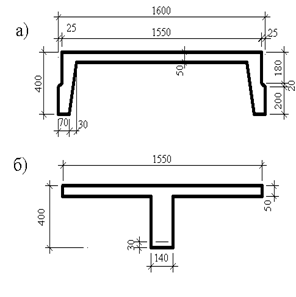
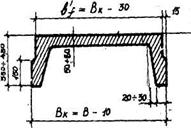
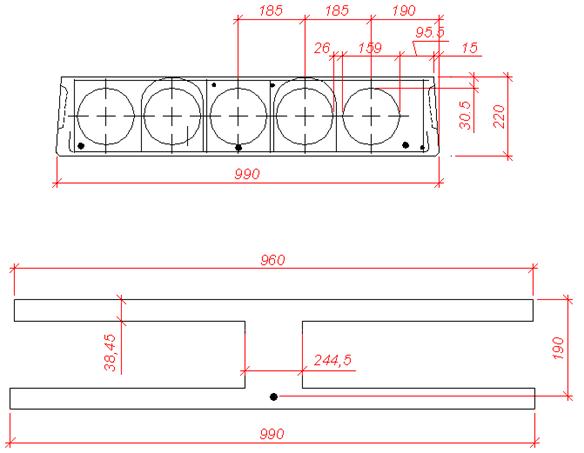
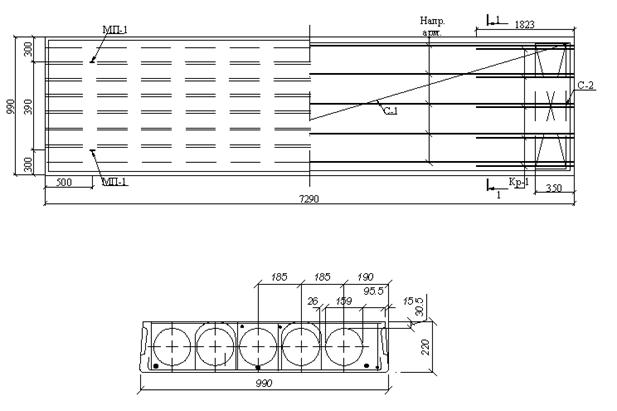
Принимаем панель со следующими параметрами (рис2.3): высота сечения предварительно-напряжённой плиты ![]() , принимаем
, принимаем ![]() ,
,
Рабочая высота сечения ![]() , ширина панели понизу
, ширина панели понизу ![]() , ширина панели по верху
, ширина панели по верху ![]() , толщина полки
, толщина полки ![]() , ширина продольных рёбер по низу -
, ширина продольных рёбер по низу -![]()
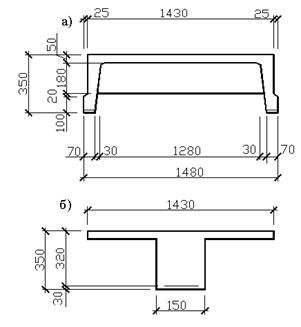
Рис 2.3 Ребристая панель: а) проектное сечение; б) приведённое сечение.
Приведённое поперечное сечение (рис.2.3б) имеет тавровую форму со следующими параметрами ![]() ,
, ![]() , при этом вводится вся (ребристая панель) ширина полки
, при этом вводится вся (ребристая панель) ширина полки ![]() , расчётная ширина ребра
, расчётная ширина ребра
![]() .
.
Расчётный пролёт при ширине рёбер вверху составит ![]() , где 8см - ширина продольного ребра вверху. Расчётная нагрузка на
, где 8см - ширина продольного ребра вверху. Расчётная нагрузка на ![]() полки:
полки:
![]() ,
,
где ![]() и
и ![]() принимаются по табл.1
принимаются по табл.1
![]() -
-
нагрузка от собственной массы полки.
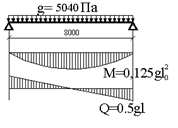
Изгибающий момент для полосы шириной 1м определяется с учётом пластичной заделки в рёбрах
![]()
Рабочая высота сечения
![]()
Арматура Аlll с
![]()
![]()
Из таблицы 3.1 (2) найдём
![]() ,
, ![]()
По приложению 6 (2) принимаем 7ø6 Аlll с шагом 180мм с ![]()
![]()
Сечение тавровое с полкой в сжатой зоне, вычисляем
![]()
Из таблицы 3.1 (2) найдём
![]()
![]() ;
; ![]()
Нейтральная ось проходит в пределах сжатой зоны
![]()
Вычисляем характеристики сжатой зоны
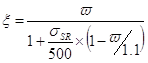 ;
;
![]() ;
;
![]() ,
,
![]() ,
,
Проверим, выполняется ли условие: ![]()
![]() ; где при электротермическом способе натяжения
; где при электротермическом способе натяжения ![]() , где l - длина элемента в пролётах.
, где l - длина элемента в пролётах.
![]() ;
;
![]() ;
;
![]() ;
;
условие выполняется
![]()
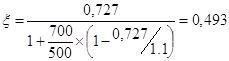 .
.
Вычисляем предельное отклонение предварительного напряжения:
D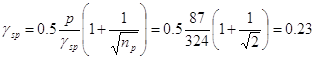 ,
,
где n=2 - число напрягаемых стержней плиты.
Коэффициент точности натяжения
![]() D
D![]()
Предварительное натяжение с учётом точности натяжения:
![]() ,
,
Предварительное напряжение с учётом полных потерь предварительно принято равным ![]() .
.
При расчёте на прочность железобетонных элементов с высокопрочной арматурой классов: А4, А5, А6, В2, К7и К19 при соблюдении условия![]() , расчётное сопротивление арматуры
, расчётное сопротивление арматуры ![]() должно быть умножено на коэффициент
должно быть умножено на коэффициент![]()
![]() ;
;
![]() ,
,
![]() -коэффициент, принимаемый равный для класса арматуры Аlllв 1,2
-коэффициент, принимаемый равный для класса арматуры Аlllв 1,2
![]()
Применяем для арматуры класса Аlllв
![]()
![]()
По приложению 6 (2) принимаем 2ø20 Аlllв с ![]()
Вычисляем проекцию расчётного наклонного сечения на продольную ось ”С” по формуле:
![]() ,
,
где ![]() для тяжёлого бетона коэффициент, учитывающий влияние вида бетона
для тяжёлого бетона коэффициент, учитывающий влияние вида бетона
![]() - коэффициент, учитывающий влияние продольных сил.
- коэффициент, учитывающий влияние продольных сил.
![]() ; где
; где
![]() -
-
усилие предварительного обжатия, после проявления всех потерь принято равным 0,7 от начального натяжения.
![]()
![]() -коэффициент, учитывающий сжатых полок в тавровых и двутавровых элементах, определяется по формуле
-коэффициент, учитывающий сжатых полок в тавровых и двутавровых элементах, определяется по формуле
![]()
![]() , суммарное значение
, суммарное значение ![]()
Принимаем ![]() .
.
В расчётном наклонном сечении:
![]()
![]()
принимаем ![]() , тогда
, тогда
![]() ,
,
следовательно поперечная арматура по расчёту не требуется.
На приопорных участках длинной ![]() устанавливаем конструктивную арматуру
устанавливаем конструктивную арматуру
ø6 Аlll с шагом![]() . В средней части пролёта
. В средней части пролёта ![]() .
.
Геометрические характеристики приведённого сечения (рисунок 2.3)
Отношение модулей упругости
![]()
Площадь приведённого сечения
![]()
Статический момент площади приведённого сечения относительно нижней грани
![]()
![]()
Момент инерции приведённого сечения
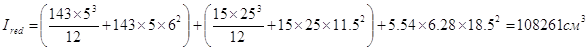
Момент сопротивления приведённого сечения по нижней зоне
![]()
Момент сопротивления приведённого сечения по верхней зоне
![]()
Расстояние от ядровой точки, наиболее удаленной от растянутой зоны (верхней) до центра тяжести приведённого сечения
![]()
Где
![]()
![]() ,
,
отношение ![]() предварительно принимаем 0,75 согласно таблице 2.4 (2)
предварительно принимаем 0,75 согласно таблице 2.4 (2)
Упругопластический момент сопротивления по растянутой зоне.
![]() ,
,
![]() - коэффициент, принимаемый для тавровых сечений с полкой в сжатой зоне.
- коэффициент, принимаемый для тавровых сечений с полкой в сжатой зоне.
Упругопластический момент по растянутой зоне в стадии изготовления и обжатия элемента
![]()
где ![]() - коэффициент, принимаемый для таврового сечения с полкой в растянутой зоне при
- коэффициент, принимаемый для таврового сечения с полкой в растянутой зоне при
![]() и
и ![]()
Потери предварительного напряжения арматуры: потери от релаксации напряжений в арматуре при электротермическом способе натяжения
![]()
потери от температурного перепада, между натянутой арматурой и упорами ![]() так как при пропаривании форма с упорами нагревается вместе с изделием. Усилие обжатия с учётом полных потерь
так как при пропаривании форма с упорами нагревается вместе с изделием. Усилие обжатия с учётом полных потерь
![]()
Эксцентриситет этого усилия относительно центра тяжести приведённого сечения
![]()
Напряжение в бетоне при обжатии:
![]()
Устанавливаем величину придаточной прочности бетона из условия:
![]() принимаем
принимаем ![]() ,
,
вычисляем сжимающие напряжения в бетоне на уровне центра тяжести напрягаемой арматуры от усилия обжатия ![]() с учётом изгибающего момента от массы.
с учётом изгибающего момента от массы.
![]() , тогда
, тогда
![]()
Потери от быстронатекающей ползучести
![]() , где
, где
![]()
![]() ,
,
принимаем ![]() , тогда
, тогда
![]() ;
; ![]() : потери от усадки бетона
: потери от усадки бетона ![]() , потери от ползучести бетона при
, потери от ползучести бетона при ![]() ,
, ![]() .
.
Вторичные потери
![]() ,
,
полные потери
![]() ,
, ![]()
т.е. больше установленного минимального значения потерь.
Усилие обжатия с учётом полных потерь:
![]()
Расчёт по образованию трещин, нормальных к продольной оси.
![]()
Вычисляем момент образования трещин по приближённому способу ядровых моментов
![]()
Здесь ядровый момент усилия обжатия при
![]() ,
, ![]()
Поскольку ![]() , трещины в растянутой зоне образуются, следовательно необходим расчёт по раскрытию трещин.
, трещины в растянутой зоне образуются, следовательно необходим расчёт по раскрытию трещин.
Проверим, образуются ли начальные трещины в верхней зоне плиты при её обжатии при значении коэффициента точности натяжения ![]() изгибающий момент от собственной массы плиты
изгибающий момент от собственной массы плиты ![]() .
.
Расчётное условие:
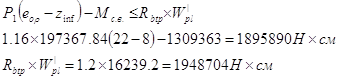
![]() -
-
условие удовлетворяется, начальные трещины не образуются: здесь ![]() - сопротивление бетона растяжению соответствующий передаточной прочности бетона
- сопротивление бетона растяжению соответствующий передаточной прочности бетона ![]() .
.
Расчёт по раскрытию трещин, нормальных к продольной оси.
Изгибающий момент от нормативных нагрузок:
постоянной и длительной ![]()
полной ![]() .
.
Приращение напряжений в растянутой арматуре от действия постоянной и длительной нагрузок:
![]() ,
,
Где ![]() - плечо внутренней пары сил;
- плечо внутренней пары сил; ![]() т.к Р - усилие обжатия приложено в центре тяжести площади нижней напрягаемой арматуры.
т.к Р - усилие обжатия приложено в центре тяжести площади нижней напрягаемой арматуры.
![]()
- момент сопротивления сечения по растянутой арматуре.
Приращение напряжений в арматуре от действия полной нагрузки:
![]()
Ширина раскрытия трещин от непродолжительного действия всей нагрузки
![]()
![]()
![]() - диаметр продольной арматуры.
- диаметр продольной арматуры.
Ширина раскрытия трещин от непродолжительного действия постоянной и длительной нагрузок.
![]()
Ширина раскрытия трещин от постоянной и длительной нагрузок
![]()
Непродолжительная ширина раскрытия трещин
![]()
Продолжительная ширина раскрытия трещин
![]()
Расчёт плиты по деформациям (определение прогиба).
Заменяющий момент равен изгибающему моменту от постоянной и длительной нагрузки ![]() , суммарная продольная сила равна усилию предварительного обжатия с учётом всех потерь при
, суммарная продольная сила равна усилию предварительного обжатия с учётом всех потерь при ![]() .
.
![]() , эксцентриситет
, эксцентриситет ![]()
Коэффициент ![]() при длительном действии нагрузки
при длительном действии нагрузки
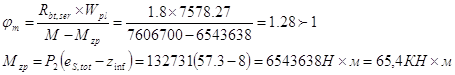
Принимаем ![]() .
.
Определяем коэффициент ![]() , характеризующий неравномерность деформаций растянутой арматуры на участках между трещинами.
, характеризующий неравномерность деформаций растянутой арматуры на участках между трещинами.
![]()
Вычисляем кривизну оси при изгибе:
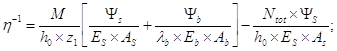
где
![]()
![]()
![]()
![]()
Вычисляем прогиб:
![]()
За расчётное сечение принимаем сечение, расположенное на расстоянии 0,8м от торца панели.
Расчет ведём на совместное действие внецентренного сжатия ![]() и изгибающего момента от собственной массы.
и изгибающего момента от собственной массы.
![]()
тогда
![]()
Определяем
![]() ,
,
По таблице 3,1 (2) находим ![]() , тогда
, тогда ![]()
![]()
Следовательно в верхней зоне должно быть не менее 2ø16 класса Аlll с ![]()
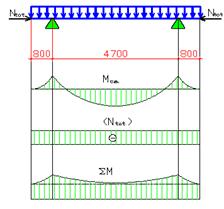
Рисунок 2.4 - К расчёту панели в стадии изготовления, транспортирования и монтажа.
3. Расчёт неразрезного ж. б. ригеля 3.1 Статический расчёт неразрезного ж. б. ригеля
Определяем расчётные пролёты:
крайний пролёт:
![]()
средний пролёт: ![]()
Определяем размеры ригеля:
![]() ,
, ![]()
Нагрузка от массы ригеля:
![]()
Нагрузки собираем на ригель с грузовой полосы линейно равной номинальной длине плит перекрытия.
постоянная на перекрытие с учётом коэффициента надёжности по назначению здания
![]() ,
, ![]()
от массы ригеля с учётом коэффициента надёжности ![]() и
и ![]()
![]()
Итого
![]()
Временная нагрузка с учётом коэффициента надёжности по назначению здания![]() :
:
![]() ;
;
q=![]()
Статический расчёт ригеля на вертикальную нагрузку производится в составе поперечной рамы так как сосредоточенных нагрузок по пять в каждом пролёте то заменяем их эквивалентной равномернораспределённой нагрузкой.
![]() Нагрузки на ригель передаются через рёбра ребристых плит и составит:
Нагрузки на ригель передаются через рёбра ребристых плит и составит:
![]() и
и ![]()
В среднем:
![]()
![]()
![]()
Для временной расчётной
![]() и
и ![]()
В среднем:
![]()
![]()
Жёсткостные параметры рамы:
![]()
![]()
![]()
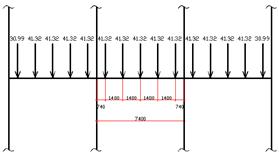
![]() Рисунок 3,1 - Схема расположения сосредоточенных нагрузок.
Рисунок 3,1 - Схема расположения сосредоточенных нагрузок.
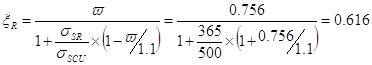
![]()
![]()
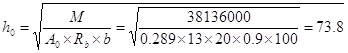
Полная высота сечения ![]() принимаем
принимаем ![]()
![]() . Для опорных и в пролётах сечениях принято расстояние от границы растянутой зоны до центра тяжести арматуры а=6см.
. Для опорных и в пролётах сечениях принято расстояние от границы растянутой зоны до центра тяжести арматуры а=6см.
Сечение в первом пролёте ![]() и
и ![]()
![]()
по таблице 3,1 (2) ![]()
![]() .
.
Проверяем принятую высоту сечения ригеля по наибольшему моменту.
Поскольку ![]() сечение не будет переармированным.
сечение не будет переармированным.
Определяем площадь поперечного сечения продольной арматуры:
![]()
По сортаменту (приложение 6 (2)), принимаем 4ø28 класса Аlll с ![]()
Сечение в среднем пролёте ![]()
![]()
по таблице 3,1 (2) ![]() .
.
![]()
По сортаменту (приложение 6 (2)), принимаем 4ø20 класса Аlll с ![]() . Количество верхней арматуры определяем по величине опорных изгибающих моментов. На опоре <Б>.
. Количество верхней арматуры определяем по величине опорных изгибающих моментов. На опоре <Б>.
![]()
по таблице 3,1 (2) ![]() .
.
![]()
Для армирования опорных сечений справа и слева принимаем 4ø25 класса Аlll с ![]() .
.
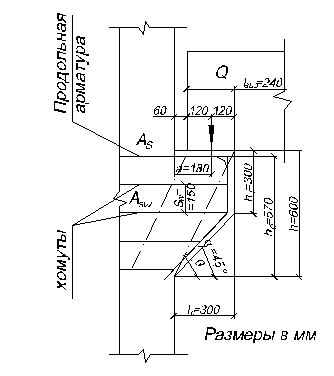
На крайней опоре поперечная сила ![]() , вычисляем проекцию расчётного наклонного сечения на ось по формулам гл.3 (2)
, вычисляем проекцию расчётного наклонного сечения на ось по формулам гл.3 (2)
![]()
В расчётном наклонном сечении:
![]() , отсюда
, отсюда ![]() ,
,
принимаем ![]() , тогда
, тогда
![]() ,
,
следовательно необходима поперечная арматура, вычисляем:
![]()
![]()
Диаметр поперечных стержней устанавливаем из условия сварки с продольной арматурой ø=28мм по приложению 9 (2) ![]() класса Аlll с
класса Аlll с ![]() .
.
Число каркасов 2 при этом ![]() . Определяем шаг
. Определяем шаг ![]() , на приопорных участках длинной
, на приопорных участках длинной ![]() , в средней части пролёта
, в средней части пролёта![]() .
.
Проверяем прочность по сжатой полосе между наклонными трещинами:
![]() ,
,
![]()
![]()
![]()
Условие
![]() удовлетворяется!
удовлетворяется!
Очевидно, что условие будет удовлетворятся и для наклонных сечений у опоры <Б>, поэтому расчёт в дальнейшем не повторяем. На первой промежуточной опоре слева поперечная сила ![]() из предыдущего расчёта принимаем
из предыдущего расчёта принимаем ![]() , тогда в расчётном приопорном сечении:
, тогда в расчётном приопорном сечении:
![]() ,
,
отсюда
![]() ,
,
Вычисляем:
![]()
![]()
Определяем шаг поперечных стержней
![]() .
.
Принимаем на приопорном участке длинной ![]() , слева от опоры
, слева от опоры ![]() . На первой промежуточной опоре слева:
. На первой промежуточной опоре слева:
![]()
![]() ,
,
Вычисляем:
![]()
![]()
Определяем шаг поперечных стержней
![]() .
.
Принимаем на приопорном участке справа ![]() , в средней части второго пролёта принимаем
, в средней части второго пролёта принимаем ![]() .
.
Сечение в первом пролёте 4ø28 класса Аlll с ![]() , определяем момент, воспринимаемый сечением, для чего рассчитываем необходимые параметры:
, определяем момент, воспринимаемый сечением, для чего рассчитываем необходимые параметры:
![]()
![]()
![]() ,
, ![]()
![]()
Арматура 2ø28 класса Аlll с ![]() доводится до опор а стержни 2ø28 обрываются в пролёте. Определяем момент, воспринимаемый сечением с арматурой 2ø28 Аlll.
доводится до опор а стержни 2ø28 обрываются в пролёте. Определяем момент, воспринимаемый сечением с арматурой 2ø28 Аlll.
![]()
![]()
![]() ,
, ![]()
![]()
Графически определяем точки обрыва двух стержней ø28. В первом сечении поперечная сила ![]() , во втором
, во втором ![]() . Интенсивность поперечного армирования в первом сечении при шаге хомутов
. Интенсивность поперечного армирования в первом сечении при шаге хомутов ![]() равна:
равна:
![]() ,
,
![]()
Во втором сечении при шаге хомутов ![]()
![]()
![]()
На первой промежуточной опоре слева и справа принята арматура 2ø25+2ø25 с ![]() .
.
![]()
![]()
![]() ,
, ![]()
![]()
Вместе теоретического обрыва остаются 2ø25 с ![]() . Определяем момент, воспринимаемый сечением с этой арматурой.
. Определяем момент, воспринимаемый сечением с этой арматурой.
![]()
![]()
![]() ,
, ![]()
![]()
Графически определяем точки обрыва двух стержней ø25.
поперечная сила, ![]() . Интенсивность поперечного армирования в первом сечении при шаге хомутов
. Интенсивность поперечного армирования в первом сечении при шаге хомутов ![]() равна:
равна:
![]()
![]()
Расчёт эпюры арматуры для второго пролёта.
Сечение во втором пролёте 4ø20 класса Аlll с ![]() , определяем момент, воспринимаемый сечением, для чего рассчитываем необходимые параметры:
, определяем момент, воспринимаемый сечением, для чего рассчитываем необходимые параметры:
![]()
![]()
![]() ,
, ![]()
![]()
Арматура 2ø20 класса Аlll с ![]() доводится до опор а стержни 2ø28 обрываются в пролёте. Определяем момент, воспринимаемый сечением с арматурой 2ø20 Аlll
доводится до опор а стержни 2ø28 обрываются в пролёте. Определяем момент, воспринимаемый сечением с арматурой 2ø20 Аlll
![]()
![]()
![]() ,
, ![]()
![]()
Графически определяем точки обрыва двух стержней ø20
поперечная сила, ![]() . Интенсивность поперечного армирования в первом сечении при шаге хомутов
. Интенсивность поперечного армирования в первом сечении при шаге хомутов ![]() равна:
равна:
![]()
![]()
На первой промежуточной опоре справа принята та же арматура что и слева, следовательно момент от 4ø25 ![]()
момент от 2ø25 ![]()
Графически определяем точки обрыва двух стержней ø25. поперечная сила, ![]() . Интенсивность поперечного армирования в первом сечении при шаге хомутов
. Интенсивность поперечного армирования в первом сечении при шаге хомутов ![]() равна:
равна:
![]()
![]()
Похожие работы
... рабочей арматурой 18Æ10 АI с шагом s=13,5 см. см2. Процент армирования расчётного сечения 6. Расчёт и конструирование монолитного перекрытия 6.1. Компоновка ребристого монолитного перекрытия Проектируем монолитное ребристое перекрытие с продольными главными балками и поперечными второстепенными балками. При этом пролёт между осями рёбер равен (второстепенные балки ...
... стержней слева 2Ø28 А300: 504 мм < 20d = 560 мм справа 2Æ36 A-II (А300) 629 мм < 20d = 720 мм Принято W1= 500 мм; W2 = 550 мм; W3 = 600 мм; W4 = 750 мм. 6. Расчет сборной железобетонной колонны Сетка колонн м Высота этажей между отметками чистого пола – 3.3 м. Нормативное значение временной нагрузки на междуэтажные перекрытия 8.5 кH/м2, расчетное значение ...
... свариваемости назначается диаметр поперечной арматуры dsw. 2. По диаметру и количеству поперечных стержней в сечении определяется площадь поперечной арматуры. мм, Asw = n∙fsw, где n – количество каркасов в плите; fsw – площадь одного поперечного стержня. Asw = 1,01 см2, 3. По конструктивным условиям назначается шаг поперечных стержней S: - если высота плиты h ≤ 450 мм., ...
... на 1 м длины ригеля определяется с грузовой полосы, равной шагу рам, в данном случае шаг рам 5.4 м. Постоянная нагрузка : -от перекрытия с учетом коэффициента надежности по назначению здания ; -от веса ригеля , где 2500 кг/м3 – плотность железобетона. С учетом коэффициентов надежности по нагрузке и по назначению здания : кН/м. Итого: кН/м. Временная нагрузка с учетом коэффициента ...
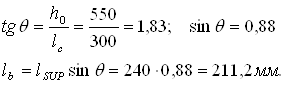

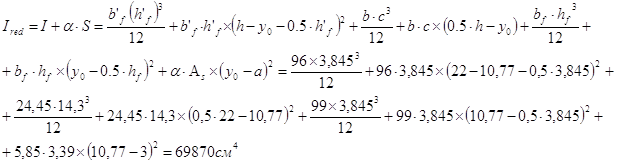
0 комментариев