Сети с переключением режимов при определенном количестве заявок в узле

1. Сети с переключением режимов при определенном количестве заявок в узле

Рассматриваются замкнутые сети массового обслуживания с экспоненциальным обслуживанием в узлах и марковской маршрутизацией. Однолинейные узлы могут работать в нескольких режимах, время переключения с одного режима на другой имеет показательное распределение. Переключение происходит только на соседние режимы и с определенными ограничениями на переключения в отдельных режимах. Устанавливается достаточное условие мультипликативности стационарного распределения состояний сети.

Пусть , где . На фазовом пространстве  задан многомерный марковский процесс , где , своими инфинитезимальными интенсивностями перехода

Интенсивности перехода из состояния  во все состояния, отличные от вышеперечисленных, предполагаются равными нулю. Здесь  при  и  при  и .

Марковский процесс  описывает замкнутую сеть, в которой циркулирует  заявок. В -м узле находится единственный экспоненциальный прибор с интенсивностью обслуживания , зависящей от состояния узла. Заявка, обслуженная в -м узле, переходит с вероятностью  в -й узел. Как и в случае открытых сетей компонента  выражает число заявок в -м узле, а компонента  – номер режима работы прибора. Прибор -го узла может работать в  режимах  с показательно распределенным временем пребывания в них;  – интенсивность увеличения номера режима на единицу,  – интенсивность уменьшения номера режима на единицу.

Глобальные уравнения равновесия для стационарных вероятностей этого марковского процесса имеют следующую форму:

Рассмотрим общий случай, когда для каждого узла  существует натуральное число  и конечное множество индексов  такое, что  для всех , у которых  для некоторого  и  для всех  иного вида.

Будем предполагать, что матрица  неприводима. Тогда уравнение трафика

имеет единственное с точностью до постоянного множителя положительное решение . Рассмотрим марковский процесс  на фазовом пространстве , заданный инфинитезимальными интенсивностями

для всех иных состояний  считаем, что . Процесс  описывает изолированный узел в фиктивной окружающей среде, в которой на узел посылается стационарный пуассоновский поток с параметром , где  – любое решение уравнения трафика (3.1.1). При этом узел предполагается имеющим ограниченную емкость . Это значит, что когда в нем находится  заявок и поступает заявка, то она теряется. Уравнения равновесия для стационарных вероятностей марковского процесса, описывающего такой узел, имеют следующий вид:

для

для

для  и для

для

Мы свяжем стационарное распределение  процесса  со стационарными распределениями  процессов  и будем интересоваться достаточными условиями выполнения равенства

где  – нормирующая постоянная, зависящая от числа узлов в сети и от числа циркулирующих в ней заявок.

В отличие от открытой сети, здесь удобнее пользоваться введенной в [36,37,42] концепцией ограниченной квазиобратимости. Как там показано, для замкнутых сетей ограниченная квазиобратимость дает более широкие достаточные условия для выполнения (3.1.9), чем квазиобратимость.

Лемма 1.1 [46, C.325]. Если для изолированного узла в фиктивной окружающей среде входящий поток является простейшим, то обратимость и ограниченная квазиобратимость эквивалентны.

Д о к а з а т.е. л ь с т в о. Для изолированного узла условие ограниченной -квазиобратимости из [36,37,42] принимает вид

а условие обратимости – форму

и для

Достаточно показать, что при выполнении (3.1.2) – (3.1.8) из (3.1.10) следует (3.1.11). Пусть  при некотором фиксированном . Докажем, что тогда для всех  выполняется (3.1.11). При  соотношение (3.1.11) следует из (3.1.4) и соотношения (3.1.10) для состояний  и . Предположим, что (3.1.11) выполняется для некоторого , т.е.

Тогда из (3.1.5) с учетом (3.1.12) и (3.1.10) для состояний  и  вытекает (3.1.11). Итак, (3.1.11) доказано с помощью индукции по . Лемма доказана.

Лемма 1.2 [46, C.325]. Для ограниченной -квазиобратимости изолированного -го узла необходимо и достаточно выполнения условий

а) для  при некотором

б) для всех

 

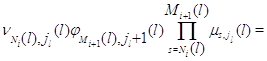
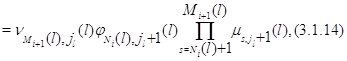
где при  не определенная ранее величина  должна быть заменена на . Марковский процесс  эргодичен, а его финальное стационарное распределение с точностью до постоянной нормировки  определяется соотношениями

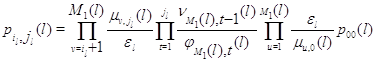
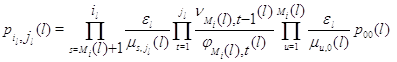
где при  последнее неравенство надо заменить на .

Д о к а з а т.е. л ь с т в о. Рассмотрим случайное блуждание по точкам с целочисленными координатами прямоугольника , задаваемое уравнениями (3.1.2) – (3.1.8). Равенство (3.1.13) есть циклическое условие Колмогорова (2.2.18) для четырехзвенных путей, проходящих через вершины элементарного квадрата  и идущих из  в  по и против часовой стрелки. Равенство (3.1.14) есть условие Колмогорова для -звенных путей, проходящих через вершины прямоугольника  и ведущих из  в  по и против часовой стрелки. Это доказывает необходимость условий (3.1.13) и (3.1.14) для обратимости, а значит (по лемме 3.1) ограниченной -квазиобратимости изолированного узла в фиктивной окружающей среде. Предположим, что (3.1.13), (3.1.14) выполнены. Любой замкнутый путь из  в  без самопересечений либо а) представляет собой некоторую однозвенную замкнутую дугу, либо б) проходит по границе некоторой фигуры, составленной из конечного числа примыкающих друг к другу элементарных квадратов и определенных выше - звенных прямоугольников. Для случая а) циклическое условие (2.2.18) выполняется автоматически. В случае б) перемножим равенства (3.1.13) для всех элементарных квадратов и равенства (3.1.14) для всех прямоугольников, из которых состоит упомянутая фигура. При этом интенсивности перехода для тех направленных дуг, которые не принадлежат границе фигуры, войдут множителями как в левую, так и в правую части. После сокращения на них получится циклическое условие (2.2.18) для путей, идущих по границе фигуры по и против часовой стрелки. Достаточность условий (3.1.13) и (3.1.14) доказана.

Докажем, что стационарное распределение изолированного узла в фиктивной окружающей среде имеет форму (3.1.15), (3.1.16). Полагая в (3.1.11)  получим:

откуда получаем

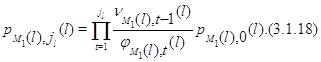
Из (3.1.10) для  находим, что

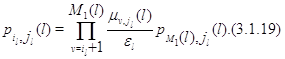
Для таких же  из (3.1.10) также следует, что

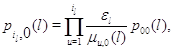
в частности,

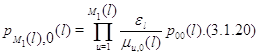
Подставляя (3.1.20) в (3.1.18), а затем подставляя полученное равенство в (3.1.19), будем иметь для

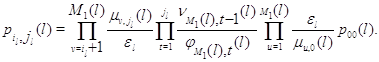
Тем самым доказано (3.1.15).

Для  из (3.1.10) следует, что

Полагая в (3.1.11) , получим:

откуда

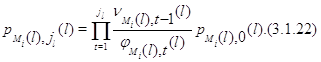
Далее, из (3.1.10)

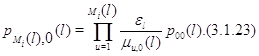
Подставляя (3.1.23) в (3.1.22), а затем полученное равенство в (3.1.21), для  будем иметь

Таким образом, (3.1.16) доказано для

Для  из (3.1.10) следует, что

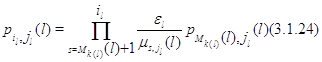
Полагая в (3.1.11) , получим:

откуда

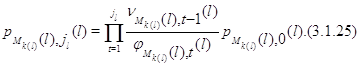
Далее, из (3.1.10)

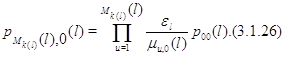
Подставляя (3.1.26) в (3.1.25), а затем полученное равенство в (3.1.24), получим (3.1.16), которое таким образом доказано и для .

Так как  – неприводимый процесс Маркова с конечным числом состояний и непрерывным временем, то по эргодической теореме Маркова [5] он является эргодическим. Лемма 3.2 полностью доказана.

Основной результат 3.1 заключается в следующем.

Теорема 1.1. [46, C.326], [53, C.159–160], [56, C.325–326] Марковский процесс  эргодичен. Для того, чтобы его стационарное распределение представлялось в форме произведения (3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия (3.1.13), (3.1.14). При этом множители в (3.1.9) имеют форму (3.1.15), (3.1.16), в которых полагается, что , а постоянная  имеет вид:

 

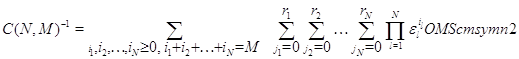
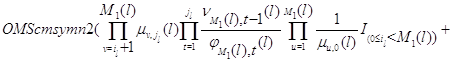
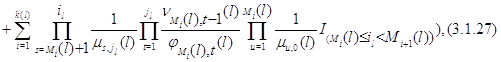
где .

Д о к а з а т.е. л ь с т в о. Так как марковский процесс с непрерывным временем и конечным числом состояний является неприводимым, то он эргодичен по эргодической теореме Маркова [5]. В [42] для замкнутых сетей с «заявкосохраняющими»  узлами установлено, что для мультипликативности стационарного распределения достаточно, чтобы нетерминальные узлы являлись ограниченно -квазиобратимыми. Поэтому, с учетом условия ограниченной -квазиобратимости для изолированного узла, которое в силу леммы 3.2 для узла с номером  принимает форму (3.1.13), (3.1.14), имеет место первое утверждение теоремы.

Наконец, поскольку сумма всех стационарных вероятностей должна быть равна единице, то подставляя в равенство

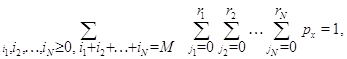
вместо  произведение (3.1.9) и учитывая (3.1.15), (3.1.16), после очевидных преобразований получим

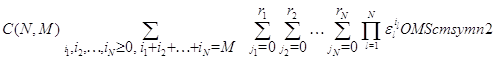
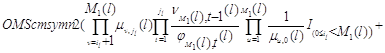
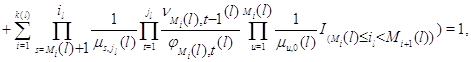
откуда вытекает (3.1.27). Теорема доказана.

Замечание 3.1. Если условия (3.1.13), (3.1.14) выполнены во всех узлах, то получается следующий алгоритм для нахождения стационарных вероятностей:

1. Решается система линейных уравнений (3.1.1). В качестве используемого в дальнейшем набора  берется любой набор со строго положительными координатами.