Проверяется выполнение условий (3.1.13), (3.1.14)

2. Проверяется выполнение условий (3.1.13), (3.1.14).

3. По формуле (3.1.27) определяется постоянная нормировки .

4. Определяются  с помощью соотношений (3.1.15), (3.1.16).

5. Находится стационарное распределение состояний сети  с помощью формулы (3.1.9).

Отметим также, что если в сети есть узлы, в которых условия (3.1.13), (3.1.14) не выполняются, то алгоритм существенно усложнится, так как в этих узлах нельзя применить (3.1.15), (3.1.16). Поэтому для таких узлов необходимо добавить процедуру численного решения системы уравнений (3.1.2) – (3.1.8). При этом изменится также выражение для подсчета нормирующей постоянной . Известно, что наиболее трудоемким этапом при вычислении стационарного распределения для замкнутых сетей является этап подсчета нормирующей постоянной. Существуют различные численные процедуры, разработанные для ее вычисления, например, анализ средних значений [10], или алгоритм, рекуррентный по времени [4,10].

2. Примеры замкнутых сетей с переключением режимов

В 3.1 рассматривалась весьма общая модель замкнутой сети с многорежимными стратегиями. Здесь мы рассмотрим несколько полезных для различных приложений частных случаев этой модели. Во всех рассматриваемых ниже примерах предполагается, что для  выполняется  при  и  при .

Случай . Пусть для всех  выполняется  для  и  для , а также  для  и  для . Это соответствует тому, что в модели из 3.1 полагается . Теорема 3.1 принимает следующий вид.

Следствие 2.1. Марковский процесс  эргодичен. Для того, чтобы его стационарное распределение представлялось в мультипликативной форме (3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия

Множители в (3.1.9) имеют форму

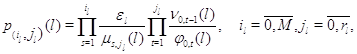
а постоянная нормировки имеет вид

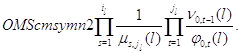
Случай . Во многих практических ситуациях переход с одного режима работы на другие невозможен, когда в узле нет заявок. Поэтому пусть для всех  выполняется  при . Пусть также для всех  выполняется  для  и  для , а также  для  и  для . Это соответствует тому, что в модели из 3.1 полагается .

Следствие 2.2. Марковский процесс  эргодичен. Для того, чтобы его стационарное распределение представлялось в мультипликативной форме (3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия

Множители в (3.1.9) имеют форму

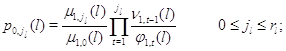
а постоянная нормировки имеет вид

Случай . Предположим, что когда все  заявок скапливаются в одном узле, прибор не может переходить с одного режима работы на другие:  при . Пусть также для всех  выполняется  для  и  для , а также  для  и  для . Это соответствует тому, что в модели из 3.1 полагается .

Следствие 2.3. Марковский процесс  эргодичен. Для того, чтобы его стационарное распределение представлялось в мультипликативной форме (3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия

Множители в (3.1.9) имеют форму

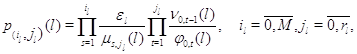
а постоянная нормировки имеет вид

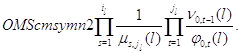
Случай . Когда в узле нет заявок или все заявки скапливаются в нем, переход с одного режима работы на другие невозможен:  при  или . Пусть также для всех  выполняется  для  и  для , а также  для  и  для . Это соответствует тому, что в модели из 3.1 полагается .

Следствие 2.4. Марковский процесс  эргодичен. Для того, чтобы его стационарное распределение представлялось в мультипликативной форме (3.1.9), достаточно, чтобы во всех узлах сети выполнялись условия

Множители в (3.1.9) имеют форму

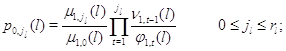
а постоянная нормировки имеет вид

В следующих двух случаях стационарное распределение всегда имеет форму произведения, поскольку марковский процесс, описывающий изолированный узел в фиктивной окружающей среде, обратим. Поэтому не надо накладывать никаких ограничений типа (3.1.13), (3.1.14).

Случай . Прибор может переключаться с одного режима работы на другие только тогда, когда в узле нет заявок: для  выполняется  при  и  при . Кроме того для всех  выполняется . Это соответствует тому, что в модели из 3.1 полагается .

Следствие 2.5. Марковский процесс  эргодичен, а его стационарное распределение представляется в мультипликативной форме (3.1.9), множители в которой имеют форму

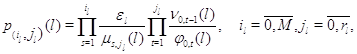
а постоянная нормировки имеет вид

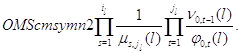
Случай . Переход с одного режима работы прибора на другие возможен только тогда, когда все заявки скапливаются в узле: для  выполняется  при  и  при . Кроме того для всех  выполняется . Это соответствует тому, что в модели из 3.1 полагается .

Следствие 2.6. Марковский процесс  эргодичен, а его стационарное распределение представляется в мультипликативной форме (3.1.9), множители в которой имеют форму

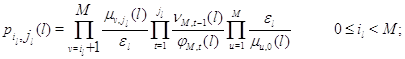
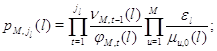
Можно выписать решения для других интересных с практической точки зрения случаев. Например, можно рассмотреть случай, когда переключение с одного режима работы на другой может производиться только при определенном фиксированном числе заявок в -ом узле , где . В этом случае марковский процесс  обратим без всяких дополнительных предположений типа (3.1.13), (3.1.14).

Заключение

В работе рассмотрена задача установления достаточных условий, которые надо наложить на изолированные узлы замкнутой сети массового обслуживания с многорежимными стратегиями обслуживания, чтобы стационарное распределение состояний сети имело мультипликативную форму с множителями, зависящими от состояний отдельных узлов. При этом изолированные узлы помещаются в фиктивную окружающую среду, характеризующуюся поступлением в них пуассоновских потоков заявок. Такие достаточные условия мультипликативности стационарного распределения состояний замкнутой сети в стационарном режиме ее работы установлены как для случая, когда интенсивности перехода в соседние режимы работы строго положительны при любых числах заявок в узлах, так и для случая, когда при определенных числах заявок в узлах они строго положительны, а при других числах все они равны нулю.

Доказана эргодичность марковского процесса, описывающего состояния сети. При выполнении установленных достаточных условий мультипликативности в аналитической форме найдены множители в мультипликативном представлении стационарного распределения и нормирующая постоянная. Построен алгоритм для расчета стационарных вероятностей состояний сети.

Литература

1. Кениг Д., Рыков В.В., Шмидт Ф. Стационарные системы массового обслуживания с зависимостями // Итоги науки и техники. – М., 1981. – Т.18. – С. 95–186. – (Сер. Теория вероятностей. Матем. статистика. Теор. кибернетика / ВИНИТИ).

2. Клейнрок Л. Коммуникационные сети. – М.: Наука, 1970. – 255 с.

3. Клейнрок Л. Вычислительные системы с очередями. – М.: Мир, 1979. – 600 с.

4. Климов Г.П. Стохастические системы обслуживания. – М.: Наука, 1966. – 243 с.

5. Ковалев Е.А. Сети с ненадежными каналами и резервом // Математические методы исследования сетей связи и сетей ЭВМ. Тезисы докладов VI Белорусской школы-семинара по ТМО. – Минск, 1990. – С. 70–71.

6. Ковалев Е.А., Чикунова Н.А. Стационарное распределение двухузловой замкнутой ненадежной сети с делящимся резервом // Материалы международной конференции «Современные математические методы исследования телекоммуникационных сетей». – Минск, 1999. – С. 85–89.

7. Кофман А., Крюон Р. Массовое обслуживание. Теория и приложения. – М.: Мир, 1965. – 302 с.

8. Крыленко А.В. Сети массового обслуживания с несколькими типами заявок, немедленным обслуживанием и обходами узлов заявками // Проблемы передачи информации. – 1997. – Т. 33, Вып. 3. – С. 91–101.

9. Крыленко А.В. Малинковский Ю.В. Сети массового обслуживания с мгновенно обслуживаемыми заявками II. Модели с несколькими тинами заявок // Автоматика и телемеханика. – 1998. – №2. – С. 62–71.

10. Крыленко А.В., Малинковский Ю.В. Замкнутые сети массового обслуживания с обходами узлов и несколькими классами заявок // Becni Акад. навук Беларусi. Сер. ф1з.-мат. навук. – 1998. – №2. – С.

11. Крыленко А.В. Инвариантность стационарного распределения замкнутых сетей массового обслуживания с обходами узлов, неэкспоненциальным обслуживанием и несколькими типами заявок // Becni Акад. навук

12. Крыленко A.В., Малинковский Ю.В. Сети обслуживания с обходами и несколькими классами заявок // Исследование систем и сетей массового обслуживания: Тез. докл. 12‑й Бел. зимней школы-семинара по ТМО, Гр., 1996 г. / Бел. гос. унив. – 1996. – С. 48–49.

13. Крыленко А.В., Малинковский Ю.В. Замкнутые сети массового обслуживания с обходами узлов и несколькими классами заявок // VII Белорусская математ. конф. Тез. докл. науч. конф., Минск, 18–22 нояб. 1996 г. / Бел. матем. общ-во, Бел. гос. унив., Ин‑т матем-ки Академии наук Беларуси. – 1996.

14. Крыленко А.В. Инвариантность сетей массового ообслуживанием и обходами узлов заявками // Математические методы исследования телекоммуникационных сетей: Материалы 13‑й Бел. зимней школ. (науч. конф. BWWQT‑97), Минск, 3 – 1997 г. / Бел. гос. унив. – 1997. – С. 50–52.

15. Малинковский Ю.В. Критерий точечной независимости состояний узлов в открытой стационарной марковской сети обслуживания с одним классом заявок // Теория вероятностей и ее применения. – 1990. – Т.35, №4. – С. 779–784.

16. Малинковский Ю.В. Мультипликативность стационарного распределения открытых сетей обслуживания со стандартными узлами и однотипными заявками // Проблемы передачи информации. – 1999. – Том 35, Вып.1. – С. 96–110.

17. Малинковский Ю.В. Мультипликативность стационарного распределения состояний для одного класса сетей массового обслуживания // Автоматика и телемеханика. – 1988. – №2. – С. 108–118.