Навигация
Расчет числовых характеристик распределения случайных величин
2.2 Расчет числовых характеристик распределения случайных величин
Более полное, а главное, обобщенное представление о результатах эксперимента дают не абсолютные, а относительные (удельные) значения полученных данных. Так, вместо абсолютных значений числа экспериментальных данных ni, целесообразно подсчитать долю рассматриваемых событий в интервале, приходящихся на одно изделие (деталь, узел, агрегат или автомобиль) из числа находящихся под наблюдением, т.е. на единицу выборки. Эта характеристика экспериментального распределения называется относительной частотой (частостью) mi появления данного события (значений признака Xi):
![]() .
.
Относительная частота mi при этом, в соответствии с законом больших чисел, является приближенной экспериментальной оценкой вероятности появления события ![]() .
.
Значения экспериментальных точек интегральной функции распределения ![]() рассчитывают как сумму накопленных частостей mi в каждом интервале Ki. В первом интервале
рассчитывают как сумму накопленных частостей mi в каждом интервале Ki. В первом интервале ![]() во втором интервале
во втором интервале
![]()
и т.д., т.е.
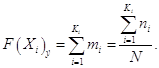
Таким образом, значение ![]() изменяются в интервале [0;1] и однозначно определяют распределение относительных частот в интервальном вариационном ряду.
изменяются в интервале [0;1] и однозначно определяют распределение относительных частот в интервальном вариационном ряду.
Другим удельным показателем экспериментального распределения является дифференциальная функция ![]() , определяемая как отношение частости
, определяемая как отношение частости ![]() к длине интервала
к длине интервала ![]()
![]()
и характеризующая долю рассматриваемых событий в интервале, приходящуюся на одно испытываемое изделие и на величину ширины интервала. Функция ![]() также еще называется плотностью вероятности распределения.
также еще называется плотностью вероятности распределения.
Полученные результаты расчета сводим в статистическую таблицу.
Таблица 2
Результаты интервальной обработки экспериментальных данных.
| Наименование параметра | Обозна- чение | Номер интервала, Ki | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Границы интервала | [a;b] | 14.5;24.5 | 24.5;34.5 | 34.5;44.5 | 44.5;54.5 | 54.5;64.5 | 64.5;74.5 |
| Середины интервала |
| 19.5 | 29.5 | 39.5 | 49.5 | 59.5 | 69.5 |
| Частота | mi | 8 | 6 | 8 | 6 | 2 | 2 |
| Относительная частота | | 0.25 | 0.1875 | 0.25 | 0.1875 | 0.0625 | 0.0625 |
| Накопленная частота |
| 8 | 14 | 22 | 28 | 30 | 32 |
| Оценка интегральной функции |
| 0.25 | 0.4375 | 0.6875 | 0.276 | 0.875 | 1 |
| Оценка дифференциальной функции |
| 0.025 | 0.04375 | 0.06875 | 0.0276 | 0.0875 | 0.1 |
Похожие работы
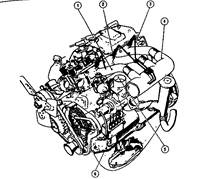
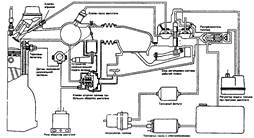
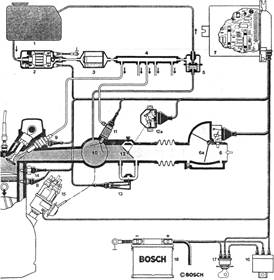
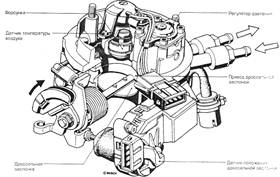
... присадками к топливу, промывка без демонтажа форсунок с помощью специальной установки и промывка на ультразвуковом стенде с демонтажом форсунок. 2. Исследование работы и процесса технической эксплуатации форсунок бензиновых двигателей 2.1 Конструкция электромагнитных форсунок Рассмотрим устройство и принцип действия форсунок на примере форсунки фирмы Бош, а также неисправности которые ...
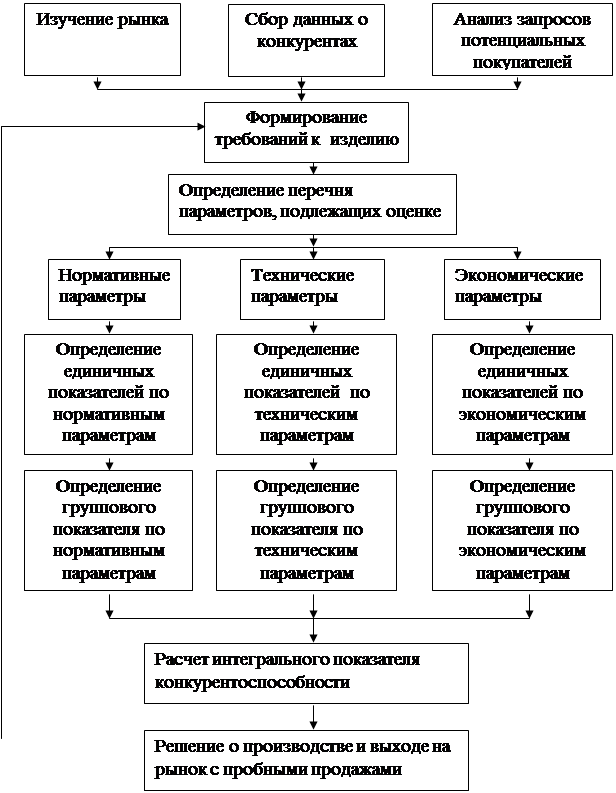
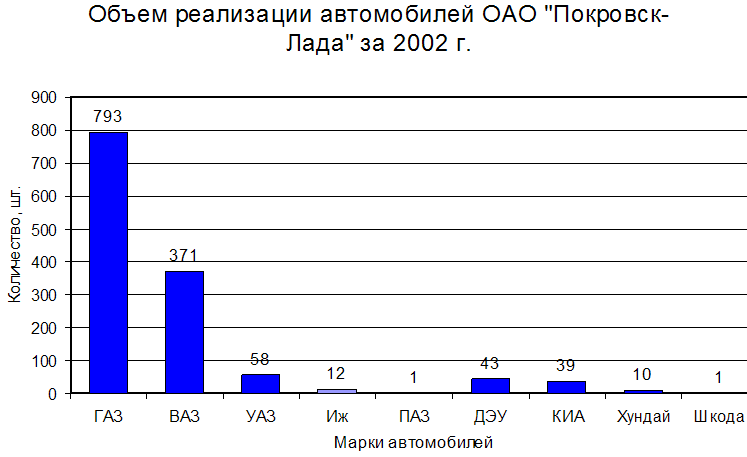
... . Дается реклама в газетах, на радио, по телевидению в виде бегущей строки и рекламного ролика. Так же выставляются рекламные щиты. 2.8. Оценка конкурентоспособности автомобилей, реализуемых ОАО «Покровск-Лада» Конкурентоспособность – важнейшая особенность товаров-конкурентов, базирующаяся на определенных принципах: комплексность, относительность, социальная адресность [9]. Комплексность ...
... итоговых корректировок Итоговая величина стоимости, полученная в результате применения всей совокупности ценовых мультипликаторов, должна быть откорректирована в соответствии с конкретными условиями оценки бизнеса. Наиболее типичными являются следующие поправки. Портфельная скидка представляется при наличии не привлекательного для покупателя характера диверсификации активов. Аналитик при ...
... тюнинга легкового автомобиля, приводятся технические требования к различным агрегатам автомобиля. Учебное пособие комплектуется демонстрационными материалами – фото тюнинговых автомобилей (5 шт.) Внешний тюнинг автомобилей Аэрография на автомобилях Глава 2. Тюнинг внедорожников Тюнинг для внедорожников это почти все то, о чем мы говорили в первой главе данной работы, за ...









0 комментариев