Навигация
Динамічні процеси та теорія хаосу
Курсова робота на тему:
Динамічні процеси та теорія хаосу.
ПЛАН
Вступ
1. Відображення і потоки
1.1. Три образи хаосу
1.2. Аттрактор Лоренца і хаос в рідині
1.3. Універсальне відображення для нелінійних коливань
1.4. Стохастичні аттрактори
2. Хаотичні коливання
2.1. Перемежана і перехідний хаос
2.2. Консервативний хаос
3. Фізичні експерименти з хаотичними системами
3.1. Хаос в пружній безперервній середі
3.2. Тривимірні пружні стрижні і струни
3.3. Хаос в матричному друкуючому пристрої
3.4. Нелінійні ланцюги
4. Фрактальні властивості хаосу
4.1. Фрактали
4.2. Фрактали і хаос
Висновок
Список використаної літератури
Вступ
Для багатьох вивчення динаміки почалося і закінчилося другим законом Ньютона F = mA. Якщо задані сили, що діють між частками, а також початкові положення і швидкості часток, то за допомогою достатнього великого комп'ютера можна передбачити рух або розвиток системи для будь-якого скільки завгодно пізнього часу. Проте поява великих комп'ютерів і швидких комп'ютерів не привела до обіцяної нескінченної передбаченості в динаміці. Було виявлено що рух деяких дуже простих динамічних систем не завжди можна передбачити на великий інтервал часу. Такі рухи були названі хаотичними, і їх дослідження привабило в динаміку деякі нові математичні ідеї.
Побутове поняття хаосу дуже древньо і часто асоціюється з безладним або некерованим фізичним станом або поведінкою людей. Хаос лякає. Правда, завжди залишається надія дізнатися потаєні сили або причини цього хаосу або пояснити, чому виявляються непередбачуваними події, на вигляд випадкові.
Отже, основна мета даної роботи полягає у вивченні моделей хаосу.
1. Відображення і потоки 1.1 Три образи хаосу
Простим прикладом динамічної моделі, що виявляє хаотичну поведінку є логістичне рівняння, або рівняння зростання популяції:
xn + 1 = axn - bx2n (1.1)
Перший член в правій частці описує зростання або народження, а нелінійний член ответствен за обмеження зростання, зв'язане, наприклад, з обмеженістю енергетичних або харчових ресурсів. Якщо нехтувати нелінійним членом (b = 0), то можна виписати явне вирішення лінійного рівняння, що виходить:
xn + 1 = axn; xn =x0 an (1.2)
Це рішення стійке при | а | < 1 і нестійкий при | а | > 1 . У останньому випадку з лінійної теорії виходить нереалістичне передбачення необмеженого зростання.
Нелінійну модель (1.1) зазвичай переписують в безрозмірному вигляді
xn + 1 = _xn (1 – xn) (1.3)
При _ > 1 є дві точки рівноваги (тобто х = _х (1 - х)). Для з'ясування стійкості відображення хn + 1 = f (хn) слід обчислити величину нахилу | f’ (x) | у точці спокою. Якщо | f’ | > 1, точка спокою нестійка. При 1 < _ < 3 логістичне рівняння (1.3) має дві точки спокою: х = 0, (_ — 1) /_; при цьому початок координат — нестійка крапка, а друга точка спокою стійка.
Проте при _ = 3 нахил при x = (_ — 1)/ _ перевищує одиницю (f' = 2 - _) і обидві точки рівноваги стають нестійкими. При значеннях параметра _, увязнених між 3 і 4, це просте різницеве рівняння описує безліч багатоперіодичних і хаотичних рухів. При _ = 3 стає нестійким стаціонарне рішення, але залишається стійким бицикл або двоперіодична орбіта. Ця орбіта показана на мал. 1.1. Величинах xn повторюється через кожну ітерацію.
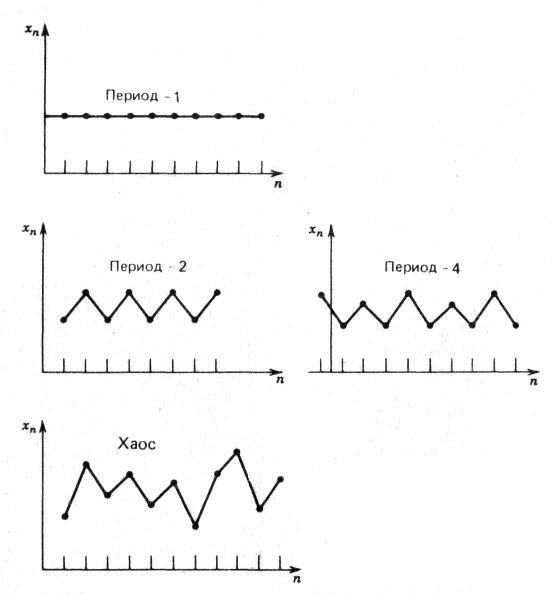
Рис 1.1. Можливі типи вирішень логістичного рівняння (1.3). Вгорі – стаціонарний рух з періодом 1; посередині - рух з періодом 2 і періодом 4; внизу – хаотичний рух.
При подальшому збільшенні _ двоперіодична орбіта стає нестійкою і виникає цикл з періодом 4, який унаслідок біфуркації швидко замінюється циклом з періодом 8 при ще більших значеннях _. Цей процес подвоєння періоду продовжується до тих пір, поки _ не досягає значення _: = 3,56994... . Поблизу цього значення послідовність значень параметра, при яких відбуваються подвоєння періоду, підкоряється точному закону
![]() (1.4)
(1.4)
Це граничне відношення називається числом Фейгенбаума — на ім'я фізики, який виявив ці властивості даного відображення.
При значеннях _, що перевищують _:, можуть виникати хаотичні ітерації, тобто поведінка моделі на великих часах не укладається в рамки простого періодичного руху. У інтервалі _:< _ < 4 також присутні певні вузькі інтервали s_, для яких існують періодичні орбіти. Хаотична орбіта логістичного відображення показана на мал. 2 за допомогою залежності х n+ 1 від хn.
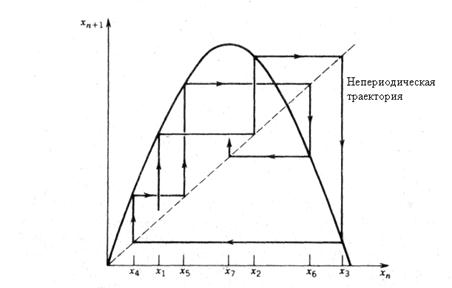
Рис. 1.2. Графічне вирішення різницевого рівняння першого порядку.
Роль цього відображення не лише в тому, що воно дає зразок хаосу. Було показано, що і інші відображення виду хп + 1 = f (xn), де f (x) — квадратична або складніша функція, поводяться приблизно так само, задовольняючи тому ж закону (1.4). Явище подвоєння періоду або регулярної зміни бифуркационного параметра називають універсальною властивістю певних класів одновимірних різницевих моделей динамічних процесів.
Подвоєння періоду і відношення Фейгенбаума (1.4) виявляються в багатьох фізичних експериментах. Це означає, що в багатьох безперервних еволюційних процесах зведення до різницевого рівняння за допомогою перетину Пумнкаре приводить до квадратичного відображення (1.1); звідси слідує важлива роль відображень в дослідженні диференціальних рівнянь.
1.2 Аттрактор Лоренца і хаос в рідиніУ 1963 р. фахівець з фізики атмосфери на ім'я Е.Н. Лоренц з Массачусетсського технологічного інституту запропонував просту модель теплової конвекції в атмосфері. Рідина, що підігрівається знизу, легшає і спливає, а важча рідина опускається під дією гравітації. Такі рухи часто організовуються в конвективні валики, подібні до рухів рідини в тривимірному торі, показаному на рис. 1.3.
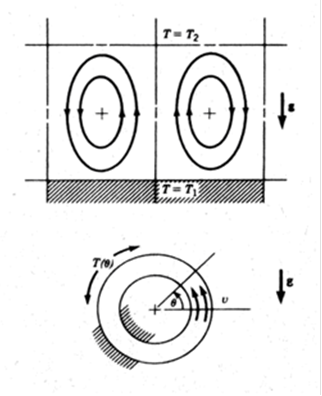
Рис. 1.3. Вгорі – схема ліній струму рідини в конвективному вічку при стаціонарному русі; внизу – одновимірна конвекція в кільцевій трубці під дією сили тяжіння і градієнта температури.
У математичній моделі конвекції, яку запропонував Лоренц, використовуються три змінні (х, біля, z), що описують стани системи. Змінна х пропорційна амплітуді швидкості, з якою рідина циркулює в рідкому кільці, а змінні біля і z відображають розподіл температури по кільцю. Так звані рівняння Лоренца можна формально отримати з рівняння Навьє — Стоксу, рівняння в приватних похідних механіки рідини. У безрозмірному виді рівняння Лоренца записуються таким чином:
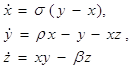 (1.5)
(1.5)
Параметри _ і ? пов'язані відповідно з числами Прандтля і Релея, а третій параметр d описує геометрію системи. Відзначимо, що єдині нелінійні члени — це хz і ху в другому і третьому рівняннях.
При _ = 10 і d = 8/3 (набір параметрів, що віддається перевага фахівцями в цій області) і при ? > 1 є три положення рівноваги, з яких те, яке розташоване на початку координат, є нестійкою седловой крапкою (рис. 1.4).
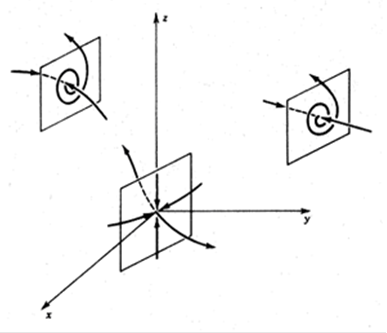
Рис 1.4. Локальні схеми руху поблизу трьох крапок рівноваги для рівнянь Лоренца (1.5).
1.3 Універсальне відображення для нелінійних коливань
Структура відображення. Рівняння ![]() (1.6), званий гамильтониан породжує рівняння руху
(1.6), званий гамильтониан породжує рівняння руху
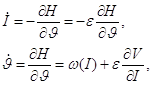 (1.7)
(1.7)
де необурена частота нелінійних коливань визначається вираженням
![]() (1.8)
(1.8)
Ці рівняння є диференціальними. Дискретна форма рівнянь руху у вигляді кінцевих різниць переважно для аналізу можливості появи стохастичності. Тому слід знатися на тому, як від рівнянь (1.7) перейти до їх різницевої форми і яка структура останніх.
Допустимо, що виділена деяка послідовність моментів часу t0, t1, t2 ..., і систему (1.7) удається звести до дискретної системи
![]()
яка зв'язує значення змінних (I ?) в двох послідовних моментах часу. Зручно ці рівняння записати в такій формі:
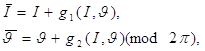 (1.9)
(1.9)
де індекс n опущений, межа стоїть замість індексу n + 1 і g1, g2 — функції, залежні від виду обурення. Надалі оператор (mod 2H) при фазі будемо, як правило, опускати.
Форма (1.9) є настільки спільною, що не містить ніякої інформації. У гамильтоновском випадку відображення (1.9) повинне зберігати міру, тобто повинна виконуватися умова
![]() (1.10)
(1.10)
Це означає, що
![]()
Для того, щоб система (1.9) знайшла який-небудь сенс, в неї слід вкласти фізичний зміст.
Хай змінна I є дією. Її зміна ![]() має бути пов'язане з деякою неадіабатичністю руху. У адіабатичному випадку, наприклад, sI експоненціально мало. У неадіабатичному випадку вважатимемо, що зміна дії в основному відбувається в деякій області часу st, в якій порушується адіабатична інваріантність. Повна зміна дії системи накопичується підсумовуванням різних окремих змін sI. Хай Т є характерний інтервал часу між двома послідовними областями порушення адіабатичної інваріантності. Це має на увазі нерівність
має бути пов'язане з деякою неадіабатичністю руху. У адіабатичному випадку, наприклад, sI експоненціально мало. У неадіабатичному випадку вважатимемо, що зміна дії в основному відбувається в деякій області часу st, в якій порушується адіабатична інваріантність. Повна зміна дії системи накопичується підсумовуванням різних окремих змін sI. Хай Т є характерний інтервал часу між двома послідовними областями порушення адіабатичної інваріантності. Це має на увазі нерівність
T > st (1.11)
яке відразу вирішує питання про те, як природним чином ввести відображення (1.9).
Якщо виконана умова (1.11), то існує природна структура відображення (1.9). Вона включає послідовність моментів {tk}, розділених інтервалами ~T між областями, де відбувається помітна зміна дії. Рівняння відображення виходять в результаті зшивання цих змін на двох послідовних інтервалах.
Вся відмінність в змінах дії поміщена у вигляді функцій g1, g2.
Ці прості міркування дозволяють без великих втрат виключити деякі непотрібні ускладнення. По-перше, вважатимемо, що st > 0, тобто зміна дії відбувається миттєво (удар). З фізичної точки зору це означає, що часовий інтервал st зміни дії менше всіх характерних часів завдання. По-друге, рахуватимемо інтервали T між моментами tk постійними.
Гамільтонін описаної системи може бути представлений в (p, x) -пространстве у вигляді
![]() . (1.12)
. (1.12)
На осцилятор з гамильтонианом H0 (p, x) діють миттєві поштовхи через постійні інтервали часу Т. Между поштовхами рух є вільним і передбачається відомим.
Тому зшивання рішень на двох різних інтервалах може бути проведена точно. Покажемо, як це лается.
Виведення відображення. Повернемося знову до змінних действие—угол:
![]() (1.13)
(1.13)
де V(I ?) виходить з V(х) заміною змінних. Рівняння руху (1.7) набирають вигляду
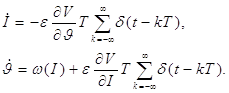 (1.14)
(1.14)
Хай поштовх відбувається при деякому t = t0. Визначимо -отображение таким чином:
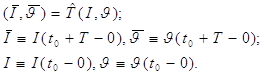 (1.15)
(1.15)
Відображення ![]() виникає як послідовна дія удару
виникає як послідовна дія удару ![]() і вільного руху (обертання на торі)
і вільного руху (обертання на торі) ![]() :
:
![]() (1.16)
(1.16)
(Мал. 1.5). Маємо для
![]() (1.17)
(1.17)
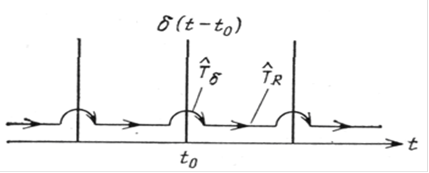
Рис. 1.5. Побудова універсального відображення.
Щоб отримати![]() , проінтегруємо систему (1.14) в малій околиці біля моменту поштовху (t0 - 0, t0 + 0). Врахуємо при цьому, що змінна x безперервна. Тому в крапці t0 функція V(x)= V(I ?) безперервна. Маємо
, проінтегруємо систему (1.14) в малій околиці біля моменту поштовху (t0 - 0, t0 + 0). Врахуємо при цьому, що змінна x безперервна. Тому в крапці t0 функція V(x)= V(I ?) безперервна. Маємо
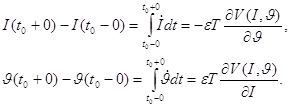 (1.18)
(1.18)
Рівняння (1.18) визначають ![]() :
:
![]() (1.19)
(1.19)
Підставляючи (1.17), (1.19) в (1.16), отримуємо рівняння (1.15) в явному вигляді:
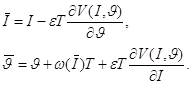 (1.20)
(1.20)
Це і є універсальне відображення. Воно допускає ще одне спрощення, якщо потенціал обурення залежить тільки від узагальненої координати ? і не залежить від імпульсу I. Тоді (1.20) перетворюється на наступне відображення:
![]() (1.21)
(1.21)
Остання модифікація пов'язана з вибором функції V(?). Це має бути періодична функція, і можна покласти V(?)= V0cos ?. Ще одне спрощення пов'язане з простим вибором функції ?(I): ? (I) = ?0 + ?’I. Це дає
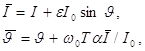 (1.22)
(1.22)
де позначено
![]() (1.23)
(1.23)
Рівняння (1.22) називають також стандартним відображенням зважаючи на його максимальну простоту.
Приведемо також вид гамильтониана, відповідного спрощеному відображенню (1.22):
![]() (1.24)
(1.24)
Лінійний член ?0I у гамильтониане H зникає при ?0 = 0. Квадратичний член по дії I при цьому залишається, оскільки через визначення (1.23) величина ??0 відмінна від нуля при ?0 = 0.
Структура фазового простору. Запишемо систему (1.22) в спрощеній формі, опустивши постійне зрушення фази ?0T і перейшовши до безрозмірної дії:
![]()
Отримуємо ![]() (1.25)
(1.25)
Нерухомі точки системи (1.25) знаходяться з рівнянь ![]() тобто
тобто
![]()
![]()
![]()
Звідси знаходимо особливі крапки
![]()
![]()
Точки r1 є нестійкими крапками. Поведінка траєкторій поблизу них показує, що ці точки гіперболічного типа.
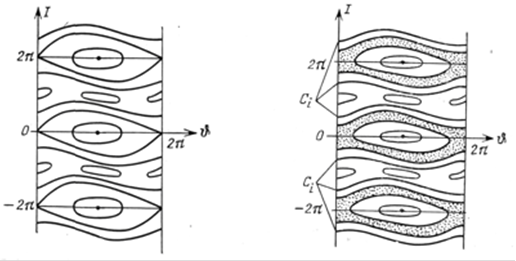
Рис. 1.6. Фазовий портрет стандартного відображення при малих значеннях K
Рис. 1.7. Фазовий портрет стандартного відображення при K : 1; Ci – інваріантні криві
Точки r2 є еліптичними, якщо К0 < 4. Фазовий портрет системи для малих K0 приведений на мал. 1.6. Із зростанням К0 в системі відбуваються біфуркації народження кратних періодів, а при K0 поблизу одиниці з'являється в околиці сепаратрисы широкий стохастичний шар (мал. 1.7). Різні стохастичні шари відокремлені один від одного інваріантними кривими, що існують унаслідок теореми Колмогорова—арнольда—мозера.
Стохастичне море. Подальше збільшення параметра K0 приводить до руйнування КАМ-КРІВИХ і злиттю стохастичних шарів. Утворюється стохастичне море, в якому, проте, існують острівці стійкості (мал. 1.8). Острівці залишаються завжди при будь-яких скільки завгодно великих значеннях K0. Їх розмір в цьому випадку має порядок 1/K0, а відображення (1.25) із зростанням К0 стає все ближчим до У-системе.
Наявність острівців стійкості є фундаментальною властивістю реальних фізичних систем. Все сказане вище без зусиль переноситься на універсальне відображення (1.20), і відзнака виражається кінець кінцем лише у формі і числі острівців.
Сама структура острівців також є незвичайно складною заплутаною картиною. Існують системи острівців різних порядків розмірів, що все більш і більш зменшуються (мал. 1.9). Утворення стохастичного шару відбувається в околиці сепаратрисы при K0 < 0,97, а в області значень K0 > 0,97 відбувається злиття стохастичних шарів з утворенням спільного стохастичного моря. Таким чином, область переходу до хаосу є дуже вузькою.

Рис. 1.8. Утворення стохастичного моря
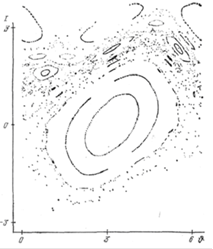
Рис. 1.9. Острівці різних порядків в стохастичному морі. Окремі, безладно розташовані крапки належать одній траєкторії
У міру подальшого зростання параметра K0 > 1 стохастичне море заповнює все велику частку фазового простору. В той же час острівці стійкості зменшуються в своїх розмірах. Одночасно зменшується і відносна міра острівців.
1.4 Стохастичні аттракториВідзначимо деякі істотні сторони появи стохастичності в негамильтоновских диссипативних системах. Існування дисипації приводить до зменшення фазового об'єму системи.
Фінітность руху. Наступне нижче зауваження перш за все відноситься до поняття локальної нестійкості. Очевидно, що поява цієї нестійкості формулюється настільки універсальним способом, що він не пов'язаний з конкретним детальним видом динамічної системи.
Хай, наприклад, рівняння руху має тривіальний вигляд:
![]()
![]() (1.26)
(1.26)
Його рішення
![]()
![]()
показує відразу нестійкість щодо обурень початкової умови:
![]() (1.27)
(1.27)
З іншого боку, очевидно, що, не дивлячись на властивість (1.27), ніякої стохастичності в системі (1.26) не немає. Парадокс пов'язаний з тим, що система (1.26) здійснює инфинитное рух, в якому траєкторії можуть розходитися достатньо далеко і достатньо швидко із-за необмеженості фазового простору.
Ситуація змінюється, якщо замість (1.26) розгледіти систему, фазовий простір якого фінітного
![]()
![]()
![]() (1.28)
(1.28)
Тут є стохастичність при K > 1. Дуже важлива умова, що накладається на розглядувані далі системи, — финитность їх динаміки у фазовому просторі. Цього зауваження набуває глибший сенс для диссипативних систем, де осциляторна динаміка може бути взагалі відсутньою. Зокрема, характеристичні показники можуть не мати уявної частки ні при яких реальних значеннях параметрів.
Аттрактори і репеллери. Порівняльний аналіз особливостей на фазовій плоскості для гамильтоновских і диссипативних систем якнайкращим способом представляє їх відмінність. Структура фазового простору в диссипативному випадку набагато багатша, і тому тут слід чекати різноманітнішу динаміку систем.
Однією з відмітних властивостей диссипативних систем є існування аттракторов і репеллеров. Під «аттрактором» розуміється будь-яка притягуюча безліч. Прикладами аттракторов можуть бути стійкий фокус, стійкий граничний цикл. «Репеллером» є відштовхуюча безліч крапок. Такою властивістю володіють, наприклад, нестійкий фокус і нестійкий граничний цикл. При t > : фазові траєкторії все ближче наближаються до аттрактору. Система наближається до деякого сталого режиму, точки якого належать безлічі А+, що є аттрактором. Аттрактор є інваріантна безліч, тобто
![]()
Репеллер легко зрозуміти, якщо представити його як аттрактор А-, до якого прагнуть фазові траєкторії при t > -. Він також є інваріантним безліччю:
![]()
Стохастичний аттрактор. На перший погляд здається, що існування аттракторов виключає можливість стохастичної динаміки у фазовому просторі, оскільки з часом відстань між крапками фазової траєкторії і точками безлічі А+ повинно прагнути до нуля. Тому з часом траєкторія все більше наближається до крапки або циклу, в структурі яких немає нічого випадкового. Природа, проте, розпорядилася інакше.
Існує притягуюча безліч, сама структура якої є дуже складною. Її не просто описати, але можна вказати її головну особливість. Динаміка крапки на такій структурі в будь-якому можливому для аналізу сенсі є випадковою подібно до того, як це має місце в гамильтоновских системах. Така притягуюча безліч, на якій реалізується стохастична динаміка, називатимемо стохастичним аттрактором. У поняття стохастичності вкладаються, по суті, ті ж не дуже строго певні поняття, що апелюють швидше до фізичного сенсу, чим до строгого визначення. Перерахуємо їх.
Похожие работы
... саме ідеї про біполярності, однополярності, багатополярності й інших комбінацій полярності пристрою світової системи. Предметом досліджень, проведених у рамках теорій неореалізму, є проблеми розподілу економічного впливу в системі міжнародних відносин як, детермінуючого фактора, глобальної політичної структури, що визначає у свою чергу, і структуру безпеки. Основний акцент у неореалізмі робиться ...
... тієї чи іншої політики уряду, указати на те, які зміни в поводженні споживача чи продавця можуть привести до більш сприятливого розвитку економіки. 4.3 Формування нового підходу до управління Роботи з теорії хаосу і теорії складності вплинули на теорію управління. Прикладом служить дуже популярна в останні роки книга П.Сенджа "П'ята дисципліна: мистецтво і практика пізнання організації". ...
... банківська, фінансова та податкова системи, власні гроші і національний бюджет, прикордонна та митна системи тощо. Але трансформаційні процеси в Україні не обмежуються перебудовою її соціально-економічного устрою. У сучасному світі міжнародне економічне життя перебуває на етапі глобалізації, тобто більшість країн втягнуто в єдиний економічний простір. Тому курс України на активне входження у сві ...
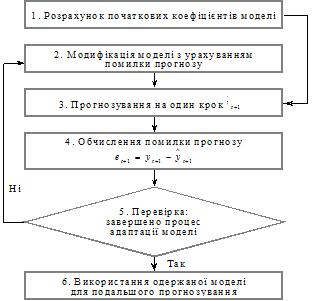
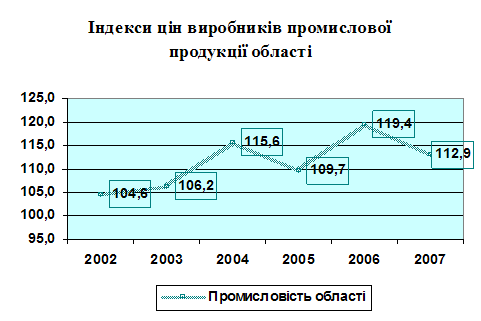
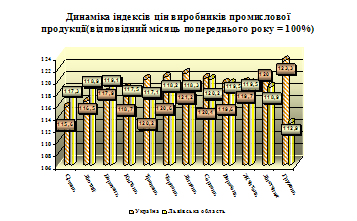
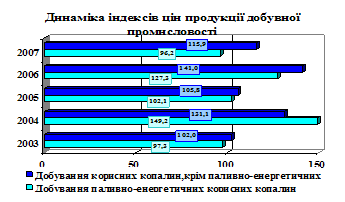
... ікативна модель дає неточні результати. У процесі побудови моделі виконують числову оптимізацію параметрів адаптації в межах [0; 1]. РОЗДІЛ 3 СТАТИСТИЧНА ОЦІНКА ТА ПРОГНОЗУВАННЯ ЦІН НА ПРОМИСЛОВУ ПРОДУКЦІЮ У ЛЬВІВСЬКІЙ ОБЛАСТІ 3.1 Статистичний аналіз цін виробників промислової продукції у Львівській області У Львівській області індекс цін виробників промислової продукції у 2007 році ...
0 комментариев