Дедуктивные умозаключения

ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ

 

ПЛАН

 

1.         Внутренняя структура элементарных суждений. Логический квадрат

2.         Непосредственные умозаключения

3.         Категорический силлогизм

4.         Полисиллогизмы

5.         Энтимемы. Логика общения и спора

6.         Сориты и эпихейремы

Литература

1. ВНУТРЕННЯЯ СТРУКТУРА ЭЛЕМЕНТАРНЫХ СУЖДЕНИЙ. ЛОГИЧЕСКИЙ КВАДРАТ

Элементарное суждение состоит из двух понятий S и P соединённых с помощью связок «есть», «не есть». Понятие S , отображающее предмет мысли суждения, называется субъектом суждения, а понятие P, в котором высказывается, что собой представляет субъект S , - предикатом суждения. Если предикат относится ко всему объему субъекта, то это выражается словами «Все S », если же только к его части, то «Некоторые S ». Так что S и P могут объединяться в четыре вида суждений:

1.         Общеутвердительные суждения. Они символически обозначаются ASP или, еще короче, А. Это читается так: «Все S суть P ». Схематически соотношение между S и P изображается так:

Р

или так

2.         Общеотрицательные суждения. Они символически обозначаются ESP или, еще короче, Е. Это читается: «Все S не есть P ». Диаграммы Эйлера для S и Р имеет вид:

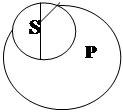
3.         Часто утвердительные суждения. Они символически обозначаются ISP или, еще короче, I. Это читается так: «Некоторые S есть P». Диаграммы Эйлера для S и Р имеет вид:

или вид,

где заштрихованная часть изображает общие элементы объемов S и Р.

4.         Частноотрицательны суждения. Они символически обозначаются OSP или, еще короче, О. Это читается: «Некоторые S не есть Р». Диаграммы Эйлера для S и Р имеет вид:

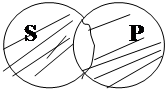где заштрихованная часть изображает несовпадающие элементы S и Р.

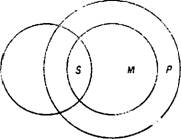
Вообще, вопрос, сколькими возможными способами могут быть связаны два понятия Х и У в суждениях, решается с помощью диаграмм Эйлера. Объемы понятий Х и У могут быть связаны одними и только одним из пяти способов:

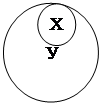
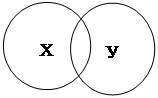
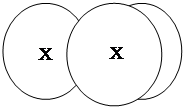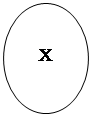
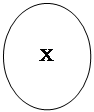
Выписывая под каждой из диаграмм четыре категорических суждения мы получим все взаимоисключающие способы, которыми могут быть логически связаны два понятия Х и У в суждения.

А х у	А ху	A yx
I xy	A yx	I xy
I yx	I xy	I yx
O yx	I yx	O xy

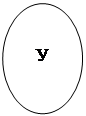I xy	E xy
I yx	E yx
O xy	O xy
O yx	О yx

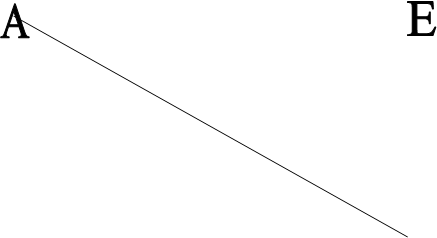
Византийский логик Михаил Пселл предложил наглядную схему, облегчающую запоминание характера взаимоотношений между истинным значением четырех видов суждений A, E, I, O, образованных из понятий S и P. Она получила название логического квадрата и выглядит так:

Противные суждения, например, суждения «Все учащиеся нашего класса - отличники», «Ни один учащийся нашего класса не отличник» не могут быть одновременно истинными. Но оба они могут оказаться ложными, так как между ними есть третье суждение: «Некоторые студенты нашего класса – отличники».

Одно из противоречащих суждений обязательно истинно, а другое ложно. Например, суждение «Все жиры растворяются в воде» ложно, тогда как противоречащее ему суждение «Некоторые жиры не растворяются в воде» истинно. Равно как суждение «Все жиры не растворяются в воде» истинно, а суждение «Некоторые жиры растворяются в воде» ложно.

Истиностное значение подчиненных суждений определяется следующими правилами:

1.         Из истинности общего суждения следует истинность подчиненного ему суждения. Так, суждение «Все деревья поглощают углекислоту» истинно, а потому истинно и суждение «Некоторые деревья поглощают углекислоту».

2.         Из ложности частного суждения следует ложность подчиняющего его общего суждения. Из ложности суждения «Некоторые млекопитающие хладнокровны», вытекает ложность суждения «Все млекопитающие хладнокровны», равно как из ложности суждения «Некоторые киты не живут в воде» вытекает ложность суждения «Все киты не живут в воде».

3.         Из истинности частного суждения не следует с необходимостью истинность подчиняющего общего суждения. Так, из истинности суждения «Некоторые студенты нашей группы хорошо учатся» вовсе не вытекает истинность суждения «Все студенты нашей группы хорошо учатся».

4.         Из ложности общего суждения нельзя выводить ни необходимой ложности, ни необходимой истинности подчиненного суждения. Так, из ложности суждения «Все учащиеся нашего класса – отличники» нельзя сказать будет ли истинным или ложным суждение «Некоторые учащиеся нашего класса – отличники».

Истиностное значение подпротивных суждений подчиняется следующим правилам:

1. Из истинности одного подпротивного суждения не вытекает ложность другого подпротивного суждения. Так из истинности суждения «В некоторых селах нашей области есть стадионы», не вытекает ложность другого подпротивного суждения «В некоторых селах нашей области нет стадионов». Оба подпротивных суждения могут быть истинными.

1.         Если одно из подпротивных суждений ложно, то другое истинно. Если ложно суждение «В некоторых селах нашего района есть дворцы культуры», то истинно суждения «В некоторых селах нашего района нет дворцов культуры».

2.         Оба подпротивных суждений не могут быть одновременно ложными, одно из них обязательно истинно.

2. НЕПОСРЕДСТВЕННЫЕ УМОЗАКЛЮЧЕНИЯ

 

Непосредственными умозаключениями являются такие умозаключения, в которых вывод делается из одной посылки. Таким будет, например вывод. «Все простые числа делятся на себя и на единицу. Следовательно, ни одно простое число не делится на два». Непосредственные умозаключения схематически можно записать так: CSP→Y ав, где Х и У могут иметь значение A, E, I, O, а а и в – значение либо S либо P. Суждение CSP называется условием (или антецедентом), а Y ав называется заключением или следствием (или консеквентом). Имеется четыре способа выбора Х, четыре способа выбора У и два способа выбора а и в. значит число модусов (фигур) непосредственных умозаключений равняется 4х4х2=32. Однако не все из них истинны. Некоторые из них ложны. Под истинным значением модуса следует понимать «всегда истинен», а под ложностью «не всегда истинен».

Истинность каждого модуса может быть установлена с помощью логического квадрата и таблицы истинности импликации. Например, модус ASP→ESP ложен. В самом деле, если суждение ASP истинно, то по правилу логического квадрата суждение ESP ложно и импликация ложна.

Истинность модуса может быть установлена и с помощью диаграмм Эйлера. Модус истинен, если диаграмма Эйлера, изображающая связь предиката и субъекта условия, совпадает с диаграммой, изображающей связь субъекта и предиката следствия. Так для модуса ASP→ESP диаграмма условия имеет вид:

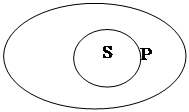
А диаграммы следствия –

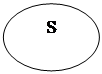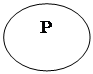они не совпадают. Значит, модус ложен.

Легко убедится, что, например, модус ASP→ISP истинен. В самом деле, по правилу логического квадрата если истинно общее суждение, то истинно и подчиненное ему суждения, а если оно ложно, то ложно и подчиненное суждение. Посылка и заключение тем самым имеют одно и то же истинное значение, а значит импликация всегда истинна. Диаграмма Эйлера для условия имеет вид:

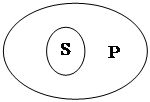
А для следствия – вид:

Они совпадают.

Чтобы выделить истинные модусы можно воспользоваться и правилами распределения членов суждения, т.е. S или P. Некоторый член суждения (т.е. S или P) называется распределенным тогда, когда он является либо субъектом общего суждения, либо предикатом отрицательного суждения. Так, в суждении АSР субъект S распределен, а предикат P - не распределен. В суждении ESP распределены и субъект, и предикат. В суждении ISP не распределены ни субъект, ни предикат. Наконец, в суждении OSP субъект не распределен, а предикат распределен.

Итак, для истинных модусов непосредственных умозаключений выполняются два правила: