В любом истинном модусе суждения являются либо оба утвердительными, либо оба отрицательными

1.         В любом истинном модусе суждения являются либо оба утвердительными, либо оба отрицательными.

2.         В любом истинном модусе каждый распределенный член в его заключении распределен и в его условии.

Рассмотрим, например, модус ASP ® APS. Член Р распределен в заключении, но он нераспределен в следствии. Значит, модус ложен.

Любым из указанных методов легко установить, что из 32 модусов непосредственных умозаключений только 10 истинны. Отбрасывая из этих десяти четыре тавтологии XSP®XSP, где Х может принимать одно из значений A,E,I,O, получаем шесть истинных модусов:

ASP ® ISP;

ESP ® OSP;

ASP ®IPS;

ESP ®EPS;

ESP ®OPS;

ISP ®IPS.

Модусы ASP ® ISP и ESP ® OSP называются изменением количества суждений. Их примерами могут служить заключения: «Все прилагательные обозначают признак предмета, значит, некоторые прилагательные обозначают признак предмета»; «Все жиры не растворяются в воде. Следовательно, некоторые жиры не растворяются в воде».

Модусы ASP ®IPS, ESP ®EPS, ESP ®OPS, ISP ®IPS называются обращением. При обращении субъект и предикат посылки меняются местами: в заключении субъект становится предикатом, а предикат – субъектом. Примерами этих модусов могут быть заключения: «Все звезды – небесные тела, следовательно, некоторые небесные тела – звезды»; «Ни одна ель не есть лиственное дерево. Следовательно, ни одно лиственное дерево не есть ель»; «Некоторые изобретатели – инженеры. Значит, некоторые инженеры – изобретатели» и т.д.

3.         КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ

 

Категорический силлогизм – это умозаключение, в котором из двух простых (категорических) суждений (они называются посылками), связанных общим понятием (его обозначают через М и называют средним термином) выводится третье суждение, называемое выводом; при этом средний термин в заключение не входит.

По определению силлогизм имеет схему:

X_в,а Ù Y_c,в ® Z_c,а ,

где X, Y, Z могут иметь смысл A, E, I, O; в, а - принимать значение М или Р; с, в – значение S или М; с, а - значение S или Р.

Имеется 4 способа выбора Х, 4 – выбора У, 4 – выбора Z, 2 способа выбора в, а и 2 способа выбора с, в. Значит, имеется 4•4•4•2•2═256 различных модусов силлогизма.

Составляющая любого модуса силлогизма принято обозначать так:

суждения, из которых делается вывод, называются посылками;

посылка, содержащая Р, называется большой посылкой;

посылка, содержащая S – малой.

Понятия, входящие в силлогизм, именуются терминами;

Р – называется большим термином;

S – малым термином;

М – средним термином;

S и Р – крайними терминами.

Суждение, не содержащие М и составляющее вывод, называется заключением силлогизма.

Средний термин М в посылках может стоять либо на первом, либо на втором месте. Так, что имеется четыре фигуры силлогизма. Наглядно их можно изобразить графически и символически так:

1. М — Р

S—М либо CMRÙUSM→ZSP

S— Р

2.         Р — М

S—М либо CRМÙUSM→ZSP

S— Р

3. М — Р

М—S либо CMRÙUМS→ZSP

S— Р

4. Р — М

М—S либо CRМÙUМS→ZSP

S— Р

Здесь Х, У, Z, могут иметь смысл А, Е, І, О. Так, что каждая фигура силлогизма имеет 64 модуса.

Не все модусы каждой фигуры истины. Истинность или ложность модуса легко проверить с помощью диаграмм Эйлера: модус истинен, если диаграмма S и Р посылок совпадает с диаграммой S и Р следствия; в противном случае он ложен, т.е. не всегда истинен. Так для модуса AMRÙESM→ESP диаграмма S и Р посылок имеет вид:

А для следствия – вид:

 

Эти диаграммы не совпадают. Значит, модус ложен. Напротив, для модуса EMPÙASM→ESP диаграмма S и Р посылок имеет вид:

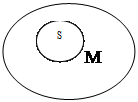А для следствия – вид:

диаграммы совпадают. Значит, этот модус истинен.

Существуют три правила, с помощью которых легко установить истинность или ложность силлогизма той или иной фигурой.

1.         В каждом истинном модусе число отрицательных посылок равно числу отрицательных следствий.

2.         В каждом истинном модусе термин, распределенный в следствии, распределен и в одной из посылок.

3.         В каждом истинном модусе средний термин распределен в одной из посылок.

С помощью диаграмм Эйлера или этих правил устанавливается, что имеется 24 истинных модуса силлогизма по 6 в каждой фигуре. Вот эти модусы:

Модусы 1 фигуры:

AMPÙASM→ASP

ЕMPÙASM→ЕSP

AMPÙISM→ISP

EMPÙISM→OSP

AMPÙASM→ISP

EMPÙASM→OSP

Модусы 11 фигуры:

EPMÙASM→ESP

APMÙESM→ESP

EPMÙISM→OSP

APMÙOSM→OSP

EPMÙASM→OSP

APMÙESM→OSP

Модусы 111 фигуры:

AMPÙAMS→ISP

IMPÙAMS→ISP

AMPÙIMS→ISP

EMPÙAMS→OSP

OMPÙAMS→OSP

EMPÙIMS→OSP

Модусы 1У фигуры:

APMÙAMS→ISP

APMÙEMS→ESP

IPMÙAMS→ISP

EPMÙAMS→OSP

EPMÙIMS→OSP

APMÙIMS→OSP

Приведем наглядные примеры истинных модусов фигур силлогизмов.

Первая фигура.

Все щелочноземельные металлы (М) двухвалентны (Р).

Стронции (S) – щелочноземельный металл (М).

Стронции (S) - двухвалентный (Р).

Вторая фигура.

Всякое растение (Р) содержит клетчатку (М).

Ни одна гидра (S) не содержит клетчатки (М).

Ни одна гидра (S) не растение (Р).

Третья фигура.

Все бамбуки (М) цветут один раз в жизни (Р).

Все бамбуки (М) – многолетние растения (S).

Некоторые многолетние растения (S) цветут один раз в жизни (Р).

Четвертая фигура.

Все киты (Р) – млекопитающие (М).

Ни одно млекопитающее (М) не есть рыба (S).

Ни одна рыба (S) не есть кит (Р).

4. ПОЛИСИЛЛОГИЗМЫ

Силлогизм является элементарным умозаключением. Он не разложим на другие, более элементарные умозаключения. Доказательства в повседневном общении и науках представляют собой целые цепочки силлогизмов и притом такие цепочки, в которых заключение каждого предшествующего силлогизма становится одной из посылок последующего. Такие цепочки силлогизмов называются полисиллогизмами.

Полисиллогизмы, в которых заключение предшествующего силлогизма становится большой посылкой последующего силлогизма, называются прогрессивными.

Прогрессивным будет, например, силлогизм.

1. Все законы естествознания имеют объективный характер.

Все законы физики – законы естествознания.

Все законы физики имеют объективный характер.

2.         Все законы физики имеют объективный характер.

Законы квантовой механики – законы физики.

Законы квантовой механики имеют объективный характер.

В регрессивных полисиллогизмах заключение предшествующего силлогизма являются меньшей посылкой последующего. Приведем пример регрессивного полисиллогизма.

1.         Все киты – млекопитающие.

Все дельфины – киты.

Все дельфины – млекопитающие.

2.         Все млекопитающие – позвоночные.

Все дельфины – млекопитающие .

Все дельфины – позвоночные.

5. ЭНТИМЕМЫ. ЛОГИКА ОБЩЕНИЯ И СПОРА

 

В практике повседневного мышления и в научных рассуждениях часто одна из посылок силлогизма или заключение пропускается. Они не формулируются явно и лишь подразумеваются. Такие силлогизмы называются энтимемами. Вот лишь некоторые примеры энтимемы: мы не строим силлогизм для доказательства электропроводности меди, а просто говорим: «Медь металл, а значит, она электропроводна». В этом рассуждении пропущена, но подразумевается большая посылка «Все металлы электропроводны». Аналогично в рассуждении «Всякое ремесло полезно, а значит слесарное дело полезно» опущена малая посылка «Слесарное дело – ремесло».

Энтимемы почти неизбежны. Без них существенно замедлился бы обмен мыслями, сделавшись невыносимо скучным. С полным правом можно опускать то, что очевидно. В противном случае наши слушатели разбегутся. Есть такие посылки, которые очевидны в данном доводе потому, что они хорошо известны и общеприняты, или потому, что мы о них уже говорили. Обратно, если действительно можно опустить какую-либо посылку без ущерба для ясности, оставшаяся часть доказательства должна более или менее сразу подсказывать, что именно подразумевается. Поэтому и можно ее подразумевать молча.

Однако не всегда использование полного силлогизма является признаком щегольства логической точностью и правильностью. Искусные ораторы часть пользуются энтимемами для того, чтобы отвлечь внимание слушателя от той посылки, истинность которой он мог бы поставить под сомнение. В этих случаях необходим логический анализ, включающий поиск недостающих посылок и заключений. Этот анализ, конечно же, будет неоднозначным, потому, что можно по-разному добавлять недостающие посылки и по-разному их толковать. Так возникают споры и дискуссии. Например, если кто-то убеждает нас, что Америка – богатая страна, потому, что в ней каждую минуту совершается грабеж, и мы поставили этот вывод под сомнение, то мы должны восстановить рассуждение оппонента до полного силлогизма. Он будет выглядеть так:

Все страны, в которых каждую минуту совершается грабеж, богатые.

Нагония – страна, в которой каждую минуту совершается грабеж.

Нагония – богатая страна.

Поставив под сомнение первую посылку, мы поставим под сомнение и все рассуждение оппонента.

Часто в общении мы высказываем суждения, образующие (как правило, вместе с другими очевидными) посылки для вывода умозаключения, которые мы предпочитаем не высказывать прямо. Тогда мы вступаем на почву намеков. Например, если кто-то может нас угостить кофе, и мы знаем, что он сделает это, если ему станет известно, что мы устали, нам достаточно сделать намек: «Ох, как я устал».

 

6. СОРИТЫ И ЭПИХЕЙРЕМЫ

Если пропускается какие-то посылки в полисиллогизме, то такое заключение называется соритом.

Строение сорита выражается следующей формулой:

Все А – В

Все В – С

Все С – Д

Все Д – Е

Все К – М

Все А – М

Если пропускает меньшая посылка то такой сорит называется аристотелевским. Его пример:

3 – нечетное число.

Все нечетные числа – натуральные числа.

Все натуральные числа – рациональные числа.

Все рациональные числа – действительные числа.

3 – действительное число.

Если пропускается большая посылка, то такой сорит, называется гоклиеновским. Его пример:

Все рациональные числа – действительные числа.

Все натуральные числа – рациональные числа.

Все нечетные числа – натуральные числа.

3 – нечетное число.

3 – действительное число.

Эпихейрема – это такой силлогизм, в котором посылками являются энтимемы. Схема эпихейремы такова:

M есть P, так как оно есть N

S есть M, так как оно есть O

S есть P

Первая посылка могла бы быть построена следующим образом:

Все N суть Р

Все М суть N

Все М есть P

Вторая посылка могла бы быть выражена следующим образом:

Все О суть М

Все S суть O

Все S суть M

И схема заключения следующая:

Все М есть Р

Все S суть M

Все S суть Р

Пример эпихейремы.

Все ромбы – параллелограммы, так как они (ромбы) имеют попарно параллельные стороны.

Все квадраты ромбы, так как они (квадраты) имеют взаимно перпендикулярные диагонали, делящиеся в точке их пересечения пополам.

Все квадраты – параллелограммы.

Имеют место следующие правила для соритов. В каждом истинном модусе:

1.         Только последняя посылка может быть отрицательна, и только первая может быть частным суждением.

2.         Посылка отрицательна тогда, когда отрицательно следствие.

3.         Если какая-либо из посылок является частным суждением, то следствие также является частным суждением.

ЛИТЕРАТУРА

1.         Логика. К. - Хатнюк В.С. 2005 г.

2.         Логика – исскуство мышления. Тимирязев А.К.– К. 2000 г.

3.         Философия и жизнь – журнал- К. 2004 г.

4.         История логики и мышления – Касинов В.И. 1999.

5.         Логика и человек – М. 2000.

6.         Философия жизни. Матюшенко В.М. – Москва – 2003 г.

7.         Философия бытия. Марикова А.В. – К. 2000 г.