Для фотоизомеризации соединения А предложен следующий механизм процесса

21. Для фотоизомеризации соединения А предложен следующий механизм процесса

k₁

А+hν → А*

А* → А + hν'

k₃

 А* + А <=>А₂

 k_-3

Найдите выражение для квантового выхода продукта А₂. Зависит ли квантовый выход от интенсивности поглощенного света?

k₁k₃[А] - k_-3k₂[А]I^-1

Ответ: γ= —————————

k₂+ k₃[А]

22. Для определения числа поглощенных квантов энергии соединением НХ_(г) в актинометре используют следующую реакцию

HN₃ + Н₂0 + hv → N₂ + NH₂OH.

Концентрация азота в растворе равна 43,1 ·10^-5 М до облучения и 51,2 • 10^-5 М после 30 мин пропускания света.

A. Рассчитайте число квантов энергии, поглощенных в 1 с со единением НХ_(Г), зная, что объем актинометра равен 1 л.

Б. Оцените квантовый выход процесса, если известно, что при поглощении количества квантов, найденных в п. А, разлагается 0,158·10^-3 моль НХ.

B. Согласуется ли полученное значение квантового выхода с величиной, рассчитанной для следующего механизма реакции

 

НX + hv→Н· + X

Н· + НХ→Н₂ + Х

Х + Х→Х₂.

Ответ: А.0,45·10^-7 Эйнштейн·с^-1 . Б. γ=1,95. В. γ = 2

Глава 3. Кинетика гетерогенных реакций

 

3.1 Примеры

3.1.1. Образец сплава металла А и В длиной 0,5 см и образец металла В длиной 0,5 см спаяны друг с другом. Определите время, за которое в результате диффузии А из сплава в чистый слиток В на расстоянии от спая 0,01 и 0,2 см установится относительная концентрация А (с_А/с₀), равная 0,2, и D=const=2·10^-9 см²/с.

Решение: Для определения времени диффузии используем уравнение Фика . Вначале вычисляем t для х=0,01 см, предварительно определив Z по уравнению

с/с₀ = ^½(1-erfZ); 0,2=^1/2(erfZ); erfZ=0,6~Z

Затем вычисляем время по уравнению

x x 0,01

Z = ————; √t= ——— = —————; t=9,6 ч.

2√Dt Z2√D 0,6·2√2·10^-9

Проверяем надежность полученных результатов и применимость уравнения Фика. Для этого подставляем найденные величины в уравнение

0,5≥5,6√2·10^-9·9,6·3600≥0,046

Условия применимости уравнения выполняются, так как l(x_max)>5,6√Dt.

Повторяем расчет и вычисляем t для х = 0,2 см:

0,2

Z=06 = —————— ; t=3875 ч.

2√2·10^-9

Проверяем применимость уравнения для х = 0,2 см:

0,5 ≥ 5,6 √2-10^-9·3875·3600 ≥0,93.

Условие применимости уравнения не выполняется: l (х_та%) <с 5,6√Dt. Последний результат не надежен.

3.1.2. Рассчитайте время, за которое ширина диффузионной размы той зоны между сплавом АВ и металлом В станет равной 0,1см и D= const = 2-Ю-⁹ см²/ с.

Решение, Ширина диффузионной размытой полосы δ при диффузии в бесконечно протяженном теле (расстояние между фронтами диффузии) равна 2L или

δ = 2L = 2·5,б√Dt; 2,56√2.10^-9t =0,1; t=11 ч.

3.1.3. На дно цилиндрического сосуда, залитого водой, помещен слой сахара. Сахар, растворяясь, диффундирует в объем раствора. Над сахаром раствор насыщен и концентрация его с₀ постоянна. Высота столба жидкости 20 см. Вычислите, на каком растоянии х от границы раздела сахар—раствор относительная концентрация с/с₀ станет рав ной 0,8 через 16 сут; D=0,25 см²/сут. Учтите, что для данных условий (t, D), согласно уравнению , l = 11,2 см при 298 К.

Решение. Поскольку происходит нестационарная диффузия в полубесконечном пространстве, то для расчета используем уравнения :

0,8 = (1— erfZ); erf Z=0,2; Z = 0,2;

0,2 = х/2 √0,25·16; x = 0,8см.

1-е уравнение применимо для данных условий, так как l > х (11,2 > 0,8).

3.1.4. На дно цилиндрического сосуда, залитого водой, помещен слой сахара. Сахар, растворяясь, диффундирует в объем раствора. Над сахаром раствор насыщен и концентрация его с₀ постоянна. Высота столба жидкости 20 см и D = 0,25 см²/сут. Рассчитайте количество са хара, которое перейдет в раствор с 1 см² поверхности за 16 сут, если с₀ = 2,565 моль/л.

Решение. Число молей сахара, растворившегося за 16 сут, рассчитываем по уравнению :

2c_s D 2·2,565 0,25

J = —— √— = ———— √—— = 2,61·10^-4

√π t 1000 16

моль/(сут·м²)

∆n = Jt =2,61·10^-4·16 = 5,776·10^-3 моль·cм²

m_сахара =5,776·10^-3·342,3 = 1,977 г/см²

3.1.5. Рассчитайте радиус молекулы белка, если его коэффициент диффузии в растворе сахара D= 6,39·10^-7 см²/с, Т = 298 К. Считайте, что молекулы белка имеют сферическую форму.

Решение. Радиус молекулы белка рассчитываем по формуле

 RT

r= ————

DN_A

где n= 1,227·10-³ Па·с [М];

(8,314Дж/(моль·К))(298К)

r= ————————————————— =

(6,39·10^-11м²/с)(6,02·10²³)6·3,14(1,227·10^-3Па·с)

= 2,79·10^-9м.

3.1.6. Таблетка бензойной кислоты с площадью поверхности S= 2 см² помещена в раствор бензойной кислоты. Объем раствора 20 л, концентрация 0,003 моль/л. Раствор размешивали, в результате чего за 5 мин растворилось 0,001 моль C₆H₅COOH. Можно принять, что практически концентрация раствора при этом не изменилась. Концентрация кислоты в насыщенном растворе c_s = 0,024 моль/л (298 К). Коэффициент диффузии бензойной кислоты D ='0,75 см²/сут. Вычислите константу скорости растворения k, скорость диффузии β, толщину приповерхностного слоя δ.

Решение. На границе приповерхностного слоя и поверхности таблетки концентрация постоянна и равна с₈. Концентрация в массе раствора в течение рассматриваемого времени тоже постоянна, поэтому поток вещества через приповерхностный слой можно считать стационарным и

dc ∆c  c_s-c

——— = —— = ———

dx ∆x δ

Для стационарного потока уравнение принимает вид

dn ∆n DS

—— = —— = —— (c_s-c)

dt t δ

Константы скорости рассчитываем по следующему уравнению, для чего находим. DS/δ:

DS ∆n 0,001·60·24

——— = ———— = —————— = 13714 см³/сут

δ t(c_s-c) 5(0,024-0,003)

Подставляем числа для нахождения k и β

13714 D 13714

k= ——— = 0,6857 сут^-1; β = —— = ——— 6857 см/сут

20·10³  δ 2

DS 0,75·2

δ= ———— = ———— = 1,09·10^-4 см

13714 13714

3.1.7 Концентрация кислоты в насыщенном растворе c_s = 0.024 моль/л (298 К). Коэффициент диффузии С₆Н₅СООН D=0,75 см²/сут. Концентрация раствора в ходе растворения изменялась. Таблетка бензойной кислоты с площадью поверхности S=2 см² помещена в раствор бензойной кислоты.

.

Объем раствора 20 л, концентрация 0,003 моль/л. Раствор размешивали, в результате чего за 5 мин растворилось 0,001 моль С₆Н₅СООН. Определите время, за которое концентрация раствора станет равной 0,012 моль/л.

Решение. Поскольку концентрация раствора в рассматриваемом отрезке меняется, меняется и градиент концентраций в приповерхностном слое, т. е. процесс диффузии нестационарен. Используем уравнение. Так как

2,3 c_s-c₁

t₁ =0; c₁=0,003, то k = —— lg———

 t₂ c_s-c₂

Подставляем числа и решаем относительно t;

2,3 0,024-0,003

t₂ = —— lg————— = 0,815 сут, или 19,55 ч.

0,6857 0,024-0,012

3.1.8. Металлический цинк площадью 20 см² при 298 К растворяли в 700 см³ серной кислоты по уравнению

Zn + H₂S0₄= ZnS0₄+ Н₂

Вычислите скорость диффузии β и соотношение толщины диффузионных слоев (δ₁/δ₂) в опытах 1 и 3, используя следующие данные: Скорость перемешивания 400 об/мин.

Опыт ……… 1 2

τ, ч………………0 0,5 1

с_H2SO4, г-экв/л……0,153 0,118 0,090

Скорость перемешивания 216 об/мин

Опыт…………….. 3

τ, ч………………... 0 0,5

с_H2SO4, г-экв/л…… 0,080 0,069

Решение: Определяем константу скорости растворения. При t=0

 

2,3 c_t=0

k= ——— lg———

t₂ c_t

 

Определяем скорость диффузии β для опыта 1:

2,3 0,153

k₁₌ —— lg——— = 0,519 ч^-1

 0,5 0,118

Vk 700·0,519

β= —— = ———— 18,27 см/ч

S 20

 

Для опыта 3:

2,3 0,080

k₃ = —— lg——— 0,296 ч^-1

0,5 0,069

700·0,296

β₃= ———— = 10,32 см/ч

20

По полученным значениям β рассчитаем толщину диффузионного слоя δ

D D δ₁ 10,32

δ₁ = —— и δ₃ = ——; —— = ——— = 0,56

β₁ β₃ δ₃ 18,27

Толщина диффузионного слоя при изменении числа оборотов уменьшилась почти в двое.

3.1.9. Над углем пропускают воздух при Р = const. В результате протекает реакция С + О₂ = С0₂. Эффективную константу k*

определили при различных температурах. Результаты измерений и вычислений:

T, K…777 873 973 1073 1173 1273 1373 1673 (1/T)·10³..1,290 1,145 1,026 0,930 0,85 0,785 0,728 0,636

k* …0,073 0,447 2,15 6,81 13,72 19,49 24,40 26,90

lg k*.-1,137 -0,35 0,332 0,832 1,137 1,29 1,369 1,429

Составьте уравнение типа

 

lgk = A/T+const.

Решение. Сопоставив уравнение lgk = AIT + const с уравнением, получим

 

Е —25,47·10³

А _=- — = —————— = 1 33- Ю³.

2,3 R 2,3·8,31

Для вычисления const подставляем в исследуемое уравнение значения lg k и 1/Т, относящиеся к кинетической области протекания реакции для 973 К:

0,332=—1,33· 10³/973+ const,

откуда const = 0,244. После подстановки чисел получим

lg k = 0,244 — 5573/T.

3.1.10. При исследовании кинетики реакции бромирования серебра Ag + VaBra = AgBr получены следующие данные (500 К, Рвг,= .— 170 мм рт. ст.):

t,c……………….. 1000 2000 3000 4000 6000

(∆m/S)·10², г/см².. 1 1,34 1,61 1,84 2,24

(∆m/S)²·10⁴, г/см⁴.. 1 1,8 2,6 3,4 5_

Какие выводы о типе реакции можно сделать на основании результатов опыта? Вычислите константу скорости реакции.

Решение. Поскольку на металлическом серебре в ходе реакции образуется бромид серебра, можно предположить, что скорость реакции лимитируется скоростью диффузии Ag или Br через слой AgBr. Для проверки предположения строим графики зависимостей Am/S == ƒ(t)(1) и (∆m/S)². = ƒ(t) (2). Прямая в координатах (∆m/S)² — t подтверждает предположение о том, что реакция протекает в диффузионной области. Константу скорости k* находим из графика как тангенс угла наклона прямой:

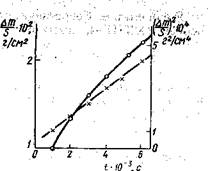tgα = k = 8,0·10-⁸ г²/(см⁴с).