Великая теорема Ферма формулируется следующим образом: диофантово уравнение:
Аn+ Вn = Сn (1)
где n - целое положительное число, большее двух, не имеет решения в целых положительных числах.
Суть Великой теоремы Ферма не изменится, если уравнение (1) запишем следующим образом:
Аn = Сn - Вn (2)
Пусть показатель степени n=4. Тогда уравнение (2) запишется следующим образом:
А4 = С4 -В4 (3)
Уравнение (3) запишем в следующем виде:
А4 = (С2) 2 - (В2)2 = (С2 -В2) ∙ (С2 +В2) (4)
Пусть: (С2 -В2) = N4 (5)
Уравнение (5) рассматриваем как параметрическое уравнение 4 - ой степени с параметром N и переменными B и С. Преобразуем уравнение (5):
N4 = (С -В) · (С +В) (6)
Для доказательства используем метод замены переменных. Обозначим:
C-B=M (7)
Из уравнения (7) имеем:
C=B+M (8)
Из уравнений (6), (7) и (8) имеем:
N4=M∙ (B+M+B) =M∙ (2B+M) = 2B∙M+M2 (9)
Из уравнения (9) имеем:
N4 - M2= 2B∙M (10)
Отсюда:
B =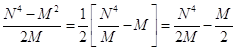 (11)
(11)
Из уравнений (8) и (11) имеем:
C= 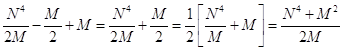 (12)
(12)
Из уравнений (11) и (12) следует, что необходимым условием для того чтобы числа В и С были целыми, является делимость числа N4 на число M, т.е. число M должно быть одним из сомножителей, входящих в состав сомножителей числа N4.
Из уравнений (11) и (12) также следует, что необходимым условием для того чтобы числа В и С были целыми, является также одинаковая четность чисел N и M: оба числа должны быть четными или оба нечетными.
Из уравнений (11) и (12) также следует:
С2 +В2= 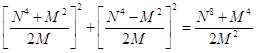 (13)
(13)
Обозначим:
С2 +В2 = K (14)
Пусть:
N=P∙S; M=S2
Тогда:
K = С2 +В2 = 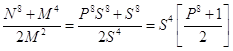 (15)
(15)
Из уравнений (4), (5) и (15) следует:
A4 = N4∙ K=N4· S4∙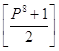 (16)
(16)
Отсюда следует:
A = N· S∙![]() (17)
(17)
Очевидно, что:
![]() - дробное число.
- дробное число.
То есть:
С2 + В2 ≠ R4; A4 ≠ N4∙R4
Следовательно, в соответствии с формулой (17) число А - дробное число.
Другими словами, определенные по формулам (11) и (12) значения чисел B и С удовлетворяют только уравнению (5) и не удовлетворяют предполагаемому равенству:
С2 + В2 = R4
Таким образом, великая теорема Ферма не имеет решения в целых положительных числах для показателя степени n=4.
Похожие работы
оложительное число, большее двух, не имеет решения в целых положительных числах. Суть Великой теоремы Ферма не изменится, если уравнение /1/ запишем следующим образом: Аn = Сn - Вn (2) Рассмотрим частное решение уравнения (2) при показателе степени n=3. В этом случае уравнение (2) запишется следующим образом: A3 = C3 - B3 = (C-B) ∙ (C2 + C·B +B2) (3) Обозначим: C - B = K (4) ...
... , но теоремы, полные доказательства которых, как утверждал Ферма, у него имелись, все впоследствии были доказаны (основной вклад в доказательство которых внёс Эйлер). Но было и одно исключение – приятное исключение – это Великая теорема Ферма: История Большой теоремы Ферма Большой известностью во всём мире пользуется «Великая теорема Ферма» (она же – «Большая» или «Последняя»). ...
... спортивный или престижный характер. Вопреки мнению ученых математиков, ниже предлагается к обсуждению официальным лицам из института им. В.А. Стеклова и любителям математики из Интернета компактный, практически на 2-х страницах способ элементарного доказательства теоремы Ферма в общем виде, основанный на разложении уравнений Ферма по биному Ньютона на его составляющие. Это позволяет после ...
... n = q ³ 3 и четном значении z также не имеет целочисленных решений. Поэтому далее достаточно доказать, что целочисленных решений не имеет также и уравнение (14). Доказательство великой теоремы ферма. Уравнения (1) и (14) полностью эквивалентны, т.е. либо не существует целочисленных решений у обоих уравнений, либо целочисленные решения одновременно имеют уравнения (1) и (14). Покажем, что ...
0 комментариев