Записать задачу двойственную к данной, решить одну из пары задач и отыскать оптимальное решение второй

Министерство образования и науки Украины

Днепропетровский Национальный Университет

Факультет электроники, телекоммуникаций и компьютерных систем

Кафедра АСОИ

Расчётная задача №4

«Исследование операций»

г. Днепропетровск

2007г.

Задача

Записать задачу двойственную к данной, решить одну из пары задач и отыскать оптимальное решение второй

Прямая задача имеет вид:

Общая постановка двойственной задачи

Двойственная задача – это вспомогательная задача линейного программирования, она формулируется из прямой задачи.

Идея метода основана на связи между решениями прямой и двойственной задачи.

Двойственная задача формируется непосредственно из условий прямой задачи за следующими правилами:

Если прямая задача является задачей максимизации, то двойственная будет задачей минимизации;

Коэффициенты целевой функции прямой задачи С1, С2, ….,Сn становятся свободными членами ограничений двойственной задачи;

Свободные члены ограничений прямой задачи b1, b2, ….,bn становятся коэффициентами целевой функции двойственной задачи;

Матрицу ограничений двойственной задачи получают транспонированием матрицы ограничений прямой задачи;

Если прямая задача является задачей максимизации, то во всех неравенствах двойственной задачи будут стоять знаки ≥, и знаки ≤, если прямая задача является задачей минимизации.

Число ограничений прямой задачи равно числу переменных двойственной задачи.

Прямая задача в канонической форме

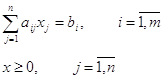
Двойственная к ней задача будет иметь вид

Двойственная задача решается симплекс-методом до достижения оптимального решения.

Решение прямой задачи

Все ограничения прямой задачи - это равенства с неотрицательными правыми частями, когда все переменные неотрицательны.

Приведем прямую задачу к стандартному виду:

 

Подставим значение  в целевую функцию:

 

Таким образом, прямая задача в стандартной форме имеет следующий вид:

Строим симплекс таблицу:

Итерация №1

Базис							Решение	Оценка
			0	0		0
	5	-2	1	0	0	0	4	-
	-1	2	0	1	0	0	4	2
	1	1	0	0	-1	1	4	4

 - ведущий столбец

 - ведущая строка

Итерация №2

Базис							Решение	Оценка
		0	0			0
	4	0	1	1	0	0	8	2
		1	0		0	0	2	-
		0	0		-1	1	2

- ведущий столбец

- ведущая строка

Итерация №3

Базис							Решение	Оценка
	0	0	0
	0	0	1
	0	1	0					-
	1	0	0					-

- ведущий столбец

- ведущая строка

Итерация №4

Базис							Решение
	0	0			0		8
	0	0			1	-1	1
	0	1			0	0	3
	1	0			0	0	2

Оптимальное решение прямой задачи:

, Х = {2 , 3}

Решение двойственной задачи

Двойственная задача имеет вид:

 

 

 

 

 

   

   

     

 

Мы получили двойственную задачу и будем решать ее М-методом. Приведем систему линейных неравенств к стандартному виду, перед этим сделав замену:

,

,

 

  

 

 

Подставим значения  в функцию:

  

Таким образом, двойственная задача в стандартной форме имеет следующий вид:

Симплекс-таблица, итерация 1

Базис										Решение	Оценка
								0	0
	-5	5	1	-1	-1	-1	0	1	0	1
	2	-2	-2	2	-1	0	-1	0	1	2	-

- ведущий столбец

- ведущая строка

Симплекс-таблица, итерация 2

Базис										Решение	Оценка
	0	0							0
	-1	1					0		0		-
	0	0					-1		1

- ведущий столбец

- ведущая строка

Симплекс-таблица, итерация 3

Базис										Решение
	0	0	1	0	1	2	3			-8
	1	1	0	0
	0	0	-1	1

  

  

Оптимальное решение двойственной задачи:

, , ,

Ответ

Оптимальное решение прямой задачи:  , X = { 2 , 3 }

Для двойственной задачи: , , ,