Введение
С небольшими числами иметь дело очень просто: наборы из трех-четырех предметов легко узнать «в лицо», так что считать их нет необходимости. Но как, к примеру, выяснить, не потерялась ли овца из большого стада? Здесь уже не обойтись без подсчета. Чтобы пересчитать стадо, проще всего использовать камешки: один камешек – один объект, в данном случае овца.
Считать при помощи камешков удобно и просто, если объектов немного. С большими числами уже сложнее: и нужного количества камешков можно не набрать, и поднять такой мешок не каждому под силу. В некоторых сообществах для счета использовались пальцы рук и ног, но все равно оставалась проблема с числами больше 20… [№3.1, стр. 343]
Значение цифр и чисел в нашей жизни трудно переоценить. Биологи утверждают, что в составе человеческого мозга есть структуры (кора левого полушария у правшей), отвечающие за формирование устной и письменной речи. Таких структур нет ни у одного другого животного. Благодаря им человек может писать, читать, говорить, произносить самые разнообразные звуки. Именно из-за такого сложного строения головного мозга человек смог в первый раз произнести слово, написать букву. Теперь мы не можем себе представить жизни без алфавита и слов.
В математике таким алфавитом являются цифры, а словами – числа. Есть много общего: своеобразными языками в математике являются системы счисления. В таких алфавитах буквы – цифры. Чаще всего математический язык легче языка лингвистического, прежде всего объемом информации, которую несет один символ.
Изобретение десятичной системы счисления относится к главным достижениям человеческой мысли. Без нее вряд ли могла существовать, а тем более возникнуть современная техника и наука вообще.
Глава 1. История цифр. Числа и счисление.
§ 1 На заре появления цифр.
Давно, очень давно это было. Человек сидел у водопоя, спрятавшись в кустах, и ждал зверя. К воде подошел олень с большими ветвистыми рогами. Охотник загнул на руке палец. Затем к водопою вышел безрогий олень. Охотник загнул еще один палец. Всю ночь просидел в засаде охотник, но больше ни одного зверя не увидел. Утром он рассказывал старшему соплеменнику о своих наблюдениях:
— Сижу, смотрю, вышел к водопою рогатый олень (охотник для подтверждения положил на ладонь угловатый камешек), а затем вышел безрогий олень (положил рядом с первым овальный камешек). Больше зверей не было до утра.
— Так к водопою сначала подошел один олень, а затем еще один? — переспросил родич и поднял два пальца.
— Да, — ответил охотник.
К следующей ночи старший собрал большую группу мужчин с копьями. Он тщательно продумал, куда посадить одного охотника, куда — двух, а куда и трех. Все были размещены у водопоя так, чтобы подошедший олень попал в окружение. Охота была удачной.
Этот случай показывает, что уже на заре развития человеческого общества люди замечали, что различные группы предметов — звери, охотники, камни — могут иметь одно и то же число: два пальца, два зверя, два камня и т. д. В наши дни об этом знает любой первоклассник. Если разложить напротив друг друга, например, кружки и палочки, нетрудно убедиться, что кружков окажется столько же, сколько палочек. Этим мы устанавливаем взаимно-однозначное соответствие. Так и первобытные люди, сопоставляя одну группу (множество) предметов с другой (другим множеством), видели сходство и различие обеих групп (множеств).
В то далекое время понимание того, что одна группа (множество) может быть похожа на другую (множество), стало для человека громадным продвижением в его развитии. Это было величайшим открытием. Оно помогло людям научиться видеть взаимно-однозначное соответствие предметов двух множеств, а затем и считать эти предметы.
Постепенное совершенствование жизненного уклада первобытных людей способствовало возникновению у них потребности считать, но прошли десятки столетий, прежде чем люди приобрели это умение.
Вначале человек научился выделять единичные предметы. Например, из стаи волков, стада оленей он выделял одного вожака, из выводка птенцов — одного птенца и т. д Научившись выделять один предмет из множества других, говорили: «один», а если их было больше — «много» Даже для названия числа «один» часто пользовались словом, которым обозначался единичный предмет, например: «луна», «солнце». Такое совпадение названия предмета и числа сохранилось в языке некоторых народов до наших дней.
Частые наблюдения множеств, состоящих из пары предметов (глаза, уши, крылья, руки), привели человека к представлению о числе два. До сих пор слово «два» на некоторых языках звучит так же, как «глаза» или «крылья».
В некоторых племенах Австралии долгое время пользовались только числами «один» и «два», а все другие называли, повторяя эти числа или говоря «много».
В одном из австралийских племен считали иначе. Один называли «мал», два — «булан», три — «гулиба», т. е. названия имели только три первых числа, а другие числа, например 4, называли «булан-булан» и т. д. Эти исторические факты показывают, как люди учились считать. Так как в далекие времена общение между разными народами было затруднено, то способы счета и названия чисел в разных местах одной страны были неодинаковы. [№2, cтр. 11-13]
С появлением городов и каменных сооружений все больше людей стали заниматься письменностью и началами математики. Самые сведущие придумали специальные знаки для записи чисел. Эти знаки, выполняющие роль цифр, были удобны для чтения, но для их записи требовалось довольно много времени.
Первый способ обозначения чисел, приходящий на ум, - палочками. Что может быть легче? Одна палочка значит один, две – два и так далее. Вот одна интересная история о такой нумерации.
В марте 1917 г. жители Ленинграда (тогда — Петрограда) были не мало озадачены и даже встревожены таинственными знаками, появившимися, неизвестно как, у дверей многих квартир. Молва приписывала этим знакам разнообразные значения. Они имели форму черточек, чередующихся с крестами.
Пошли зловещие слухи о грабительских шайках, помечающих квартиры будущих жертв. «Комиссар временного правительства по г. Петрограду», успокаивая население, утверждал, что «таинственные знаки, которые чьей-то невидимой рукой делаются на дверях мирных обывателей в виде крестов, букв, фигур, как выяснилось по произведенному дознанию, делаются провокаторами и германскими шпионами»; он приглашал жителей эти знаки стирать и уничтожать, «а в случае обнаружения лиц, занимающихся этой работой, задерживать и направлять по назначению».
Подобные знаки замечены во многих домах на черных лестницах у дверей квартир. Обычно знаки этого типа имеются у всех хводных дверей данного дома, причем в пределах одного дома двух одинаковых знаков не наблюдается. Их мрачное начертание, естественно, внушаеат тревогу жильцам. Между тем, смысл их легко раскрывается, если сопоставить их с номерами соответствующих квартир. Нетрудно теперь догадаться, что кресты означают десятки, а палочки – единицы; так оказалось во всех без исключения случаях. Эта своеобразная нумерация, очевидно, принадлежит дворникам-китайцам, не понимавшим наших цифр. [№1, стр. 9-11]
§2 Старинные способы нумерации.
Более сложный способ обозначения чисел был придуман римлянами. Они записывали числа черточкми, и времени для этого требовалось меньше. Ученые предполагают, что римская пятерка – это упрощенное изображение руки с пятью растопыренными пальцами, а десять – это две сложенные вместе пятерни.
В старину на Руси цифры обозначались буквами. Для указания того, что знак является не буквой, а цифрой, сверху над ним ставился специальный знак « ~ », называемый «титло» (см. рис.). Тысячи обозначались теми же буквами с «титлами», что и первые девять цифр, но у них слева внизу ставился специальный знак. Десятки тысяч назывались «тьмы», и их обозначали, обводя знаки единиц кружками . Отсюда произошло выражение «Тьма народу», т.е. очень много народу. Сотни тысяч назывались «легионами» («легеонами»), их обозначали, обводя знаки единиц кружками из точек. Миллионы назывались «леодрами». Их обозначали, обводя знаки единиц кружками из лучей или запятых. Десятки миллионов назывались «воронами» или «вранами», и их обозначали, обводя знаки единиц кружками их крестиков или ставя по обе стороны буквы букву К. Сотни миллионов назывались «колодами». «Колода» имела специальное обозначение: над буквой и под ней ставили квадратные скобки. Остальные числа записывались буквами слева направо. При записи больших чисел, чем тысячи, в практической деятельности часто вместо кружков знак, обозначающий тысячу, ставили перед буквами, обозначавшими десятки и сотни. В приведенной системе обозначения чисел не шли дальше тысяч миллионов. Такой счет назывался «малый счет». В некоторых рукописях авторами рассматривался и «великий счет», доходивший до числа 1050. Далее говорилось: «И более сего несть человеческому уму разумети». [№4, стр. 135-137]
В источнике №2 сообщается, что тьмой называли 106, легеоном – 1012, леодром – 1024, вороном – 1048, а колодой, самым большим числом великого счета, - 1049. В том, что дальше 1050 счет не велся оба источника согласны.
Сходная нумерация существовала у греков.Для нумерации чисел греческие математики придумали алфавитную нумерацию. Первая буква их алфавита – альфа обозначала 1, вторая – бета – 2 и т. д.
В дореволюционное время на вещах, купленных у офеней или в частных магазинах, особенно провинциальных, можно было зачастую заметить непонятные буквенные обозначения вроде
а ве в уо.
Это не что иное, как цена вещи без запроса, которую торговец обозначал на товаре, но так, однако, чтобы ее не мог разгадать покупатель. Бросив взгляд на эти буквы, торговец сразу проникал в их скрытый смысл и, сделав надбавку, называл покупателю цену с запросом.
Система обозначений была весьма проста. Торговец выбирал какое-нибудь слово, составленное из 10 различных букв; чаще всего останавливали выбор на словах: трудолюбие, правосудие, ярославецъ, миролюбецъ, Миралюбовъ. Первая буква слова обозначала—1, вторая — 2, третья — 3 и т д; десятою буквою обозначался ноль С помощью этих условных букв-цифр торговец обозначал на товарах их цену, храня в строгом секрете «ключ» к своей системе прибылей.
Если например, выбрано было слово
правосудие
1234567890
то цена 4 р 75 к. обозначалась так:
в уо.
Иногда цена на товаре писалась в виде дроби, например:
![]() ое
ое
тро
Это значит при ключе «трудолюбие», что надо запросить 1 р. 25 к., себе же книга стоила 50 коп. [№1, стр. 13-14]
«Нумерация» в то время давно уже была в широком употреблении и понятна была каждому, даже неграмотному крестьянину. Восходит она, без сомнения, к глубокой древности и употребительна была не только у нас. Такая нумерация называется «народной».
Любопытно, что эта народная нумерация была некогда у нас даже узаконена: по такой именно системе, только более развитой, должны были вестись сборщиками податей записи в податной тетради. «Сборщик, — читаем мы в старом «Своде законов», — принимая от кого-либо из домохозяев вносимые к нему деньги, должен сам, или через писаря, за-писать в податной тетради против имени того домохозяина, которого числа сколько получено денег, выставляя количество принятой суммы цифрами и знаками. Знаки сии для сведения всех и каждого ввести повсеместно одинаковые, а именно:
В другом месте того же тома «Свода законов» находим еще раз упоминание об обязательном употреблении народных числовых обозначений. Приводятся особые знаки для тысячи рублей—в виде шестиконечной
звезды с крестом в ней, и для ста рублей — в виде колеса с 8 спицами. Но обозначения для рубля и десяти копеек здесь устанавливаются иные, чем в предыдущем законе.
Вот текст закона об этих так называемых «ясачных знаках»:
«Чтобы на каждой квитанции, выдаваемой Родовитому Старосте, от которого внесен будет ясак, кроме изложения словами, было показываемо особыми знаками число внесенных рублей и копеек так, чтобы сдающие простым счетом сего числа могли быть уверены в справедливости показания *. Употребляемые в квитанции знаки означают: (звезда) тысяча рублей, (колесо) сто рублей, (квадрат) десять рублей, X один рубль, ||||| |||| десять коп., | копейку.
«Дабы не можно было сделать здесь никаких прибавлений, все таковые знаки очерчивать кругом прямыми линиями». Например, 1232 р. 24 к. изображают так, как показано на рисунке. [№1, стр. 11-13]
Как видите, употребляемые нами арабские и римские цифры — не единственный способ обозначения чисел. В старину применялись у нас, да еще и теперь кое-где по деревням применяются другие системы письменного счисления, отдаленно сходные с римскими и совсем не сходные с арабскими цифрами.
§3 Системы счисления.
Как уже было сказано, в некоторых сообществах для счета использовались пальцы рук, однако этот способ годился только в пределах 10. Кое-где прогресс пошел дальше: к счету приобщали и пальцы ног, но все равно оставалась проблема с числами больше 20.
Выход нашелся: считать на пальцах до 10, а затем начинать сначала, отдельно подсчитывая количество десятков. Система счисления на основе десяти возникла как естественное развитие пальцевого счета. Существовало, однако, несколько отклонений от этой системы. Например, 4000 лет назад жители Древнего Вавилона использовали систему счета до 60. Следы шестидесятеричной системы в наше время сохранились в делении часа и углового градуса на 60 минут, а минуты - на 60 секунд.
По мере развития речи люди начали использовать слова для обозначения чисел. Отпала необходимость показывать кому-то пальцы, камешки или реальные предме-ш, чтобы назвать их количество. Для изображения чисел стали применяться рисунки, чертежи или символы. Например, для ответа на вопрос «Сколько овец в стаде?» достаточно нарисовать или начертить группу животных. Но считать можно гораздо быстрее, применяя для обозначения чисел какие-либо символы. Египтяне для чисел до 9 использовали последовательности простых штрихов и специальный символ - для 10. Вавилоняне имели аналогичную систему, а римляне ввели новый символ при достижении 5. Существовали и системы с отдельными символами для каждой цифры до 9 включительно, как в арабской системе счисления, которую мы сейчас используем, а у греков имелся специальный символ и для 10. [№3.1, стр. 343-344]
Появилась десятичная система, вероятно, в Индии. Выбор графических изображений для цифр, разумеется, не принципиален. Современные изображения цифр – простая стилизация древних арабских цифр. Марокканский историк Абделькари Боужибар считает, что арабским цифрам в их первоначальном варианте было придано значение в строгом соответствии с числом углов, которые образуют фигуры.
В десятичной системе каждая цифра несет двойную информацию: свое собственное значение и место, которое она занимает в записи числа (разряд). Такие системы счисления называются позиционными. Римскую систему счисления можно скорее назвать аддитивной, поскольку чосло образуется при сложении и вычитании значений специальных значков. В аддитивных системах счисления выполнять арифметические действия безнадежно – неудивительно, что такие системы не прижились. [№5, стр.33-34]
Вот запись из дневника одного математика:
«Я окончил курс университета 44 лет от роду. Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте – всего 11 лет – способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья из 10 детей. Жалования я получал в месяц всего 200 рублей, из которых 1/10 мне приходилось отдавать сестре, так что мы с детьми жили на 130 руб. в месяц» и т. д.
На первый взгляд странная биография, но только на первый. Разберемся в чем тут дело.
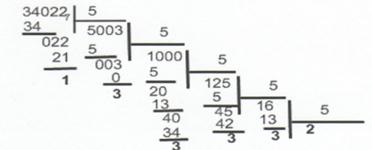
А все дело в том, что отрывок написан с использованием недесятеричной системы счисления, такой привычной для большинства людей. Можно легко догадаться, какую именно систему использовал автор. Секрет выдается фразой: «Спустя год (полсе 44 лет), 100-летним молодым человеком…» Если в от прибавления одной единицы число 44 преображается в 100, значит цифра 4 – наибольшая в этой системе счисления, т. е. основанием системы является 5. Немного сложнее перевести остальные числа в «родную» десятичную. Например, несложно догадаться, что одна единица третьего разряда равна 5 во второй степени, т. е. 25 (так же в десятичной системе одна единица третьего разряда равна 100, т. е. 102). А единица второго разряда равна 51, третьего – 50. Теперь несложно восстановить реальную биографию чудака-автора.
При желании можно создать собственную биографию в таком же роде. Скажем, вам 17 лет. Воспользуемся для записи возраста четвертичной системой счисления. Разделим 17 на 4:
17 : 4 = 4, остаток 1
Остаток – это и есть число единиц первого разряда. Результат целочисленного деления снова поделим на 4:
4 : 4 = 1, остаток 0
Теперь остаток – число единиц второго разряда. Ну а последнее частное – единицы третьего разряда. Теперь составим из наших ответов число. Получили 101, т. е. 1710=1014.
Помеха может возникнуть вследствие того, что в некоторых случаях не будет доставать обозначений цифр. При изображении чисел в системах с основаниями больше 10 может явиться надобность в цифрах «десять», «одиннадцать» и т. д. [№1, стр. 56-57]
Обычно для обозначения их применяют латинский алфавит: «десять» обозначают буквой «А», «одиннадцать» - буквой «В». Когда буквы заканчиваются, ничего не поделаешь – придется обозначать двумя, тремя буквами сразу, да еще и обводить, скажем, кружочком, чтобы было видно, что это цифра, а не двузначное число.
Нетрудно производить арифметические действия в разных системах счисления. Только надо помнить, что переходить через разряд надо, когда цифра превышает максимально допустимую в данной системе. Легко догадаться, что для любой системы такая цифра на единицу меньше основания. Заметим, что в самой «маленькой» из систем – двоичной – выполнять разнообразные арифметические действия с точки зрения умственной нагрузки легче всего, хотя для этого понадобится много времени и бумаги (если считать столбиком). Ну а в целом это дело привычки.
Легко доказать, что в любой системе счисления выполняются такие положения (если в системе имеются соответствующие цифры):
121 : 11 = 11
144 : 12 = 12
21 • 21 = 441. [№1, стр. 67]
Глава 2. Способы запоминания чисел.
§ 1 Различные приспособления для запоминания чисел.
Вероятно, самый древний способ запоминания чисел – камешками. Сколько камешков – столько предметов надо запомнить. Когда камешков не стало хватать, человек придумал разрядность (системы счисления). Число в таком виде записать легче, например, при помощи узелков. Так делали древние перуанцы, завязывая узелки на нескольких сплетенных вместе веревках. Такой «прибор» назывался «квипос». Он был в принципе эквивалентен нашим счетам и ,без сомнения, связанный с ними общностью происхождения. На таких счетах однократно завязанный узел означал 10, двукратно – 100 и т. д. Однако пользоваться таким прибором нелегко: на завязывание – перевязывание узелков уходит много времени. Выход нашелся – сделать систему подвижной.
Древние народы — египтяне, греки, римляне — употребляли при вычислениях счетный прибор «абак». Это была доска (стол), разграфленная на полосы, по которым передвигали особые шашки, игравшие роль косточек наших счетов Такой вид имел греческий абак Абак римский имел форму медной доски с желобами (прорезами), в которых передвигались кнопки. Родственен абаку перуанский «квипос» — ряд ремней или бечевок с завязанными на них узлами этот счетный прибор получит особенное распространение среди первых обитателей Южной Америки, но, без сомнения, был в употреблении также и в Европе. В средине века, вплоть до XVI века, подобные приспособления были широко распространены в Европе. Но теперь видоизмененный абак — счеты — сохранился, кажется, только у нас, да в Китае (семикосгочковые счеты — «суан-пан» *) и Японии (тоже семикосточковые счеты — «соробан»). Каждый грамотный человек умеет там выполнять на таких счетах четыре арифметических действия Между тем Запад почти не знает счетов, — вы не найдете их ни в одном магазине Европы, и только в начальных школах имеются огромные счеты — наглядное классное пособие при обучении нумерации. Быть может, потому-то мы и не ценим этого счетного прибора так высоко, как он заслуживает, а смотрим на него как на наивную кустарную самодельщину в области счетных приборов Японцы ценят свои счеты высоко. Вот как отзывается о соробане один японский ученый «Несмотря на свою древность, соробан превосходит все современные счетные приборы легкостью обращения с ним, простотою устройства и дешевизною»
Мы тоже вправе были бы гордиться нашими конторскими счетами, так как при изумительной простоте устройства они по достигаемым на них результатам могут соперничать в некоторых отношениях даже со сложными, дорого стоящими счетными машинами. [№1, стр.34-36, 39-40]
Об арифметических действиях на счетах будет написано в главе 3.
§2 Современные способы запоминания чисел.
Самая простая система счисления – двоичная, так как она использует только две цифры: ноль и один. Именно такую систему счисления используют современные компьютеры. В основном из-за того, что такой «язык» легок для «понимания» электронных устройств: наличие электрического сигнала означает единицу, его отсутствие – ноль. А дальше открываются поистине безграничные возможности для запоминания самой разной информации – ведь любой ее вид, будь то текст, изображение, звук или видео, можно представить в виде набора чисел. Ввели даже единицу информации: информация, говорящая об одном из 256 равновероятных событий, имеет объем в один байт.
Информацию в виде двоичного кода можно размещать на разнообразных носителях. Например, на гибких магнитных лентах – в виде намагниченных и ненамагниченных областей, на поверхности лазерного диска – в виде углублений (питов) и выступов, в интегральных микросхемах – сложным сочетанием полупроводниковых приборов, выполненным на единой подложке из диэлектрика.
В настоящее время разобрав калькулятор, не увидите там ничего из электроники, кроме маленькой интегральной микросхемы, залитой небольшой каплей эпоксидной смолы. Это наглядно иллюстрирует тот факт, что будущее современной техники в ее миниатюрности. Такой прибор починить не представляется возможным:узор из тысяч плоских транзисторов величиной в доли микрона невозможно изменить лучшему специалисту. Так и делают современные микросхемы, защищая их раз и навсегда прочной оболочкой.
Такая сложность вычислительной техники является результатом многовекового развития. Перфокарты (картонные карточки в отверстиями) впервые были применены в 1787 г., когда французский ткач Робер Фалькон использовал их для управления механическим ткацким станком. Позже эта система была усовершенствована другим ткачем, Жозефом Жаккаром. Ряды отверстий (перфорация) в наборе карт использовались для хранения деталей узора. При замене карточек ткацкий станок ткал другой узор.
«Жаккардовый станок выполнит любой узор, который в состоянии представить себе воображение», - говорил англицский математик Чарльз Бэббидж. Его настолько потрясло разнообразие, которое давали перфокарты, что в 1832 г. он начал проектировать то, что назвал «аналитической машиной», однако, в то время построить такой механизм было невозможно из-за его сложности. Но с этого началась эра электронной информации. [№3.2, стр. 99-100]
Принцип работы перфокарт весьма прост: в том месте, где в карте проделано отверстие, могут соприкасаться два электрода, и через них потечет ток. Понятно, что ток при относительно малом напряжении не сможет пробить картонную карту – сигнала не будет. Получается, что перфокарта тоже использовала двоичный код для записи информации в позиционной системе счисления – каждое отверстие или его отсутствие несут двоякую информацию – о своем местоположении и об одном из двух фактов – есть дырка или же ее нет.
§3 Память на числа.
Поразительная сила образов (или эйдосов, как их называли древние греки) была известна человечеству с древнейших времен. В настоящее время эйдетизм рассматривается как разновидность образной памяти, выраженной в сохранении ярких, наглядных образов предметов. Обладающий эйдетизмом человек не воспроизводит в памяти воспринимавшиеся им предметы, а продолжает как бы видеть их.
У разных лиц бывает и различная память по отношению к числам, годам, ценам; различие это зависит от неодинаковой степени развития математических способностей. Лицо, широко развившее эти способности, будет неизменно сохранять ясное и прямое впечатление о числах и обо всем, связанном с ними, тогда как лицо со слабо развитыми способностями найдет затруднительным помнить что-либо подобное, даже усиленно занимаясь умственными вычислениями, но последние, однако, могут развить эту способность. [№6, В.В.Аткинсон]
Есть, по моему мнению, различие между запоминанием, скажем, дат, цен и формул, получившихся при решении арифметических задач. Несмотря на то, что во всех трех случаях объектом запоминания служит число, некоторым людям довольно сложно сопоставить несколько запомненных дат или цен с определенными событиями или товарами. В то же время этот человек может безошибочно рассказать все подробности своих вычислений на недавней контрольной работе по математике. Здесь, на мой взгляд, весьма существенным фактором является заинтересованность лица в запоминании числа. Если историю учить неинтересно, то и даты не смогут уложиться в мозгу. Хотя я соглашаюсь с В. Аткинсоном в том, что память можно развивать, считаю, что при крайней незаинтересованностью предметом это сделать весьма сложно.
Числа могут объединяться со всяким предметом, с которым они естественно связаны. Но если такой подходящий предмет, с которым можно было бы связать число, отсутствует, то нужно ограничиться лишь способом "простого созерцания". Этот способ состоит в том, что данное число фотографируется в уме, пока последний не воспроизведет все детали и вид числа, как детали и общий вид какой-нибудь картины. Вам следует представить себе числа, написанные жирным белым шрифтом на черном поле. Не упускайте умственной картины, пока вы не будете полностью видеть ее своим мысленным взором. Искусство это возрастает с практикой. Но, однако, было бы лучше связывать числа с какими-нибудь подходящими предметами. Теория такого "созерцательного" способа со связыванием или без него основана на том факте, во-первых, что многие умы воспринимают и удерживают зрительные впечатления гораздо скорее и лучше, чем простую абстрактную идею без конкретного изображения, и, во-вторых, что закон ассоциации дает умственной картине с большим числом возможностей легко возвращаться в поле сознания, когда эту картину затребует мысль о предмете. . [№6, В.В.Аткинсон, стр. 436]
Глава 3. Счисление.
§ 1 Умножение и деление на счетах.
Есть много полезных вещей, которые мы не ценим только потому, что, находясь постоянно у нас под руками, они превратились в слишком обыденный предмет домашнего обихода. К числу таких недостаточно ценимых вещей принадлежат и наши конторские счеты — русская народная счетная машина, представляющая собою видоизменение знаменитого «абака» или «счетной доски» наших отдаленных предков.
Наверное, очень многие умеют складывать, вычитать и делить на два на счетах.
Вот несколько приемов, (пользуясь которыми, всякий умеющий быстро складывать на счетах сможет проворно выполнять встречающиеся на практике примеры умножения.
Умножение на 2 и на 3 заменяется двукратным и троекратным сложением.
При умножении на 4 умножают сначала на 2 и складывают этот результат с самим собой.
Умножение числа на 5 выполняется на счетах так: переносят все число одной проволокой выше, то есть умножают его на 10, а затем делят это 10-кратное число пополам (как делить на 2 помощью счетов — мы уже объяснили выше, на стр. 33).
Вместо умножения на 6 умножают на 5 и прибавляют умножаемое. Вместо умножения на 7, множат на 10 и отнимают умножаемое три раза.
Умножение «а 8 заменяют умножением на 10 минус два.
Точно так же множат на 9: заменяют умножением на 10 минус один.
При умножении на 10 переносят, как мы уже сказали, все число одной проволокой выше.
Читатель, вероятно, уже сам сообразит, как надо поступать при умножении на числа, больше 10, и какого рода замены тут окажутся наиболее удобными. Множитель 11 надо, конечно, заменить 10 + 1. Множитель 12 заменяют 10 + 2, или практически 2+10, т. е. сначала откладывают удвоенное число, а затем прибавляют удесятеренное. Множитель 13 заменяется 10 + 3 и т. д.
Легко видеть, между прочим, что с помощью счетов очень удобно умножать на такие числа, как на 22, 33, 44, 55 и т. п.; поэтому надо стремиться при разбивке множителей пользоваться подобными числами с одинаковыми цифрами.
К сходным приемам прибегают и при умножении на числа, больше 100. Если подобные искусственные приемы утомительны, мы всегда, конечно, можем умножить с помощью счетов по общему правилу, умножая каждую цифру множителя и записывая частные произведения — это все же дает некоторое сокращение времени,
Выполнять с помощью конторских счетов деление гораздо труднее, чем умножать: для этого нужно запомнить целый ряд особых приемов, подчас довольно замысловатых.
Делить на 2 очень просто.
Гораздо сложнее прием деления на 3: он состоит в замене деления умножением на бесконечную периодическую дробь 0,333... (известно, что 0,333.. = ![]() ) Умножать с помощью счетов на 3 мы умеем; уменьшить в 10 раз тоже несложно: надо лишь переносить делимое одной проволокой ниже. После недолгого упражнения этот прием деления на 3, на первый взгляд длинноватый, оказывается довольно удобным на практике.
) Умножать с помощью счетов на 3 мы умеем; уменьшить в 10 раз тоже несложно: надо лишь переносить делимое одной проволокой ниже. После недолгого упражнения этот прием деления на 3, на первый взгляд длинноватый, оказывается довольно удобным на практике.
Деление на 4, конечно, заменяется двукратным делением на 2.
Еще проще деление на 5: его заменяют делением на 10 и удвоением результата.
На 6 делят в два приема: сначала делят на 2, потом полученное делят на 3.
Деление на 7 выполняется с помощью счетов чересчур сложно, и потому здесь излагать его не буду.
На 8 делят в три приема: сначала на 2, потом полученное вновь на 2 и затем еще раз на 2.
Очень интересен прием деления на 9. Он основан на том, что ![]() = 0,1111 ... Отсюда ясно, что вместо деления на 9 можно последовательно складывать 0,1 делимого + 0,01 его и т. д.
= 0,1111 ... Отсюда ясно, что вместо деления на 9 можно последовательно складывать 0,1 делимого + 0,01 его и т. д.
Всего проще, как видим, делить на 2, 10 и 5 и, конечно, на такие кратные им числа, как 4, 8, 16, 20, 26, 40, 50, 75, 80, 100. Эти случаи деления не представляют трудности и для малоопытного счетчика. [№1, стр.36-38]
Попробовав на своем опыте нехитрые вычисления на счетах, я осознал всю легкость такого счета. Конечно, мне не хватало долговременной практики, но я уверен, что у опытного мастера счеты в руках – отличная замена карманному калькулятору. Понаблюдать за работой опытного «счетчика» я пошел в ближайший овощной магазин. Там работает продавец, которого я помнил с тех пор, как переехал на свою последнюю квартиру. Уже пожилой торговец, как часто бывает, не мог бросить старый метод и в начале 21-го века все считал на счетах. Да не просто считал, а считал чуть ли не быстрее «продвинутых» с электронными калькуляторами. Это ли не доказательство того, что счеты – изобретение на века?
§2 Умножение и деление без приборов.
Длительное время счет чисел выполняли только устно с помощью каких-либо предметов – пальцев, камешков, ракушек и др., а позже на специальных приборах – абаке, счетах. Только после того, как была изобретена позиционная система счисления и числа стали записывать цифрами индийские мудрецы нашли способ сложения чисел в письменном виде. При вычислениях они записывали числа папочкой на песке, насыпанном на специально приготовленную доску. Цифры, изображенные на песке, легко было стирать, а на их месте записывать другие. Вероятно, этим можно объяснить некоторые особенности индийского приема сложения чисел.
В Древней Индии было принято записывать слагаемые в столбик — одно под другим; сумму же записывали над слагаемыми, сложение начинали с наивысшего разряда, т. е. слева направо. Если записанная в сумме цифра при сложении последующего низшего разряда изменялась, то ранее записанную цифру стирали, а на ее место вписывали новую.
С XV века способ письменного сложения чисел принял современный вид. [№2, стр. 81-82]
Привожу краткую справку о том, когда впервые появились общеупотребительные теперь знаки арифметических действий и другие математические операторы:
+ и - в рукописях Леонардо-да-Винчи (1452-1519). В начале XV века действие сложения стали обозначать начальной буквой слова «плюс» (по латыни Р), что означало «сложить». До этого долгое время слагаемые просто записывали друг против друга без всякого знака. Древние египтяне обозначали сложение особым знаком – рисунком шагающих ног. Название «слагаемое» впервые встречается в работах математиков XIII в., а понятие «сумма» до XV века означало результат любого из четырех арифметических действий. Для обозначения вычитания в III в. до Н. э. В Греции использовали перевернутую букву пси (Ψ). Итальянские математики пользвались для обозначения вычитания буквой μ, начальной в слове «минус». Торговцы XVI в., отливая для продажи вино из бочек, черточкой мелом обозначали число мер проданного вина (вероятно, так произошел знак -). Чтобы отличить знак минус от тире, Л.Ф.Магницкий обозначал вычитание знаком ÷.
Х в сочинении Утреда (1631). Для обозначения действия умножения в XVI в. в Европе употребляли букву М, которая была начальной в латинском слове, обозначавшем увеличение – «мультипликация». В конце XVIII в. большинство математиков стали употреблять для обозначения умножения точку, но допускали и употребление косого креста.
. и : в сочинении Лейбница (1646-1716). На протяжении тысячелетий действие деления не обозначали каким-либо знаком – его просто называли и записывали словом. Индийские математики первыми стали обозначать деление первой буквой этого слова. До знака : у некоторых математиков встречался знак ÷ для обозначения деления.
![]() в сочинении Фибоначчи (1202). Арабы ввели для обозначения деления черту. От арабов этот знак перенял итальянский математик Фибоначчи.
в сочинении Фибоначчи (1202). Арабы ввели для обозначения деления черту. От арабов этот знак перенял итальянский математик Фибоначчи.
аnв сочинении Шюке (1484)
= в сочинении Р. Рекорда (Риккорда) (1557). Сам Риккорд объяснял этот знак так: «Никакие два предмета не могут в большей степени быть равны между собой, как две параллельные линии». Знак = стал общепризнанным благодаря авторитету знаменитого немецкого математика Готфрида Вильгельма Лейбница.
( ) и [ ] в сочинении Жирара. [№1, стр. 54; №2, стр. 80-87]
Предки наши пользовались гораздо более громоздкими и медленными приемами счисления. И если бы школьник XX века мог перенестись за четыре, за три века назад, он поразил бы наших предков быстротой и безошибочностью своих арифметических выкладок. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера счетного дела.
Принято думать, что арифметические знаки до известной степени интернациональны, что они одинаковы у всех народов европейской культуры. Это верно лишь по отношению к большинству знаков, но не ко всем. Знаки + и -, знаки х и : употребляются в одинаковом смысле и немцами, и французами, и англичанами. Но точка, как знак умножения, применяется не вполне тождественно разными народами Одни пишут 7 . 8, другие — 7 • 8, поднимая точку на середину высоты цифры. То же приходится сказать о знаке дробности, т. е. о знаке, отделяющем десятичную дробь от целого числа. Одни пишут как мы, 4,5, другие 4.5, третьи 4·5, помещая точку выше середины. Англичане и американцы совсем опускают ноль перед десятичной дробью, чего на континенте Европы никто не делает. В американской книге вы встречаете такие обозначения, как .725 или •725, или даже ,725 — вместо нашего 0,725.
Расчленение числа на классы обозначается также не однообразно. В одних странах разделяют классы точками (15.000.000), в других — запятыми (15,000,000). У нас привился разумный обычай не помещать между классами никакого знака, а оставлять лишь пробел (15000000).
Поучительно проследить за тем, как меняется способ наименования одного и того же числа с переходом от одного языка к другому. Число 18, например, мы называем «восемнадцать», т. е. произносим сначала единицы (8), потом десятки (10). В такой же последовательности читает это число немец: achtzehn, т. е. 8-10. Но француз произносит иначе: 10-8 (dix-huit). Насколько разнообразны у разных народов способы наименования того же числа 18, показывает следующее извлечение из таблицы, составленной одним исследователем:
по-русски ....….. 8-10
по-немецки ..... 8-10
по-французски…10-8
по-армянски ...…10+8
по-гречески ...…. 8+10
по-латыни ....….. без 2 20
по-новозеландски 11+7
по-валлийски …..3+5-10
по-литовски ...…..8 сверх 10
по-айносски …….10 — 2 сверх 10
по-коряцки …….. 3-5 сверх 10
Курьезно наименование для того же числа 18 у одного гренландского племени: «с другой ноги 3». При всей своей необычности это название, естественно, объясняется способом счета по пальцам рук и ног. Сходным образом объясняется карибское наименование числа 18: «все мои руки, 3, моя рука». [№1, стр. 26-28]
Особенно сложны и трудны были в старину действия умножения и деления — особенно последнее, «Умноженье — мое мученье, а с делением — беда», — говорили в старину. Тогда не существовало еще, как теперь, одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления — приемы один другого запутаннее, твердо запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.
В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» (1914) изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще (способы), скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках». Наш современный способ умножения описан там под названием «шахматного». Был также и очень интересный, точный, легкий, но громоздкий способ «галерой» или «лодкой», названный так в силу того, что приделении чисел этим способом получается фигура, похожая на лодку или галеру. У нас такой способ употреблялся до середины XVIII века. На протяжении своей книги в 640 страниц Леонтий Магницкий («Арифметика» - старинный русский учебник математики, которую Ломоносов называл «вратами своей учености») пользуется исключительно способом «галеры», не употребляя, впрочем, этого названия.
Упоминаются такие способы, как «загибанием», «решеткой», «задом наперед», «ромбом», «треугольником» и многие многие другие. Многие такие приемы для умножения чисел долгие и требуют обязательной проверки.
Любимым приемом проверки был так называемый «способ девятки». Этот изящный прием нередко описывается и в современных арифметических учебниках, особенно иностранных.
Проверка девяткой основана на «правиле остатков», гласящем: остаток от деления суммы на какое-либо число равен сумме остатков от деления каждого слагаемого на то же число. Точно так же остаток произведения равен произведению остатков множителей. С другой стороны, известно также, что при делении числа на 9 получается тот же остаток, что и при делении на 9 суммы цифр этого числа; например, 758 при делении на 9 дает остаток 2, и то же получается в остатке от деления (7 + 5 + 8) на 9. Сопоставив оба указанных свойства, мы и приходим к приему проверки девяткой, т. е. делением на 9.
Интересно, что и наш способ умножения не является совершенным; можно придумать еще более быстрые и еще более надежные. Одно из таких усовершенствований увеличивает надежность выполнения умножения. Оно состоит в том, что при многозначном множителе начинают с умножения не на последнюю, а на первую цифру множителя. Выглядит это так:
8713
Х 264
![]() 17426
17426
52278
![]() 34852
34852
2300232
Последнюю цифру каждого частного произведения подписывают под той же цифрой множителя, на которую умножают.
Преимущество подобного расположения в том, что цифры частных произведений, от которых зависят первые, наиболее ответственные цифры результата, получаются в начале действия, когда внимание еще не утомлено и, следовательно, вероятность сделать ошибку – меньшая.
Самым, на мой взгляд, «родным» и легким способом умножения является способ, который был употребителен у русских крестьян. Этот прием вообще не требует знания таблицы умножения дальше числа 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. В случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. [№1, стр. 50] Например:
23 х 17 ·
11 х 34 ·
5 х 68 ·
2 х 136
1 х 272; результат 272 + 68 + 34 + 17 = 391.
§3 Устный счет.
Жизнь для внимательного человека не только удивительно разнообразна, но и гениально проста. В полной мере эта фраза относится и к устному счету. Часто при арифметических действиях над числами можно облегчить свой труд, если знать основы арифметики и обладать некоторой смекалкой. Д.Р.Гончар рассказывает о следующих особенностях чисел, помогающих упростить счет:
Промежуточное приведение к «круглым» числам. Если хотя бы одно слагаемое близко к «круглому» числу десятков, сотен и др., т. е. А*10n – z, где z – сравнительно малое число, то вычисления можно упростить, приведя одно из слагаемых к ближайшему «круглому» числу и выполнив более легкое вычисление (затем, разумеется, учтя поправку).
Приведу пример, так как понять «с ходу» такой способ нелегко. (Дальше на каждый способ также будут приводиться примеры)
54 + 95 = 50 + 4 + 100 – 5 = 150 + 4 – 5 = 150 – 1 = 149.
Как видно из примера, полезно приводить слагаемые и к числам, кратным 50, 25 и т. д. Все зависит от конкретного случая и, повторюсь, от вашей смекалки. Такой способ кажется мне самым распространенным, причем многие проделывают такие вычисления автоматически, совсем не задумываясь над математическим смыслом и логичностью способа и уж тем более не догадываясь как он называется. Такому приему даже не надо учить, люди сами осваивают его в процессе изучения математики, постоянно сталкиваясь с такого рода вычислениями и ища пути полегче.
Использование изменения порядка счета. Интересный способ, позволяющий работать с большими числами. Заключается он в том, что при сложении чисел нередко бывает полезно складывать их, начиная со старших разрядов. Это существенно облегчает устное вычисление.
3264 + 2861 + 4100 = ? Складываем старший разряд слагаемых: 3 + 2 + 4 = 9; домножаем сумму на 10 (приписываем 0): 9*10 = 90; продолжаем прибавлять цифры следующего разряда:
90 + 2 + 8 + 1 = 101; повторяем операцию: 101*10 +6 +6 + 0 = 1010 + 12 = 1022; и еще раз:
1022*10 + 4 + 1 +0 = 10220 + 5 = 10225.
Эти же способы, слегка из изменив, можно применять и к вычитанию. Д.Р.Гончар предлагает и другие методы, но мне они кажутся чересчур надуманными, так как применимы они либо в очень ограниченном количестве случаев (например способ, в котором сумма нескольких слагаемых ищется по формуле суммы членом арифметической прогрессии), либо слишком сложны (как, например, складывание шестизначных чисел по разрядам попарно). [№6, стр.58, 61, Гончар Д.Р.]
Предложу еще один способ, которым всегда пользуюсь, когда ясно, что при вычитании получится отрицательное число. Принцип элементарен. Вытекает он из справедливости равенства
a – b = - (b – a).
Пример: 3627 – 9849 = ? Гораздо легче посчитать разность 9849 – 3627 = 6222. Результат (с минусом) и будет ответом: 3627 – 9849 = - 6222.
Можно облегчить и умножение, если, например, числа множителя делятся друг на друга:
32*36 = (32*3)*10 + (32*3)*2 = 96*10 +96*2 = 960 + 192 = 1152.
Облегчить умножение можно, использовав принцип «русского» способа умножения, о котором уже писалось в параграфе «Умножение и деление без приборов». Так, постепенно увеличивая один из множителей в n раз, а другой уменьшая в n раз, можно привести один из множителей к «круглому» виду:
75 * 24 = 75 * ![]() * 24 *
* 24 * ![]() = 100 * 18 = 1800.
= 100 * 18 = 1800.
Есть и еще способы, основанные на самых основных законах арифметики (распределительный и сочетательный). О них писать не имеет смысла.
Список литературы:
1. "Занимательная арифметика", Я.И.Перельман, издательство и год издательства не выяснены;
2. "Путешествие в историю математики", А.А.Свечников, изд. "Педагогика-Пресс", 1995 г.;
3. Еженедельник "Древо познания", изд. "МС ИСТ ЛИМИТЕД",
1. № 43 в России за 2003 г.;
2. № 73 в России за 2004 г.;
4. "Старинные занимательные задачи", С.Н.Олехник, Ю.В.Нестеренко, М.К.Потапов, изд. "Вита-Пресс", 1994 г.;
5. "Окно в удивительный мир информатики", М.Г.Коляда, изд. "Сталкер", 1997 г.;
6. "Устный счет и память", Д.Р.Гончар, А.Р.Лурия, В.В.Аткинсон, изд. "Сталкер", 1998 г.;
Похожие работы
... 100 10 1001=(9)10 100 11,1=(3,5)10 00 110 00 100 001 100 000 100 10 0 10 00 Таким образом, выполнение арифметических операций в двоичной системе счисления достаточно просто. Особенно просто выполнять операции сложения, вычитания и умножения. Благодоря этому, применение двоичной системы в вычислительных ...
... ; оптимальным решением при этом является "троичная система гирь": 1, 3, 9, 27,:, которая при взвешивании "порождает" троичную симметричную систему счисления, которая и была положена Н. П. Брусенцовым в основу троичного компьютера "Сетунь". Но автор двоичной арифметики в истории науки доподлинно известен: это известный немецкий математик Лейбниц (1646-1716), который в 1697 г. разработал правила ...
... рождения (год, число, месяц). 4. Подведение итогов. Домашнее задание. Учить записи в тетрадях. Заключение В данной курсовой работе было рассмотрена роль и место элективных курсов в предпрофильном обучении, а также разработан элективный курс не тему «система счисления» в предпрофильном обучении информатике. В первой части работы были выявлены главные особенности предпрофильной п
... последовательности 0 и 1. Например целое неотрицательное число А2=Т 111100002 будет храниться в ячейке следующим образом: 1 1 1 1 0 0 0 0 Значит, мы можем записать все числа от 0 до 255 в двоичной системе счисления в 1 ячейке памяти. 2.2 Представление чисел в компьютере Целые числа в компьютере хранятся в ячейках памяти, в этом случае каждому разряду ячейки памяти соответствует ...









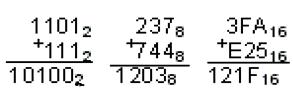
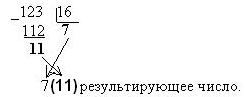
0 комментариев