1. МОДЕЛІ ПОВЕДІНКИ СПОЖИВАЧІВ
В теорії споживання вважається, що споживач керується принципом рацiональностi: вiн завжди прагне максимізувати свою корисність, i єдине, що його стримує, — це обмежений дохід:
max u(x) (1.1)
px = M
де х=(х1,...,хn)′ – вектор-стовпчик обсягів споживчих товарів, що придбав споживач за заданих цін; n – число різноманітних товарів; u(х) – функція корисності споживача; р = (p1,…,pn) – вектор-рядок цін товарів; М – обсяг доходу споживача.
Це задача на умовний екстремум, i її розв’язок зводиться до знаходження безумовного екстремуму функції Лагранжа:
L(x,λ)=u(x)-λ(px-M).
Необхідними умовами локального екстремуму є:
![]() (1.2)
(1.2)
![]()
![]() (1.3)
(1.3)
Точка екстремуму справді визначає точку максимуму, оскільки матриця Гессе U(х)= є вiд’ємно визначеною. З виразу (1.3) бачимо, що споживач за фіксованого доходу так обирає набір
є вiд’ємно визначеною. З виразу (1.3) бачимо, що споживач за фіксованого доходу так обирає набір ![]() , що в цій точці відношення граничної корисності дорівнює відношенню цін:
, що в цій точці відношення граничної корисності дорівнює відношенню цін:
![]()
Якщо розв’язати (1.2), (1.3) відносно ![]() , отримаємо функцію попиту споживача:
, отримаємо функцію попиту споживача:
![]()
2. РІВНЯННЯ СЛУЦЬКОГО
Розглянемо, як зміниться попит споживача, що визначається моделлю (1.1), якщо зміниться ціна одного з товарів. Нехай ціна n-го товару зросла на ![]() . Це приводить до такої зміни попиту на товари
. Це приводить до такої зміни попиту на товари
![]() (2.1)
(2.1)
де р – вектор-рядок цін; U – матриця Гессе; ![]() – вектор-стовпчик попиту на товари;
– вектор-стовпчик попиту на товари; ![]() – множник Лагранжа;
– множник Лагранжа; ![]() – індекс n за дужками біля матриці означає, що взято й n-й стовпчик.
– індекс n за дужками біля матриці означає, що взято й n-й стовпчик.
Проаналізуємо зміст складових, що входять у рівняння (2.1).
Зміна попиту за збільшення ціни з компенсацією доходу. Нехай дохід споживача збільшився на таку величину ![]() , яка компенсує споживачеві збільшення ціни на n-й товар (благо) на
, яка компенсує споживачеві збільшення ціни на n-й товар (благо) на ![]() .
.
Збільшення ціни з компенсацією доходу приводить до такої зміни попиту:
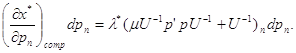 (2.2)
(2.2)
Тобто друга складова у правій частині рівняння (2.1) — це зміна попиту, якщо зростання ціни n-го товару на ![]() компенсується збільшенням доходу на
компенсується збільшенням доходу на ![]() .
.
Зміна попиту за зміни доходу. Якщо дохід змінюється на ![]() , то відповідно змінюється попит:
, то відповідно змінюється попит:
![]()
![]() (2.3)
(2.3)
Об’єднуючи вирази (2.1), (2.2), (2.3), отримаємо рівняння Слуцького, яке є серцевиною теорії корисності:
 (2.4)
(2.4)
Оскільки вивчається зміна попиту за зростання ціни на n-й товар, що не компенсується підвищенням доходу, то друга складова в (2.4) (з від’ємним знаком) знімає штучний приріст по спричинений компенсуючим зростанням доходу.
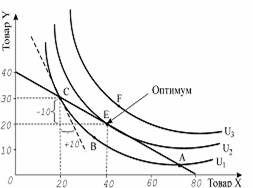
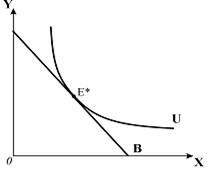
Ефект доходу полягає у змiнi споживання внаслідок зміни реального доходу, яка виникла через зміну цін.
Ефект заміщення полягає у змiнi споживання внаслідок зміни відносних цін.
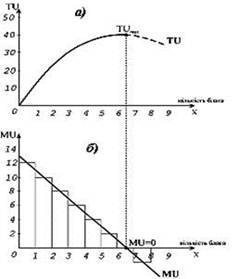
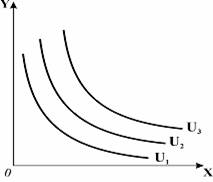
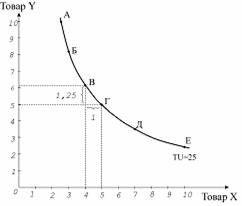
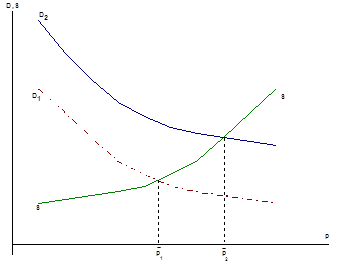
Графік представлено на малюнку 2.1
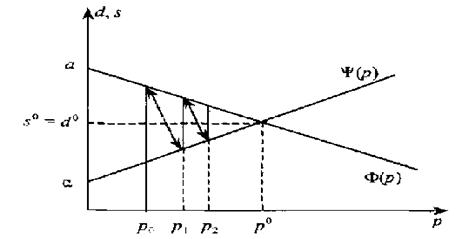
Малюнок 2.1 - Графік
3. МОДЕЛІ ПОВЕДІНКИ ВИРОБНИКІВ
Моделі оптимального (раціонального) вибору виробника (фірми). Нехай виробнича фірма випускає один продукт (чи багато продуктів, але з постійною структурою). Позначимо річний випуск у натурально-речовiй формі через Х – кількість одиниць продукту одного виду, вектор-стовпчик можливих обсягів різних видів ресурсів через х = (х1, ..., хn)′. Тоді технологія фірми визначатиметься її виробничою функцією, яка виражає зв'язок між випуском i витратами ресурсів:
Х=F(х).
Припускається, що F(х) двiчi неперервно диференційована, неокласична, i матриця її других похідних є вiд’ємно визначеною.
Якщо ![]() – вектор-рядок цін ресурсів, а р – ціна продукції, то кожному вектору витрат х вiдповiдає прибуток:
– вектор-рядок цін ресурсів, а р – ціна продукції, то кожному вектору витрат х вiдповiдає прибуток:
![]() (3.1)
(3.1)
У (3.1) ![]() – вартість річного випуску ô³рми, або її річний дохід,
– вартість річного випуску ô³рми, або її річний дохід, ![]() – витрати виробництва чи вартість витрат ресурсів за рік.
– витрати виробництва чи вартість витрат ресурсів за рік.
Якщо не вводити інших обмежень, крім невід’ємних обсягів витрат ресурсів, то задача знаходження максимуму прибутку набере вигляду:
![]()
![]() (3.2)
(3.2)
Це задача нелiнiйного програмування з n умовами невід’ємності: ![]() Необхідними умовами існування екстремуму є умови Куна-Таккера:
Необхідними умовами існування екстремуму є умови Куна-Таккера:
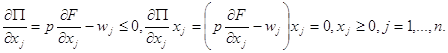 (3.3)
(3.3)
Якщо в оптимальному розв’язку використовуються всi види ресурсів, тобто ![]() , то умови (3.3) матимуть вигляд:
, то умови (3.3) матимуть вигляд:
![]() (3.4)
(3.4)
тобто в оптимальній точці вартість граничного продукту даного ресурсу повинна дорівнювати його цiнi.
Розглянемо задачу знаходження максимуму випуску за заданого обсягу витрат
![]() (3.5)
(3.5)
Це задача нелiнiйного програмування з одним лiнiйним обмеженням i умовою невiд’ємностi змінних. Побудуємо функцію Лагранжа
![]()
і знайдемо її максимум за умови невiд’ємностi змiнних. Для цього необхідно, щоб виконувались умови Куна-Таккера:
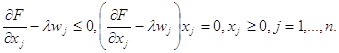 (3.6)
(3.6)
Як бачимо, якщо покласти ![]() , умови (3.6) збiгаються з умовами (3.3).
, умови (3.6) збiгаються з умовами (3.3).
Похожие работы
... Як найповніше задовольнити ці потреби? Досліджувати споживачів, їхні уподобання, смаки та реакції на маркетингові заходи. 1.3 Дослідження поведінки організацій-споживачів Часом покупцем є не індивідуальний споживач, а організація-споживач. Якщо підприємство пропонує свій товар на ринку організацій-споживачів, воно здійснює промисловий маркетинг. Ринок організацій-споживачів – це сукупність ...
... що для вивчення вжитку як складовій частині культурного процесу потрібні фахівці з абсолютно іншим типом освіти і наукового досвіду. Розділ 2 Еволюційний розвиток ринкової поведінки 2.1. Основні теорії моделей ринкової поведінки. Поведінка споживачів В основі формування ринкового попиту лежать рішення споживачів. Модель поведінки споживача будується за загальними правилами мікроекономі ...
... про час купівлі часто визначається цілим рядом факторів, Приміром. ви можете купити товар швидше, якщо одна з марок, якій ви віддаєте перевагу наявна у продажу або якщо її виробник пропонує знижку. Поведінка споживача після купівлі Останній етап процесу прийняття рішення про купівлю - це поведінка споживача після купівлі, тобто порівняння споживачем придбаного товару зі своїм и надіями чи споді ...
... сировинної орієнтації країн у зовнішньоекономічній діяльності. Яскравим прикладом запровадження цієї моделі є Росія, Україна. Розділ 2. Моделювання рівноваги попиту та пропозиції 2.1 Аналіз підходів щодо моделювання моделей сукупного попиту та пропозиції У процесі розширення сфери застосування математичного моделювання в економіці традиційно створювалися програмні системи багатовимірного ...


0 комментариев