Выбор метода исследования, его обоснование, описание

2.2 Выбор метода исследования, его обоснование, описание

В данной курсовой работе выбираем метод наименьших квадратов с весами. В методе каждому отклонению Е придается вес, для того чтобы более точнее определить влияние прогнозного значения показателя. Чаще всего метод применяется, если исследуемая продукция является сезонной, так как значение показателя меняется в определенные промежутки времени. Исследуемой продукцией данной курсовой работы являются кирпичи, которые в свою очередь являются сезонной продукцией.

Экстраполяция выполненной с помощью МНК тенденции изменений показателя на прогнозный период предполагает, что все наблюдения (уровни временного ряда) равнозначны для прогноза. Однако информация об изменении показателя в период времени, непосредственно примыкающий к моменту прогноза, «ценнее» для прогнозирования, чем в более удаленный. Но и более удаленные от момента прогноза наблюдения временного ряда также несут значительную информацию о процессе, поэтому пренебрегать этими наблюдениями при расчете прогноза не следует.

Для учета различной «ценности», или, как это принято в терминологии прогнозирования и информатики, «веса» информации в различные моменты времени применяют метод наименьших квадратов с весами (МНКВ) и метод экспоненциального сглаживания.

Рассмотрим метод наименьших квадратов с весами.

Суть метода заключается в том, что каждому отклонению E придается вес β_t < 1, причем веса возрастают для точек, находящихся ближе к моменту прогнозирования. Следовательно, чем дальше наблюдение (уровень) стоит от момента прогноза, тем меньший вес оно имеет, тем меньшее влияние оказывает на формирование уровня прогнозного значения показателя.

Для определения веса β_t удобно использовать выражение:

β_t=α^n-(t-1) (2.1)

где – α некоторое число, меньшее единицы; n – число наблюдений. Чем меньше величина α, тем меньше ранние наблюдения влияют на прогноз.

Условие для МНКВ запишется в виде:

∑β[x_t-f(t)]²→min (2.2)

Система нормальных уравнений для МНКВ имеет вид:

∑β_x=a∑β+b∑β_t+с∑ β_t

∑_βxt= a∑β_t+b∑β_t²+ с∑ β_t² (2.3)

∑_βxt= a∑β_t²+b∑β_t³+ с∑ β_t⁴

2.3 Расчет искомых показателей

За последние три месяца на предприятии «Атлант» по производству кирпичей наметился спад объёма продаж, и как следствие объёма прибыли.

Директором предприятия был принят ряд мер, направлённых на увеличение объёма продаж (реклама, различные методы стимулирования сбыта и т.п.).

Проведите исследование системы управления предприятием и определите:

а)способствовала ли проведённая кампания увеличению объёма продаж;

б)как при сохраняющейся тенденции изменится объём продаж предприятия через 5 лет;

в)отразите возможный диапазон изменения прибыли предприятия на период 2009-2013 гг.

г)оцените эффективность предлагаемых мероприятий через 3 года при темпе инфляции 12%

д)существует ли зависимость объёма продаж предприятия от затрат на рекламу продукции кирпичей.

Исходные данные приведены в таблице 2.

Таблица 2.1 - Объем продаж предприятия «Атлант» за 14 лет

Порядковый год работы предприятия “Атлант”	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Объём продаж предприятия за год (тыс. руб.)	3500	4800	5000	2900	3650	3490	3330	3170	3010	2850	2690	2530	2370	2210

Анализ условия задачи позволяет выделить факторный и результативный показатели:

1)факторный показатель х – порядковый год работы предприятия “Атлант”, 1,2,3 …..12,13,14;

2)результативный показатель у – объём продаж предприятия за год(тыс. руб.) .

Строим график зависимости объема продаж от времени работы предприятия на основании таблице 2.1

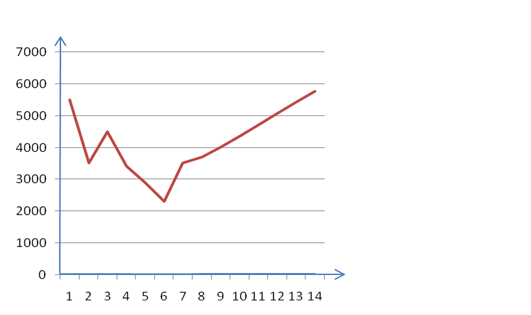
Рисунок 1 - График зависимости объема продаж от времени работы предприятия

В соответствии с требованиями метода наименьших квадратов для определения параметров а, b и c необходимо решить следующую систему уравнений:

∑β_x=a∑β+b∑β_t+с∑ β_t

∑_βxt= a∑β_t+b∑β_t²+ с∑ β_t² (2.3)

∑_βxt= a∑β_t²+b∑β_t³+ с∑ β_t⁴

Для того чтобы более ранняя информация оказывала влияние на прогноз альфа (α) принимается ≈1, (α=0,9)

Составляем таблицу 2.2 для расчета прогноза объема продаж предприятия на период 2009-2013гг., если известна динамика объема продаж за предыдущие 14 лет.

Таблица 2.2 - Динамика объема продаж на период 1995-2008 гг.

Год	Объём продаж предприятия за год (тыс. руб.) (Х)	t	t2	t3	t4	xt	xt2
1995	3500	1	1	1	1	3500	3500
1996	4800	2	4	8	16	9600	19200
1997	5000	3	9	27	81	15000	45000
1998	2900	4	16	64	256	11600	46400
1999	3650	5	25	125	625	18250	91250
2000	3490	6	36	216	1296	20940	125640
2001	3330	7	49	343	2401	23310	163170
2002	3170	8	64	512	4096	25360	202880
2003	3010	9	81	729	6561	27090	243810
2004	2850	10	100	1000	10000	28500	285000
2005	2690	11	121	1331	14641	29590	325490
2006	2530	12	144	1728	20736	30360	364320
2007	2370	13	169	2197	28561	30810	400530
2008	2210	14	196	2744	38416	30940	433160
сумма	45500	105	1015	11025	127687	304850	2749350

На основании формулы 2.1 и таблицы 2.2 рассчитываем коэффициент β:

β ₁=α¹⁴=0,26

β ₂=α¹³=0,28

β ₃=α¹²=0,31

β ₄=α¹¹=0,34

β ₅=α¹⁰=0,37

β ₆=α⁹=0,41

β ₇=α⁸=0,45

β ₈=α⁷=0,49

 β ₉=α⁶=0,54

β ₁₀=α⁵=0,60

β ₁₁=α⁴=0,66

β ₁₂=α³=0,73

β ₁₃=α²=0,81

β ₁₄=α¹=0,9

∑β=7,15

β_x=0,9¹⁴*3500+0,9¹³*4800+0,9¹²*5000+0,9¹¹*2900+0,9¹⁰*3650+0,9⁹*3490+0,9⁸*3330+0,9⁷*3170+0,9⁶*3010+0,9⁵*2850+0,9⁴*2690+0,9³*2530+0,9²*2370+0,9¹**2210=801,50+1214,40+1410+907,70+1270,20+1350,63+1431,90+1521,60+1598,31+1681,50+1764,64+1844,37+1919,70+1989=20705,45

∑β_t=0,9¹⁴*1+0,9¹³*2+0,9¹²*3+0,9¹¹*4+0,9¹⁰*5+0,9⁹*6+0,9⁸*7+0,9⁷*8+0,9⁶*9+0,9⁵*10+0,9⁴*11+0,9³*12+0,9²*13+0,9¹*14=0,26+0,506+0,846+1,252+1,74+2,322+3,01+3,824+4,779+5,9+7,216+8,748+10,53+12,6=65,3

∑β_t²=0,9¹⁴*1+0,9¹³*4+0,9¹²*9+0,9¹¹*16+0,9¹⁰*25+0,9⁹*36+0,9⁸*49+0,9⁷*64+0,9⁶*81+0,9⁵*100+0,9⁴*121+0,9³*144+0,9²*169+0,9¹*196=0,229+1,012+2,538++5,008+8,7+13,932+21,07+30,592+43,011+59+79,376+104,976+136,89+176,4==684,65

∑β_t³=0,9¹⁴*1+0,9¹³*8+0,9¹²*27+0,9¹¹*64+0,9¹⁰*125+0,9⁹*216+0,9⁸*343+0,9⁷*512+0,9⁶*729+0,9⁵*1000+0,9⁴*1331+0,9³*1728+0,9²*2197+0,9¹*2744=0,229+2,024+7,614+20,032+43,5+83,59+147,5+244,73+387,1+590+873,14+1259,7+1779,57+2469,6=7908,099

∑β_t⁴=0,9¹⁴*1+0,9¹³*16+0,9¹²*81+0,9¹¹*256+0,9¹⁰*625+0,9⁹*1296+0,9⁸*2401+0,9⁷*4096+0,9⁶*6561+0,9⁵*10000+0,9⁴*14641+0,9³*20736+0,9²*28561+0,9¹*38416=0,229+4,048+22,842+8,0128+217,5+501,55+1032,43+1957,89+3483,89++5900+9604,5+15116,54+23134,41+34574,4=95558,2

∑β_xt=0,9¹⁴*3500+0,9¹³*9600+0,9¹²*15000+0,9¹¹*11600+0,9¹⁰*18250+0,9⁹*20940+0,9⁸*23310+0,9⁷*25360+0,9⁶*27090+0,9⁵*28500+0,9⁴*29590+0,9³*30360+0,9²*30810+0,9¹*30940=910+2688+4650+3944+6752,50+8585,40+10489,50+12426,40+14628,60+17100+19529,40+22162,80+24956,10+27846=176668,70

∑β_xt²=0,9¹⁴*3500+0,9¹³*19200+0,9¹²*45000+0,9¹¹*46400+0,9¹⁰*91250+0,9⁹*125640+0,9⁸*163170+0,9⁷*202880+0,9⁶*243810+0,9⁵*285000+0,9⁴*325490+0,9³*364320+0,9²*400530+0,9¹*433160=910+5376+13950+15776+33762,50+51512,40+73426,50+99411,20+131657,40+171000+214823,40+265953,60+324429,30+389844=1791832,30

Теперь составляем систему:

20705,45=7,15a+65,3b+684,65с;

176668,70=65,3a+684,65b+7908,099с;

1791832,30 =684,65а+7908,099b+95558,2c.

Параметры а, b и с находим способом определений. Сначала найдём общий определитель

∆ = 7,15 65,3 684,65

65,3 684,65 7908,099

684,65 7908,099 95558,2 = 7,15*684,65*95558,2+684,65*95558,2*7,15+ 684,65*7,15*95558,2-(684,65)³-(7908,099)²*7,15-5,3)²*95558,2=945708,5

После этого определяем частные определители Δа, Δb, Δс:

∆а = 20705,45 65,3 684,65

176668,70 684,65 7908,099 = 14512414123

1791832,30 7908,099 95558,2

∆b= 7,15 20705,45 684,65

65,3 176668,70 7908,099 =-2178654210

684,65 1791832,30 95558,2

∆ =с 7,15 65,3 20705,45

 65,3 684,65 176668,70 = 147876534

 684,65 7908,099 1791832,30

Отсюда определяем коэффициенты а, b и с:

а = ∆а/а = 14512414123/ 945708,5 = 15345,55;

b = ∆b = -2178654210/ 945708,5 = - 2303,73;

c = ∆c = 147876534/945708,5 = 156,37.

Уравнение параболы имеет вид:

 

X=15345,55-2303,73t+156,37t²

Теперь составляем таблицу 2.3 прогноза t=15,16,17,18,19, подставляя в полученное уравнение параболы, затем строим график:

Таблица 2.3 - Динамика объема продаж кирпичей на период 2009-2013 гг.

Год	Объём продаж предприятия за год (тыс. руб.)
2009	15972,85
2010	18516,59
2011	21373,07
2012	24542,29
2013	28024,25

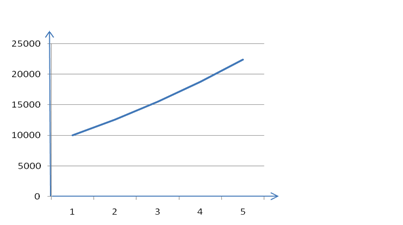
Рисунок 2 – График динамики объема продаж кирпичей на период 2009-2013гг.

Прогноз объема продаж предприятия в таблице 2.1 составлен на период 1995-2008гг. При сохраняющейся тенденции объем продаж предприятия через 5 лет будет увеличиваться.

Основным показателем эффективности предприятия является чистодисконтированный доход (ЧЧД), чтобы его найти нужно, составить прогноз выручки на последующие 3 года.

Таблица 2.4 - Динамика изменения выручки на период 1995-2008 гг.

Год	Объем продаж, тыс. руб.	Себестоимость продукции, тыс. руб.	Выручка, тыс. руб.
1	2	3	4
1995	3500	2450	1050
1996	4800	3360	1440
1997	5000	3500	1500
1998	2900	2030	870
1999	3650	2555	1095
2000	3490	2443	1047
2001	3330	2331	999
2002	3170	2219	951
2003	3010	2107	903
2004	2850	1995	855
2005	2690	1883	807
2006	2530	1771	759
2007	2370	1659	711
2008	2210	1547	663
сумма	45500	31850	13650

Следующим действием является построение графика зависимости выручки от времени работы предприятия на основании таблицы 2.4.

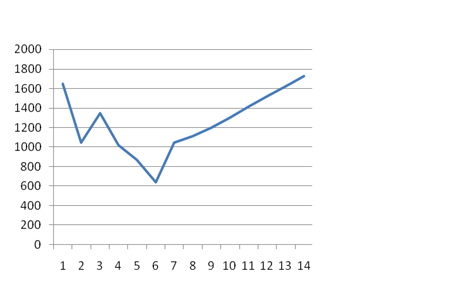
Рисунок 3 - График зависимости выручки предприятия от времени его работы

Анализ графика, изображенного на рисунке 3, показывает, что при небольшом увеличении факторного показателя Х на определенную величину наблюдается неравномерное возрастание значений результативного показателя У.

Таким образом, связь между показателями описывается при помощи уравнения параболы:

 

Ух=a+bx+cx² ,

где Ух – результативный показатель; Х – факторный показатель; а, b, c –параметры уравнения регрессии.

Таблица 2.5 - Прогноз выручки на период 1995-2008 гг.

Год	Выручка, тыс. руб.	t	t2	t3	t4	xt	xt2
1995	1050	1	1	1	1	1050	1050
1996	1440	2	4	8	16	2880	5760
1997	1500	3	9	27	81	4500	13500
1998	870	4	16	64	256	3480	13920
1999	1095	5	25	125	625	5475	27375
2000	1047	6	36	216	1296	6282	37692
2001	999	7	49	343	2401	6993	48951
2002	951	8	64	512	4096	7608	60864
2003	903	9	81	729	6561	8127	73143
2004	855	10	100	1000	10000	8550	85500
2005	807	11	121	1331	14641	8877	97647
2006	759	12	144	1728	20736	9108	109296
2007	711	13	169	2197	28561	9243	120159
2008	663	14	196	2744	38416	9282	129948
сумма	13650	105	1015	11025	127687	91455	824805

∑β_x=a∑β+b∑β_t+с∑ β_t

∑_βxt= a∑β_t+b∑β_t²+ с∑ β_t² (2.3)

∑_{β xt}= a∑β_t²+b∑β_t³+ с∑ β_t⁴

∑β_x=0,9¹⁴*1050+0,9¹³*1440+0,9¹²*1500+0,9¹¹*870+0,9¹⁰*1095+0,9⁹*1047+0,9⁸*999+0,9⁷*951+0,9⁶*903+0,9⁵*855+0,9⁴*807+0,9³*759+0,9²*711+0,9¹*633=273+403,20+465+295,80+405,15+429,27+449,55+465,99+487,62+513+532,62+554,07+575,91+569,70=6419,88

∑β_t=0,9¹⁴*1+0,9¹³*2+0,9¹²*3+0,9¹¹*4+0,9¹⁰*5+0,9⁹*6+0,9⁸*7+0,9⁷*8+0,9⁶*9+0,9⁵*10+0,9⁴*11+0,9³*12+0,9²*13+0,9¹*14=0,26+0,506+0,846+1,252+1,74+2,322+3,01+3,824+4,779+5,9+7,216+8,748+10,53+12,6=65,3

∑β_t²=0,9¹⁴*1+0,9¹³*4+0,9¹²*9+0,9¹¹*16+0,9¹⁰*25+0,9⁹*36+0,9⁸*49+0,9⁷*64+0,9⁶*81+0,9⁵*100+0,9⁴*121+0,9³*144+0,9²*169+0,9¹*196=0,26+1,012+2,538++5,008+8,7+13,932+21,07+30,592+43,011+59+79,376+104,976+136,89+176,4=684,65

∑β_t³=0,9¹⁴*1+0,9¹³*8+0,9¹²*27+0,9¹¹*64+0,9¹⁰*125+0,9⁹*216+0,9⁸*343+0,9⁷*512+0,9⁶*729+0,9⁵*1000+0,9⁴*1331+0,9³*1728+0,9²*2197+0,9¹*2744=0,26+2,024+7,614+20,032+43,5+83,59+147,5+244,73+387,1+590+873,14+1259,7+1779,57+2469,6=7908,099

∑β_t⁴=0,9¹⁴*1+0,9¹³*16+0,9¹²*81+0,9¹¹*256+0,9¹⁰*625+0,9⁹*1296+0,9⁸*2401+0,9⁷*4096+0,9⁶*6561+0,9⁵*10000+0,9⁴*14641+0,9³*20736+0,9²*28561+0,9¹*38416=0,26+4,048+22,842+8,0128+217,5+501,55+1032,43+1957,89+3483,89++5900+9604,5+15116,54+23134,41+34574,4=95558,2

∑β_xt=0,9¹⁴*1050+0,9¹³*2880+0,9¹²*4500+0,9¹¹*3480+0,9¹⁰*5475+0,9⁹*6282+0,9⁸*6993+0,9⁷*7608+0,9⁶*8127+0,9⁵*8550+0,9⁴*8877+0,9³*9108+0,9²*9243+0,9¹*9282=273+806,40+1395+1183,20+2025,75+2575,62+3146,85+3727,92+4388,58+5130+5858,82+6648,84+7486,83+8353,80=53000,61

∑β_xt²=0,9¹⁴*1050+0,9¹³*5760+0,9¹²*13500+0,9¹¹*13920+0,9¹⁰*27375+0,9⁹*37692+0,9⁸*48951+0,9⁷*60864+0,9⁶*73143+0,9⁵*85500+0,9⁴*97647+0,9³*109296+0,9²*120159+0,9¹*129948=273+1612,80+4185+4732,80+10128,75+15453,72+22027,95+29823,36+39497,22+51300+64447,02+79786,08+97328,79+116953,20=537549,69.

Теперь составляем систему:

6419,88=7,15a+65,3b+684,65с

 53000,61=65,3a+684,65b+7908,099с

537549,69=684,65а+7908,099b+95558,2c

Параметры а, b и с находим способом определений. Сначала найдём общий определитель:

∆ = 7,15 65,3 684,65

 65,3 684,65 7908,099

 684,65 7908,099 95558,2

= 7,15*684,65*95558,2+684,65*95558,2*

*7,15+684,65*7,15*95558,2-(684,65)³-(7908,099)²*7,15-5,3)²*95558,2=945708,5

После этого определяем частные определители Δа, Δb, Δс:

∆а = 6419,88 65,3 684,65

53000,61 684,65 7908,099 = 14787644136

537549,69 7908,099 95558,2

∆b = 7,15 6419,88 684,65

65,3 53000,61 7908,099 = -3654558712

684,65 537549,69 95558,2

Δc = 7,15 65,3 6419,88

65,3 684,65 53000,61 = 241475863,5

684,65 7908,099 537549,69

Отсюда определяем коэффициенты а, b и с:

a = ∆a =14787644136/945708,5= 15636,58;

b = ∆b = -3654558712/945708,5= 3864,36 ;

c = ∆c =241475863,5 / 945708,5= 255,34.

Уравнение параболы имеет следующий вид:

 

X=15636,58-3864,36 t+225,34t²

Составляем таблицу 2.6 прогноза выручки на период 2009-2011гг.

 

X=15636,58-3864,36 t+225,34t² ; где t=15, 16, 17.

Таблица 2.6 - Прогноз выручки на период 2009-2011гг.

Год	2009	2010	2011
Выручка, тыс. руб.	8372,68	11493,86	15665,72

Затем рассчитываем чистодисконтированный доход (ЧДД):

ЧД=∑f_m; (2.5)

ЧДД=ЧД* α_m; (2.6)

ЧДД=∑f_m*α_{m ;} (2.7)

α_m=1/(E+1)^{tm ;} (2.8)

где α_m – коэффициент дисконтирования; E-норма дисконта; F_m-денежный поток на m-ом шаге расчета; E= темпу инфляции=12%=0,12.

ЧД=8372,68+11493,86+15665,72=35532,26

ЧДД=8372,68*1/(1+0,12)+11493,86*1/(1+0,12)+15665,72*1/(1+0,12)=31725,24

Для того чтобы определить существует ли зависимость объема продаж на предприятии от затрат на рекламу кирпичей надо рассчитать коэффициент корреляции и корреляционное отношение.

Коэффициент корреляции рассчитывается по формуле:

(2.9)

Таблица 2.7 - Данные для расчета коэффициента корреляции

N	x	y	xy	x^2	y^2
1	35	3500	122500	1225	12250000
2	48	4800	230400	2304	23040000
3	50	5000	250000	2500	25000000
4	29	2900	84100	841	8410000
5	37	3650	135050	1369	13322500
6	35	3490	122150	1225	12180100
7	33	3330	109890	1089	11088900
8	32	3170	101440	1024	10048900
9	30	3010	90300	900	9060100
10	29	2850	82650	841	8122500
11	27	2690	72630	729	7236100
12	25	2530	63250	625	6400900
13	24	2370	56880	576	5616900
14	22	2210	48620	484	4884100
сумма	456	45500	1569860	15736	156661000

Теперь подставляя данные из таблицы 2.7 в формулу, рассчитываем коэффициент корреляции:

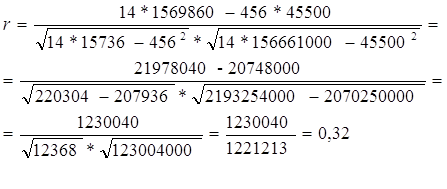
R= 0,32

По модулю коэффициент корреляции получился равным 1,01, что означает наличие зависимости между фактором влияния и областью, на которую влияют факторы.

Находим корреляционное отношение, которое рассчитывается по формуле:

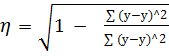 (2.10)

Анализ условия задачи позволяет выделить факторный и результативный показатели:

факторный показатель x – затраты на рекламу;

результативный показатель у – объем продаж предприятия тыс. руб

Строим график зависимости объема продаж от затрат на рекламу на основании таблицы 2.7.

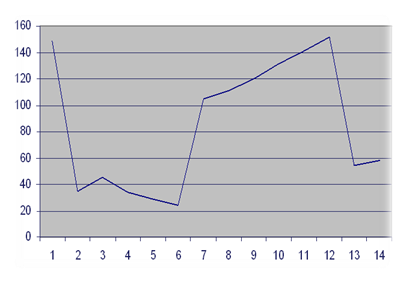
4 - График зависимости объема продаж от затрат на рекламу

Анализ графика, изображенного на рисунке 4, показывает, что при изменении факторного показателя Х значения результативного показателя У изменяется несоответственно факторному показателю X.

Для записи такой зависимости подходит показательное уравнение прямой:

Y=ax^b (2.11)

где Ух – результативный показатель; Х – факторный показатель; а, b –параметры уравнения регрессии.

В соответствии с требованиями метода наименьших квадратов с весами для определения параметров а и b необходимо решить следующую систему уравнений:

(2.12)

Σy=na+bΣx

Σyx=aΣx+bΣx²

Так как уравнение прямой показательное нужно сделать замену путем логарифмирования:

Y=ax^b(2.13)

(2.14)

ΣY=nA+bΣX

ΣYX=aΣX+bΣX²

где Lnx=X; lny=Y; lna=A → Y=A+bX

Составляем таблицу 2.8 для расчета корреляционного отношения:

Таблица 2.8 - Данные для расчета корреляционного отношения

n	x	y	lnX(X)	lny(Y)	lnX*lnY	(lnX)^2	y-расч.	(y-y)^2р	(y-y)^2с
1	35	3500	3,55	8,16	28,97	11,23	0,02	2745698742	2745700000
2	48	4800	3,87	8,47	32,78	14,98	0,02	3135687789	3135690000
3	50	5000	3,91	8,51	33,28	15,29	0,02	3035547891	3035550000
4	29	2900	3,36	7,97	26,78	11,29	0,02	2256652317	2256660000
5	37	3650	3,61	8,20	29,61	13,04	0,02	3264124178	3264130000
6	35	3490	3,55	8,15	28,94	12,61	0,02	2835874548	2835880000
7	33	3330	3,49	8,11	28,31	12,18	0,02	3145874693	3145880000
8	32	3170	3,46	8,06	27,89	11,98	0,02	2857469823	2857470000
9	30	3010	3,40	8,00	27,20	11,56	0,02	3275487746	3275490000
10	29	2850	3,36	7,95	26,72	11,29	0,02	3269874547	3269880000
11	27	2690	3,29	7,89	25,96	10,83	0,02	2368758969	2368760000
12	25	2530	3,21	7,83	25,14	10,31	0,02	2453997595	2454000000
13	24	2370	3,17	7,77	24,63	10,05	0,02	2446213587	2446220000
14	22	2210	3,09	7,70	23,80	9,55	0,02	2358795462	2358800000
Всего	456	45500	48,32	112,77	390,02	166,19	0,30	44525380179	44552400000

112,77=14A+48,32b

390,02=48,32A+166,19b

Первое уравнение умножаем на 3,9 и отнимаем от второго уравнения первое.

439,80=48,32A+144,96b

390,02=48,32A+166,19b

728,33=311,15b

b=1,34

Во второе подставляем значение b и находим A

390,02=48,32A+222,70

390,02=48,32А+222,70

-4,31=48,32А

А=-0,09

А=lna → a=10^A→ a=10^-0.09=0,9

Yр=0, 9*x^{1, 34} – расчетное значение y

Yс – среднее значение

По формуле рассчитываем корреляционное отношение:

n=1-( 44525380179/44552400000)=1,00;

n=0;

Зависимости между факторным (X) и результативным (Y) показателями, является нелинейной, так как η < r.

η=0; r=0,32 → 0<0,32

y=a*x^b

y=0,9*x^-0,09

Таблица 2.9 - Теоретические значения затрат на рекламу

x	35	48	50	29	37	35	33	32	30	29	27	25	24	22
y	0,017	0,018	0,019	0,016	0,017	0,17	0,016	0,016	0,017	0,017	0,017	0,017	0,017	0,017

Вывод: таким образом, на основании вышеприведённых расчётов можно утверждать, что аппарат управления работает эффективно и принимаемые управленческие решения способствуют росту объёма продаж и объему прибыли продукции.

Заключение

Выбор параметрического подхода к исследованию оказывает самоесущественное влияние на процесс его проведения и результативность, так как от этого во многом зависит направленность всех исследовательских работ. Большая часть изучаемых объектов - динамичные, внутренне взаимосвязанные объекты, взаимодействующие с внешней средой, поэтому одним из наиболее приемлемых подходов их исследования является параметрический. Данный подход происходит из сущности параметров, которые представляют собой учение о всеобщих связях явлений и наиболее общих закономерностях развития бытия и мышления. Базовым законом этого учения выступает закон единства и борьбы противоположностей, а основополагающим принципом - принцип всеобщих связей явлений. Это значит, что для изучения какого-либо предмета необходимо рассмотреть все его стороны и параметры. При этом развитие, как общий процесс, проходит периодически повторяющиеся ступени, но каждый раз на более высоком уровне и все это осуществляется по спирали.

Параметрический подход во многом определил развитие целого спектра других подходов, и в первую очередь системного.Он рассматривает управленческую деятельность как непрерывное выполнение комплекса определенных взаимосвязанных между собой видов деятельности и общих функций управления (прогнозирование и планирование, организация и т.д.). Причем выполнение каждой работы и общих функций управления здесь также рассматриваются в виде процесса, т.е. как совокупность взаимосвязанных непрерывно выполняемых действий, преобразующих некоторые входы ресурсов, информации и т.п. в соответствующие выходы, результаты.

Во второй части курсовой работы я проводил исследование системы управления на предприятии «Атлант» по производству кирпичей. В ходе исследования я выявил, что проведенная кампания способствовала увеличению объема продаж. В последующие годы сохранялась тенденция увеличения объема продаж. При темпе инфляции 12% выручка не уменьшалась, а наоборот увеличивалась. Рассчитанный коэффициент корреляции r=0,32 показывает, что фактор затрат на рекламу оказывает высокое влияние на объём прибыли, т.е. существует связь между объёмом прибыли и рекламой (принятые меры способствовали увеличению объема продаж). Положительное значение коэффициента корреляции свидетельствует о наличии прямой связи между затратами на рекламу и объёмом прибыли.

Список использованных источников

1.Глущенко В.В., Глушенко И.И. Исследование систем управления: 2007

2.Игнатьева А.В., Максимцов М.М. Исследование систем управления: Учебное пособие. - М.: ЮНИТИ-ДАНА, 2007.

3.Короткое Э.М. Исследование систем управления: Учебник. - М.: ДЕКА, 2008.

4.Мельник М.В. Анализ и оценка систем управления на предприятиях. - М.: Финансы и статистика, 2007.

5.Мишин В.М. Исследование систем управления: Учебное пособие. - М.: Финансы и статистика, 2007.

6.Рузавин Г.И. Методология научного исследования: Учебное пособие. - М.: ЮНИТИ-ДАНА, 2007.