Навигация
1.2 Матричні способи
До матричних способів відносяться: матриці (суміжності, інциденції, цикломатичні), n-мірні таблиці (масиви), n-мірні куби.
Матриця суміжності А – це квадратна матриця, що задає топологію системи і має наступний вигляд:
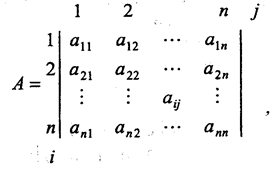
Матрицями суміжності можна задавати топології, що описуються як орієнтованими графами, так і неорієнтованими графами.
Для систем, топологія яких задається орієнтованим графом, розрізняють два типи матриці суміжності з’єднань за виходами.
Матриця суміжності з’єднань за входами – це така матриця суміжності, в якій рядки позначені елементами (номерами елементів) системи, входи яких з’єднані з виходами тих елементів системи, якими позначені стовпці матриці.
Тобто, якщо в цій матриці Аij=1, то це означає, що вхід і-го елеметна системи з’єднаний з виходом j-го елемента.
Так, наприклад, для топології, що на рис.1.1., матриця суміжності з’єднань за входами АІ буде такою:
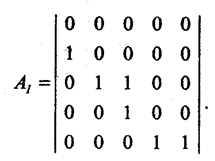
Матриця суміжності з’єднань за виходами – це така матриця суміжності, в якій рядки позначені елементами системи, якими розначені стовпчі матриці.
Тобто, якщо в такій матриці aij=1, то це означає, що вихід i-го елемента системи з’єднаний з входом j-го елемента.
Для тієї ж топології, що на рис.1.1, матриця суміжності з’єднань за виходами Ао буде такою:
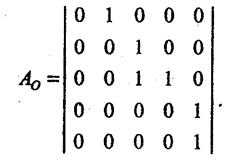
Для задання топології систем, що описується неорієнтованим графом, застосовують тільки одну матрицю суміжності А, яка є об’єднанням матриць АІ та Ао
А= АІ![]() АО.
АО.
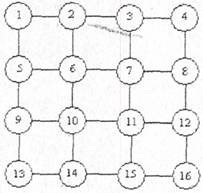
Так, наприклад, для топології, що на рис. 1.3, матриця суміжності А буде такою:
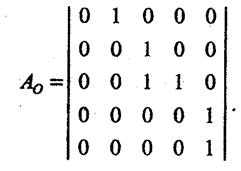
Для задання топологій систем іноді застосовують матриці інциденцій
Якщо топологія задається орієнтованим графом G=(B,E), де B={b1,b2,…bn}, D={d1,d2,…dm}, то матриця інциденцій для дуг S матиме такий вигляд:

Наприклад, для топології, що на рис. 1.2., матриця інциденції для дуг S буде такою:

Якщо топологія задається неорієнтованим графом G=(B,E), де B={b1,b2,…bn}, D={d1,d2,…dm}, то матриця інциденцій для ребер R матиме такий вигляд:
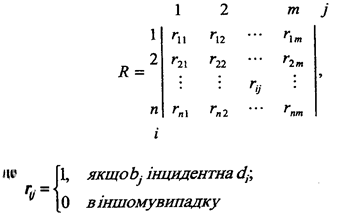
Для топології, що на рис 1.3. матриця інциденції для ребер R буде такою:

Цикломатичні матриці, яких ще називають другі матриці інциденції, можуть застосовуватися для опису топологій, що містять v незалежних циклів (контурів). Вони мають такий вигляд:

Так, наприклад, для топології, що на рис. 1.3., цикломатична матриця С, що має один незалежний контур, буде такою:
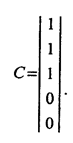
Можна легко зауважити, що для задання топології цикломатичні матриці є непридатними, бо у випадку відсутності в топології контурів, що часто буває в топологічних системах, такі матриці містять лише нулі, а тому топології не описують.
Матриці інциденції можуть застосовуватися для задання топологій систем, але вони не можуть задавати топології, що містять петлі – контури, що складаються лише з одного елемента. Наприклад, скласти матрицю інциденції для топології (рис.1.1.) є проблематичним. Крім того, елементи таких матриць можуть приймати одне із трьох значень +1,1,0, а тому для перетворення матриць інциденції з метою аналізу заданих топологій потрібно застосовувати або звичайні алгебраїчні операції, які є більш трудомісткі, ніж логічні операції двійкової алгебри логіки, або операції трійкової алгебри логіки, які хоч менш трудомісткі від звичайних операцій, але складніші від операційбулевої алгебри. З цих міркувань монографії для задання топологой систем застосовуються лише матриці суміжності.
Перевага застосування матриці суміжностей полягає у зручності представлення, опрацювання та зберігання в комп’ютерах топологій з довільною кількістю елементів. Такі матриці в комп’ютерах записуються як масиви або списки зв’язності, що очевидно є для них найбільш природним представленням. Враховуючи також і те, що елементи матриць суміжностей приймають тільки два значення, то над ними зручно застосовувати менш трудомісткі операції алгебри логіки та інші спеціальні для аналізу топології систем.
Єдиним, але суттєвим, недоліком матричних способів задання топологій є низька наочність. Тому, для виведення на екран монітора результатів аналізу топологій у відповідних програмах необхіджно передбачити перетворення матриць у графи.
Похожие работы
... іжності мережі. Найбільш прийнятним в плані простоти алгоритмізації операторним перетворенням матриці, шо відповідає умові самоприв'язки елемента до структури матриці, є піднесення її до степеня. Матриця в загальному випадку описує певний простір, просторову множину, в даному випадку виміру N. Далі визначимо, що саме описує вхідна матриця суміжності. Оскільки матриця представляє собою логічну ...
... of normal functors // Міжнародний конгрес математиків "International Mediterranean Congress of Mathematics", м. Альмерія, 2005, тези доповідей. АНОТАЦІЯ Кожан Р.В. Категорні властивості просторів ймовірнісних мір та гіперпросторів включення. – Рукопис. Дисертація на здобуття наукового ступеня кандидата фізико-математичних наук за спеціальністю 01.01.01 – математичний аналіз – Львівський ...
... необхідних заходів [11]. У додатку А наведена блок-схема аналізу комерційного запиту та укладання угод на поставку продукції. інформація правовий технологія 1.3 Вихідна інформація ТОВ «Насоселектромаш» Вихідною інформацією підприємства ТОВ «Насоселектромаш» є результати роботи усіх його відділів: - підписані контракти з контрагентами у результаті роботи з отриманими запитами; - журнали ...
... за якими вибирають типорозмір придатного корпуса з числа нормалізованих. Типорозмір №8. Довжина l=16мм Ширина b=12 мм 16х12 мм Остаточні розміри плати встановлюють після проектування топологічної схеми на етапі розробки конструкції ІС. 7. Розробка топології мікросхеми Bибip форми i розміщення плівкових елементів i навісних компонентів проводить на основі комутаційної схеми, даних про ...

0 комментариев