АЛГОРИТМ РІШЕННЯ ЕКСТРЕМАЛЬНИХ ЗАДАЧ МЕТОДОМ ЯКОБІ

4. АЛГОРИТМ РІШЕННЯ ЕКСТРЕМАЛЬНИХ ЗАДАЧ МЕТОДОМ ЯКОБІ

Розглянемо наступну задачу:

 мінімізувати

при обмеженнях g(X) =0,

де X=(x₁,x₂,…,x_n),g=(g₁,g₂,…,g_m)^T...

Функції  і  i=1,2,..., m, передбачаються двічі безупинно дифференційними.

Ідея використання приведеного градієнта для рішення сформульованої вище задачі полягає в тім, щоб знайти аналітичне вираження для перших часток похідних функції  у всіх крапках, що задовольняють обмеженню g(X) =0. При цьому стаціонарними будуть крапки, у яких зазначені частки похідні звертаються в нуль. Для класифікації стаціонарних крапок можна користатися достатніми умовами існування екстремумів.

З теореми Тейлора випливає, що для крапки  з припустимої околиці крапки X можна записати наступні формули:

При  маємо

Тому що g(X)=0, те =0 у припустимій області. Звідси

Отримана система містить (m+1) рівнянь з (n+1) невідомими, котрими є  і . Невідому величину  можна визначити, якщо знайдений вектор . Це означає, що в нас мається m рівнянь з n невідомими.

Якщо m>n то принаймні (m-n) рівнянь виявляються надлишковими. Після усунення надмірності кількість незалежних рівнянь у системі стає рівним m<n. У випадку коли m=n рішення тривіальне: =0. При цьому крапка X не має припустимої околиці, і, отже, простір рішень складається з єдиної крапки. Така ситуація не представляє інтересу. Випадок, що залишився, коли m<n, необхідно розглянути докладно. Нехай X(Y,Z), де Y=(y₁,y₂,…,y_m)і Z=(z₁,z₂,…,z_n-m)є відповідно залежний і незалежний перемінний, утворюючий вектор Х. У нових позначеннях градієнти функцій  і g мають наступний вид:

Уведемо визначення двох матриць:

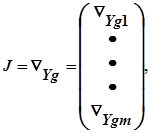
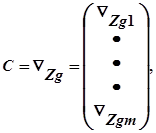
Матрицю J_mxm: називають матрицею Якобі, а C_{mx (n-m)} -матрицею керування. Передбачається, що матриця Якобі J невирождена. Цей факт завжди має місце, оскільки m рівнянь незалежні по визначенню. Отже, компоненти вектора J можна вибрати серед компонентів X таким чином, що матриця J виявиться невирожденою.

Використовуючи дані вище визначення, перепишемо вихідну систему рівнянь з невідомими  й  у наступному виді:

Тому що матриця J— невирождена, існує зворотна матриця J^-1. Отже,

Ці рівняння визначають  як функцію  (нагадаємо, що Z є вектором незалежних перемінних). Заміна в рівнянні  дозволяє виразити через :

 З цього рівняння випливає, що диференціювання функції  по векторі незалежних перемінних Z дає формулу:

де -приведений градієнт функції. Вектор (Y,Z) повинний звертатися в нуль у стаціонарних крапках.

Достатні умови наявності єкстремуми в стаціонарній крапці аналогічні умовам, представленим у розділі. 1.1. У цьому випадку елементи матриці Гессе відповідають компонентам вектора незалежних перемінних Z і є приведеними другими похідними, які можна обчислити, скориставшись рівністю:

Вектор  задає i-ю рядок (приведеної) матриці Гессе. Помітимо, що W є функцією Y, а Y— функцією Z; при цьому

Таким чином, при обчисленні частинної похідної по z_i, варто застосувати до компонентів W правило диференціювання складної функції. Це означає, що

5. ІНДИВІДУАЛЬНЕ ЗАВДАННЯ

 

5.1. Постановка задачі.

 

 Розглядається наступна задача:

максимізувати X=x1²+2x2²+10x3²+5x1x2,

 при

 g1 (X)=x1+x2+3x2x3-5=0

 g2 (X)=x1²+5x1x2+x3x2+x3²-7=0

Застосувати метод Якобі для перебування дс (х) у припустимій околиці припустимої крапки X₀ (1,1,1). Припустити, що зазначена околиця визначається умовою  

5.2. Рішення задачі

Нехай Y=(X₂,X₃), Z=X₃ має:

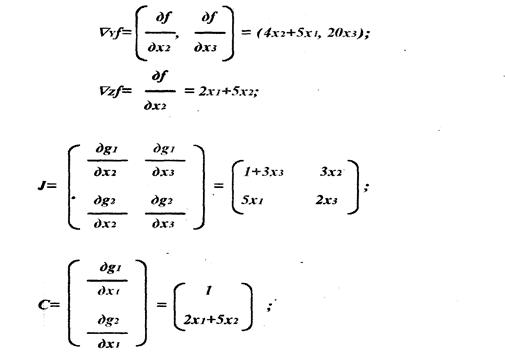
Для того щоб одержати оцінку збільшення  в припустимій околиці припустимої крапки X₀ (1,1,1), викликаного малою зміною , варто обчислити

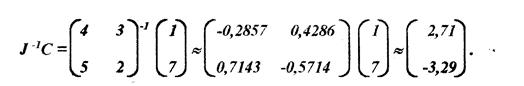
Отже

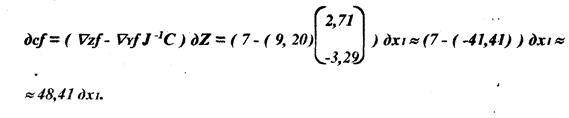
Тому що:

Якщо задана величина зміни  незалежної перемінний Х₁, то припустимі значення  і  залежних перемінних Х₂ і Х₃ визначаються відповідно до формули

 .

При  одержуємо

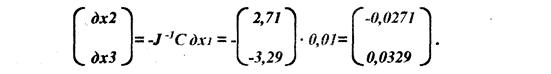
Для перевірки точності отриманої вище оцінки  обчислимо іншим способом:

Знайдемо (X) і (Х₀+ ).

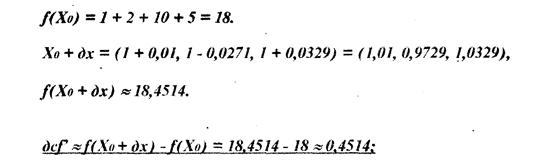
Отримане значення не збігається з величиною обчисленої вище. Розходження між двома результатами (0,4841 і 0,4514) є наслідком лінійної апроксимації, що фігурує в задачі нелінійних функцій в околиці крапки Х₀. Тому використану вище формулу можна застосовувати лише у випадках, коли відхилення від крапки Х₀ малі.