Навигация
Аппроксимация функции с использованием нейронных сетей
Министерство образования и науки Российской Федерации Федеральное агентство по образованию
Амурский гуманитарно-педагогический государственный университет
Физико-математический факультет
ЛАБОРАТОРНАЯ РАБОТА №1
по дисциплине «Искусственные нейронные сети» на тему «Аппроксимация функции с использованием нейронных сетей»
2007
Содержание
Введение
1 Теоретические сведения
2 Методика выполнения лабораторной работы
3 Контрольные вопросы
Заключение
Список использованных источников
Введение
Цель лабораторной работы:
Научиться использовать нейронные сети для аппроксимации функции.
Задание: В среде Matlab необходимо построить и обучить нейронную сеть для аппроксимации таблично заданной функции ![]() , i=1,20. Разработать программу, которая реализует нейросетевой алгоритм аппроксимации и выводит результаты аппроксимации в виде графиков.
, i=1,20. Разработать программу, которая реализует нейросетевой алгоритм аппроксимации и выводит результаты аппроксимации в виде графиков.
1 Теоретические сведения
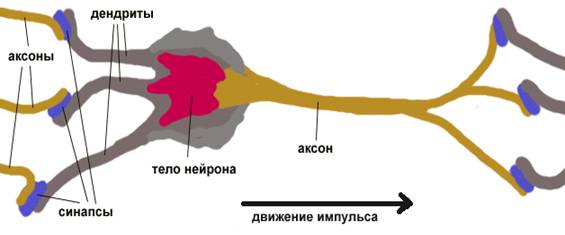
Понятие искусственного нейрона и искусственных нейронных сетей. Под искусственными нейронными сетями подразумеваются вычислительные структуры, которые моделируют простые биологические процессы, обычно ассоциируемые с процессами человеческого мозга. Они представляют собой распределенные и параллельные системы, способные к адаптивному обучению путем анализа положительных и отрицательных воздействий. Элементарным преобразователем в данных сетях является искусственный нейрон или просто нейрон, названный так по аналогии с биологическим прототипом. К настоящему времени предложено и изучено большое количество моделей нейроноподобных элементов и нейронных сетей.
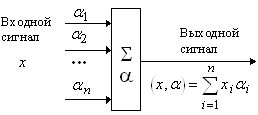
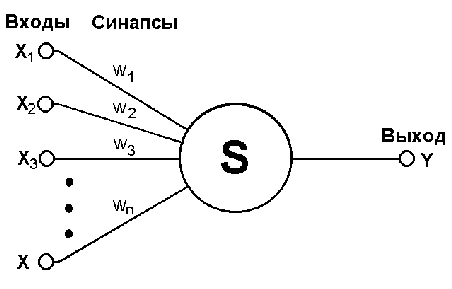
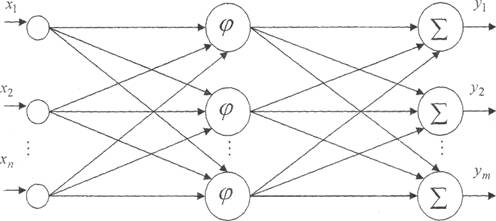
Нейрон является составной частью нейронной сети. Общая структура:
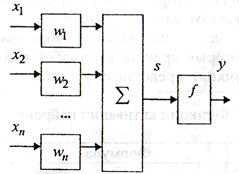
Он состоит из элементов трех типов: умножителей (синапсов), сумматора и нелинейного преобразователя. Синапсы осуществляют связь между нейронами, умножают входной сигнал на число, характеризующее силу связи (вес синапса). Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента – выхода сумматора. Эта функция называется функцией активации или передаточной функцией нейрона. Нейрон в целом реализует скалярную функцию векторного аргумента.
Математическая модель нейрона:
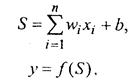
где S – результат суммирования (sum); ω(i) – вес (weight) синапса, i=1,n; x – компонент входного вектора (входной сигнал), i=1,n; b – значение смещения (bias); n – число входов нейрона; у – выходной сигнал нейрона; f – нелинейное преобразование (функция активации).
В общем случае входной сигнал, весовые коэффициенты и смещение могут принимать действительные значения, а во многих практических задачах – лишь некоторые фиксированные значения. Выход у определяется видом функции активации и может быть как действительным, так и целым.
Синаптические связи с положительными весами называют возбуждающими, с отрицательными – тормозящими. Описанный вычислительный элемент можно считать упрощенной математической моделью биологических нейронов. Чтобы подчеркнуть различие нейронов биологических и искусственных, вторые иногда называют нейроподобными элементами, или формальными нейронами.
На входной сигнал S нелинейный преобразователь отвечает выходным сигналом f(S), который представляет собой выход у нейрона.
Примеры активационных функций:


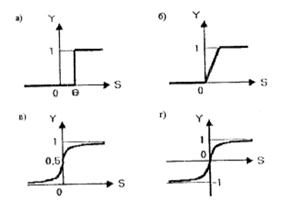
Примеры активационных функций:
а) функция единичного скачка; б) линейный порог (гистерезис); в) сигмоид (логистическая функция); г) сигмоид (гиперболический тангенс).
Одной из наиболее распространенных является нелинейная функция активации, так называемая логистическая функция, или сигмоид (функция S – образного вида):
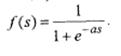
При уменьшении а сигмоид становится более пологим, в пределе при а=0 вырождаясь в горизонтальную линию на уровне 0,5, при увеличении а сигмоид приближается к виду единичного скачка с порогом θ. Очевидно, что выходное значение нейрона лежит в диапазоне (0,1). Одно из ценных свойств сигмоидальной функции – простое выражение ее производной:
![]()
Сигмоидальная функция дифференцируема на всей оси абсцисс. Она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.
Похожие работы
... сети, позволяющая реализовать автоматическое изменение числа нейронов в зависимости от потребностей задачи, позволяет не только исследовать, но и контролировать процесс воспитания психологической интуиции искусственных нейронных сетей. - Впервые применена выборочная константа Липшица для оценки необходимой для решения конкретной задачи структуры нейронной сети. Практическая значимость ...
... экспертных систем (А. Батуро), а также лекции проф. А.Н. Горбаня по нейронным сетям. Приложение 1. Плакаты для защиты диплома. ТЕХНОЛОГИЯ ИЗВЛЕЧЕНИЯ ЗНАНИЙ ИЗ НЕЙРОННЫХ СЕТЕЙ: ¨ АПРОБАЦИЯ, ¨ ПРОЕКТИРОВАНИЕ ПО, ¨ ИСПОЛЬЗОВАНИЕ В ПСИХОЛИНГВИСТИКЕ ЦЕЛЬ РАБОТЫ ¨ апробация гибкой технологии извлечения ...
... . Если же задача не может быть сведена ни к одному из известных классов, разработчику приходится решать задачу синтеза новой конфигурации. Проблема синтеза искусственной нейронной сети сильно зависит от задачи, дать общие подробные рекомендации затруднительно. В большинстве случаев оптимальный вариант искусственной нейронной сети получается опытным путем. Искусственные нейронные сети могут быть ...
... : данные сети обладают плохими экстраполирующими свойствами и получаются весьма громоздкими при большой размерности вектора входов. На рис. 1 представлена структурная схема нейронной сети с радиальными базисными функциями. Нейронная сеть радиальных базисных функций содержит в наиболее простой форме три слоя: обычный входной слой, выполняющий распределение данных образца для первого слоя весов; ...

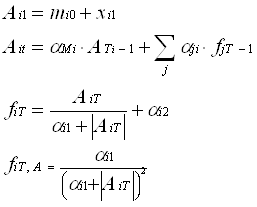
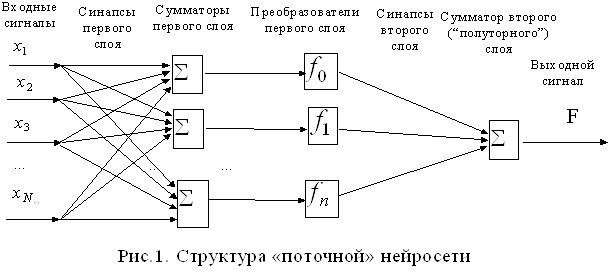


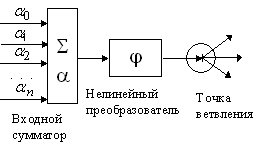

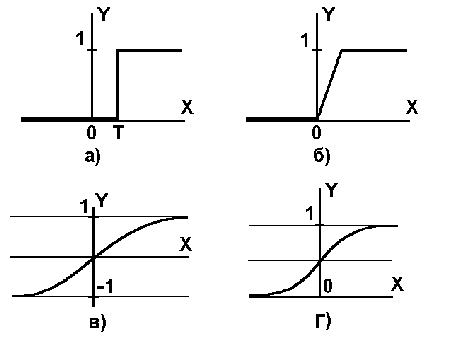
0 комментариев