Навигация
Выявление основной тенденции ряда. Аналитическое выравнивание
54485
знаков
18
таблиц
12
изображений
3.2. Выявление основной тенденции ряда. Аналитическое выравнивание
Аналитическое выравнивание ряда динамики имеет задачу найти плавную линию развития данного явления, характеризующую основную тенденцию ее динамики.
Проведем аналитическое выравнивание по уравнению прямой у=a+bt.
Для этого необходимо решить систему уравнений
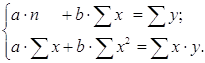
| t | Yt | t*t | y*t |
| 1 | 365 | 1 | 365 |
| 2 | 320 | 4 | 640 |
| 3 | 295 | 9 | 885 |
| 4 | 310 | 16 | 1240 |
| 5 | 334 | 25 | 1670 |
| 6 | 385 | 36 | 2310 |
| 7 | 391 | 49 | 2737 |
| 8 | 362 | 64 | 2896 |
| 9 | 310 | 81 | 2790 |
| 10 | 290 | 100 | 2900 |
| 11 | 320 | 121 | 3520 |
| 12 | 330 | 144 | 3960 |
| 13 | 370 | 169 | 4810 |
| 14 | 340 | 196 | 4760 |
| 15 | 310 | 225 | 4650 |
| 16 | 280 | 256 | 4480 |
| 17 | 320 | 289 | 5440 |
| 18 | 350 | 324 | 6300 |
| 19 | 380 | 361 | 7220 |
| 20 | 402 | 400 | 8040 |
| 21 | 365 | 441 | 7665 |
| 22 | 296 | 484 | 6512 |
| 23 | 320 | 529 | 7360 |
| 24 | 340 | 576 | 8160 |
| сумма | 8085 | 4900 | 101310 |
Подставим данные в уравнение
a=328.12 b=0.69
Уравнение регрессии:
=328,12+0,69t
Проведем оценку параметров на типичность по формулам:
=28,36
=5,59
Это значит уравнение регресии значимо в целом.
=7,12
=13,24
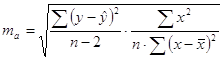=23,24
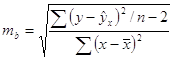=0,654
=0,214
=4,83
=2,36
Отвергается гипотеза о случайной природе оцениваемых характеристик и подтверждается их статистическая значимость и надежность.
Расчитаем среднюю и предельную ошибки.
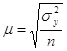
Построим график и тренд аналитического выравнивания
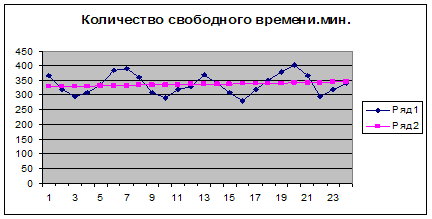
3.3.Метод скользящих средних
Отобразим графически наш ряд, чтобы определить аддитивную или мультипликативную модель использовать.
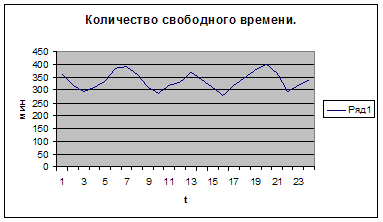
Проанализировав график можно сделать вывод о том ,что нам подходит аддитивная модель, т.к. количество свободного времени не увеличивается от цикла к циклу. Для того, чтобы определить период колебаний построим автокорреляционную функцию. Для этого определим коэффициент автокорреляции для каждого уровня, который рассчитывается по формуле: 
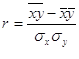
По полученным данным построим таблицу
Таблица 4
| r1 | r2 | r3 | r4 | r5 | r6 | r7 | r8 | r9 |
| 0,099 | -0,061 | 0,311 | 0,827 | -0,056 | 0,860 | 0,205 | 0,734 | -0,270 |
| r10 | r11 | r12 | r13 | r14 | r15 | r16 | r17 | r18 |
| -0,441 | -0,061 | 0,079 | -0,048 | 0,249 | 0,662 | -0,045 | 0,688 | 0,420 |
Т.к. r6 оказался самым высоким, то ряд содержит циклические колебания с периодичностью в 6 месяцев.
| t | y | итого за 6 месяцев. | скользящая сред. За 6 м. | Центриров. скользящая средняя | Оценка сезонной компоненты |
| 1 | 365 | - | - | - | - |
| 2 | 320 | 2009 | 334,8333 | - | - |
| 3 | 295 | 2035 | 339,1667 | 337 | -42 |
| 4 | 310 | 2077 | 346,1667 | 342,6667 | -32,6667 |
| 5 | 334 | 2092 | 348,6667 | 347,4167 | -13,4167 |
| 6 | 385 | 2072 | 345,3333 | 347 | 38 |
| 7 | 391 | 2058 | 343 | 344,1667 | 46,83333 |
| 8 | 362 | 2003 | 333,8333 | 338,4167 | 23,58333 |
| 9 | 310 | 1982 | 330,3333 | 332,0833 | -22,0833 |
| 10 | 290 | 1960 | 326,6667 | 328,5 | -38,5 |
| 11 | 320 | 1960 | 326,6667 | 326,6667 | -6,66667 |
| 12 | 330 | 1950 | 325 | 325,8333 | 4,166667 |
| 13 | 370 | 1950 | 325 | 325 | 45 |
| 14 | 340 | 1970 | 328,3333 | 326,6667 | 13,33333 |
| 15 | 310 | 1980 | 330 | 329,1667 | -19,1667 |
| 16 | 280 | 2042 | 340,3333 | 335,1667 | -55,1667 |
| 17 | 320 | 2097 | 349,5 | 344,9167 | -24,9167 |
| 18 | 350 | 2113 | 352,1667 | 350,8333 | -0,83333 |
| 19 | 380 | 2113 | 352,1667 | 352,1667 | 27,83333 |
| 20 | 402 | 2103 | 350,5 | 351,3333 | 50,66667 |
| 21 | 365 | - | - | - | - |
| 22 | 296 | - | - | - | - |
| 23 | 320 | - | - | - | - |
| 24 | 340 | - | - | - | - |
Чтобы определить скользящие средние использовались следующие формулы:
Чтобы определить центрированные средние использовались следующие формулы:
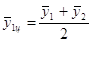
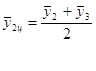и т.д.
Оценки сезонных компонент =
Транспонируем данные оценок сезонных компонент и представим их в следующей таблице.
| - | - | -42 | -32,6667 | -13,4167 | 38 | |
| 46,83333 | 23,58333 | -22,0833 | -38,5 | -6,66667 | 4,166667 | |
| 45 | 13,33333 | -19,1667 | -55,1667 | -24,9167 | -0,83333 | |
| 27,83333 | 50,66667 | - | - | - | - | |
| Si | 39,88889 | 29,19444 | -27,75 | -42,1111 | -15 | 13,77778 |
| Sk | 40,22222 | 29,52778 | -27,4167 | -41,7778 | -14,6667 | 14,11111 |
Si= сумме значений по столбцам. Суммарное значение Si должно равняться 0. В нашем случае сумма Si=-2.
Найдем коэффициент корректировки К=
К=-0,3333
Sскор=Si-К.
скор=0
Находим уравнение регрессии, решив систему уравнений, относительно a и b.
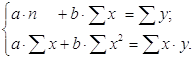
Уравнение регрессии:=328,12+0,69t
Проведем оценку параметров на типичность по формулам:
=28,36
=5,59
Это значит уравнение регресии значимо в целом.
=7,12
=13,24
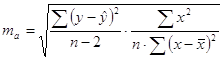=23,24
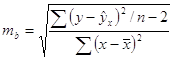=0,654
=0,214
=4,83
=2,36
Отвергается гипотеза о случайной природе оцениваемых характеристик и подтверждается их статистическая значимость и надежность. Е=У-Уt
| t | Yt | S | Y-S | T | T+S | E |
| 1 | 365 | 40,22222 | 324,7778 | 328,8478 | 369,07 | 36,1522 |
| 2 | 320 | 29,52778 | 290,4722 | 329,5456 | 359,0734 | -9,5456 |
| 3 | 295 | -27,4167 | 322,4167 | 330,2434 | 302,8267 | -35,2434 |
| 4 | 310 | -41,7778 | 351,7778 | 330,9412 | 289,1634 | -20,9412 |
| 5 | 334 | -14,6667 | 348,6667 | 331,639 | 316,9723 | 2,361 |
| 6 | 385 | 14,11111 | 370,8889 | 332,3368 | 346,4479 | 52,6632 |
| 7 | 391 | 40,22222 | 350,7778 | 333,0346 | 373,2568 | 57,9654 |
| 8 | 362 | 29,52778 | 332,4722 | 333,7324 | 363,2602 | 28,2676 |
| 9 | 310 | -27,4167 | 337,4167 | 334,4302 | 307,0135 | -24,4302 |
| 10 | 290 | -41,7778 | 331,7778 | 335,128 | 293,3502 | -45,128 |
| 11 | 320 | -14,6667 | 334,6667 | 335,8258 | 321,1591 | -15,8258 |
| 12 | 330 | 14,11111 | 315,8889 | 336,5236 | 350,6347 | -6,5236 |
| 13 | 370 | 40,22222 | 329,7778 | 337,2214 | 377,4436 | 32,7786 |
| 14 | 340 | 29,52778 | 310,4722 | 337,9192 | 367,447 | 2,0808 |
| 15 | 310 | -27,4167 | 337,4167 | 338,617 | 311,2003 | -28,617 |
| 16 | 280 | -41,7778 | 321,7778 | 339,3148 | 297,537 | -59,3148 |
| 17 | 320 | -14,6667 | 334,6667 | 340,0126 | 325,3459 | -20,0126 |
| 18 | 350 | 14,11111 | 335,8889 | 340,7104 | 354,8215 | 9,2896 |
| 19 | 380 | 40,22222 | 339,7778 | 341,4082 | 381,6304 | 38,5918 |
| 20 | 402 | 29,52778 | 372,4722 | 342,106 | 371,6338 | 59,894 |
| 21 | 365 | -27,4167 | 392,4167 | 342,8038 | 315,3871 | 22,1962 |
| 22 | 296 | -41,7778 | 337,7778 | 343,5016 | 301,7238 | -47,5016 |
| 23 | 320 | -14,6667 | 334,6667 | 344,1994 | 329,5327 | -24,1994 |
| 24 | 340 | 14,11111 | 325,8889 | 344,8972 | 359,0083 | -4,8972 |
Количество свободного времени в мин. за 2006-2007 гг..
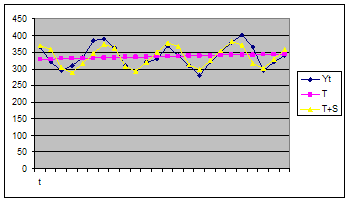
Произведем прогнозирование на 6 месяцев.
| t | Т | S | Т+S |
| 25 | 345,595 | 40,22222 | 385,8172 |
| 26 | 346,2928 | 29,52778 | 375,8206 |
| 27 | 346,9906 | -27,4167 | 319,5739 |
| 28 | 347,6884 | -41,7778 | 305,9106 |
| 29 | 348,3862 | -14,6667 | 333,7195 |
| 30 | 349,084 | 14,11111 | 363,1951 |
Похожие работы
... , воспитание активного ценностного отношения людей к образцам высокой духовной культуры, ее всестороннее усвоение. 2. Роль организации свободного времени в развитии персонала 2.1 Социальная трудовая среда Человеческий труд, с социологической точки зрения определяемый как целенаправленная человеческая деятельность, в процессе которой он создает материальные и духовные ценности для ...
... планировка отдельного помещения, комплекса сооружений, их величина форма и т.д. могут экономить время человека или, наоборот, способствовать его нерациональному расходованию. Большинство социологов рассматривают использование свободного времени в двух аспектах: как физическую деятельность, связанную с физическим развитием, и как духовную, направленную на духовное развитие человека. При этом одна ...
... в этой стране методологии его расчёта. В настоящее время в большинстве стран используется статистический метод определения черты бедности, который предполагает установление прожиточного минимума исходя из принятого стандарта потребления на уровне 40-60% фактически сложившихся среднедушевых доходов населения. Данный метод используется, как правило, странами со стабильной динамикой развития ...
... ; - изменение среднедушевого дохода (цены товара) за истекший период. Выборочные бюджетные обследования в России являются важнейшим источником статистической информации для изучения региональных различных в уровне жизни населения. Материалы таких обследований позволяют анализировать уровень жизни низкодоходных групп населения, а также используются при разработке бюджетов прожиточного ...
0 комментариев