Навигация
8. Качество информации
Возможность и эффективность использования информации обусловливаются такими основными ее потребительскими показателями качества, как репрезентативность, содержательность, достаточность, доступность, актуальность, своевременность, точность, достоверность, устойчивость. Репрезентативность информации связано с правильностью ее отбора и формирования в целях адекватного отражения свойств объекта. Важнейшее значение имеют: правильность концепции, на базе которой сформулировано исходное понятие и обоснованность отбора существенных признаков и связей отображаемого явления.
2. Измерение информации
Мощность информационного сигнала, также как и вес носителя информации не могут служить оценкой количества информации, переносимой сигналом.
Истрепанная книжка, если в ней нет вырванных страниц, несет для вас ровно столько же информации, сколько такая же новая.
2.1. Измерение информации в быту (информация как новизна)
Вы получили какое-то сообщение. В этом сообщении содержится какое-то количество информации. Как оценить, сколько информации вы получили? Другими словами, как измерить информацию? Можно ли сказать, что чем больше статья, тем больше информации она содержит?
Разные люди, получившие одно и тоже сообщение, по-разному оценивают количество информации, содержащееся в нем. Это происходит оттого, что знания людей об этих событиях, явлениях до получения сообщения были различными. Поэтому те, кто знал об этом мало, сочтут, что получили много информации, те же, кто знал больше, чем написано в статье, скажут, что информации не получили вовсе. Количество информации в сообщении зависит от того, насколько важно сообщение для получателя. При таком подходе непонятно, по каким критериям можно ввести единицу измерения информации. С точки зрения информации как новизны можно оценить количество информации, содержащейся в научном открытии, музыкальном стиле, новой теории общественного развития.
2.2. Измерение информации в технике
В технике информацией считается любая хранящаяся, обрабатываемая или передаваемая последовательность знаков, символов. В технике под количеством информации понимают количество кодируемых, передаваемых или хранимых символов.
Определить понятие «количество информации» сложно. В решении этой проблемы существуют два основных подхода. Исторически они возникли почти одновременно. В конце 40-х годов XX века Клод Шеннон развил вероятностный подход к измерению количества информации, работы по созданию ЭВМ привели к «объемному» подходу. В технике используют простой способ определения количества информации, названный объемным, основанный на подсчете числа символов в сообщении, не связан с его длиной и не учитывает содержания.
Пример: собака – 6 символов, dog – 3 символа.
Человеку привычно работать с символами, а компьютеру - с кодами. Каждый символ кодируется двоичным кодом, длиной в 8 знаков (восьмибитный код).
Прежде чем измерить информацию в битах, вы определяете количество символов в этом сообщении. Каждый символ не случайно кодируется 8-битным кодом. Для удобства введена более "крупная" единица информации в технике – байт, с помощью которой легче подсчитать количество информации в техническом сообщении - оно совпадает с количеством символов в нем.
В вычислительной технике: бит (binary digit) - двоичный знак двоичного алфавита {0, 1}, минимальная единица измерения информации.
Байт (byte) - единица количества информации в системе СИ. Байт - восьмиразрядный двоичный код, с помощью которого можно представить один символ.
Единицы измерения информации в вычислительной технике:
| Бит | Элементарная единица информации |
| Байт (б) | 8 бит |
| Килобайт (Кбайт) | 210 байт = 1024 байт |
| Мегабайт (Мбайт) | 210 Кбайт = 220 байт |
| Гигабайт (Гбайт) | 210 Мбайт = 230 байт |
| Терабайт (Тбайт) | 1024 Гбайт = 240 байт |
| Петабайт (Пбайт) | 1024 Тбайт = 250 байт |
| Эксабайт (Эбайт) | 1024 Пбайт = 260 байт |
Информационный объем сообщения (информационная емкость сообщения) - количество информации в сообщении, измеренное в битах, байтах, производных единицах (Кб, Мб и т.д.) [2].
Длина сообщения зависит от числа различных символов, употребляемых для записи сообщения. Например, слово "мир" в русском алфавите записывается тремя знаками, в английском - пятью (peace), а в КОИ-8 - двадцатью четырьмя битами (111011011110100111110010).
2.3. Измерение информации в теории информации (информация как снятая неопределенность)
В теории информации количеством информации называют числовую характеристику сигнала, не зависящую от его формы и содержания и характеризующую неопределенность, которая исчезает после получения сообщения в виде данного сигнала - в этом случае количество информации зависит от вероятности получения сообщения о том или ином событии.
Для абсолютно достоверного события (событие обязательно произойдет, поэтому его вероятность равна 1) количество вероятности в сообщении о нем равно 0. Чем вероятнее событие, тем больше информации о нем несет сообщение.
Лишь при равновероятных ответах ответ "да" или "нет" несет 1 бит информации. Оценка количества информации основывается на законах теории информации. Сообщение имеет ценность, несет информацию, когда мы узнаем и понимаем смысл данного сообщения.
Какое количество информации содержится, к примеру, в тексте романа "Война и мир", в фресках Рафаэля или в генетическом коде человека? Ответа на эти вопросы наука не даёт и, по всей вероятности, даст не скоро.
А возможно ли объективно измерить количество информации? Важнейшим результатом теории информации является вывод: в определенных, весьма широких условиях можно пренебречь качественными особенностями информации, выразить её количество числом, а также сравнить количество информации, содержащейся в различных группах данных.
Теория информации как самостоятельная научная дисциплина была основана Клодом Шенноном в конце 40-х годов 20 века. Предложенная им теория основывалась на фундаментальном понятии количественной меры неопределенности – энтропии и связанного с нею понятия количества информации.
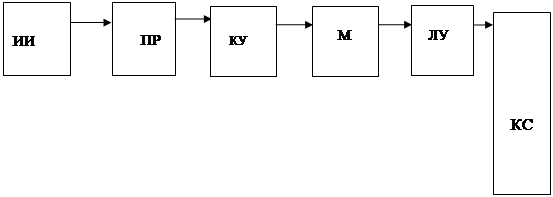
Сигнал – это материальный носитель информации (предмет, явление, процесс) в пространстве и во времени. Любой сигнал неразрывно связан с определенной системой, которая является системой связи или системой передачи информации и состоит из следующих модулей: источник, передатчик, канал связи, приемник и адресат. Источник информации задает некоторое множество сообщений. Генерация определенного сообщения заключается в выборе его из множества всех возможных. Сообщения бывают дискретными и непрерывными. Светофор или передача сообщения с помощью азбуки Морзе – примеры дискретного сигнала.
Особым видом сигналов являются знаки, которые в отличие от сигналов естественного происхождения создаются самоорганизующимися системами и предназначаются для передачи и хранения информации. Есть знаки, входящие в четко организованную систему, и внесистемные знаки. Например: знаки дорожного движения, система цветов светофора, музыка, речь и языки, как естественные, так и искусственные. Внесистемные знаки – это или остатки некогда существовавших знаковых систем, или знаки, созданные временно, обычно в небольших коллективах людей. Например, языки жестов и поз.
В теории информации и кодировании принят энтропийный подход к измерению информации, который основан на том, что факт получения информации всегда связан с уменьшением разнообразия или неопределенности (энтропии) системы. Неопределенность может быть интерпретирована в смысле того, насколько мало известно наблюдателю о данной системе, энтропия системы снизилась, так как для наблюдателя система стала более упорядоченной.
При энтропийном подходе под информацией понимается количественная величина исчезнувшей в ходе какого-либо процесса (испытания, измерения и т.д.) неопределенности. При этом в качестве меры неопределенности вводится энтропия [1].
Энтропия – мера внутренней неупорядоченности информационной системы.
Энтропия увеличивается при хаотическом распределении информационных ресурсов и уменьшается при их упорядочении.
На основе понятий энтропии и количества информации в теории информации введены важные характеристики сигналов и информационных систем:
скорость создания информации;
скорость передачи информации;
избыточность;
пропускная способность каналов связи.
Одним из самых замечательных результатов теории информации является доказательство, что при любых помехах и шумах можно обеспечить передачу информации без потерь.
Первая теорема Шеннона гласит, что при скорости создания информации меньшей пропускной способности канала можно передавать информацию со сколь угодно малой вероятностью ошибок, несмотря на шумы.
Шеннон сформулировал энтропию как меру хаоса в противовес количеству информации как меры упорядоченности структур.
Рассмотрим некоторую сложную систему и проследим ее эволюцию. Пусть эта система представляет собой находящийся в сосуде газ, состоящий из огромного числа беспорядочно движущихся молекул. Мы не знаем точного положения и скорости в каждый момент времени каждой частицы газа, но нам известны макропараметры: давление, объем, температура и состав газа. Фактически мы должны рассчитать число способов, которыми можно осуществить внутренние перестройки в системе, чтобы наблюдатель не заметил изменений макросостояния системы. При этом предполагается неотличимость атомов друг от друга.
Если в системе, состоящей из одного атома, произошло его энергетическое возбуждение, нам это может стать известно по значению температуры. При этом возможно только одно распределение возбуждения в системе равному единице. Энтропия связана с распределением следующим образом: ![]() . В нашем случае
. В нашем случае ![]() , а значит, система обладает нулевой энтропией.
, а значит, система обладает нулевой энтропией.
В системе из ста атомов, распределение возбуждения может быть осуществлено ста способами, т.е. ![]() ,
, ![]() . Энтропия системы выросла и стала хаотичной, поскольку мы не знаем, где находится в каждый момент возбужденный атом.
. Энтропия системы выросла и стала хаотичной, поскольку мы не знаем, где находится в каждый момент возбужденный атом.
Принято считать, что любая система стремится к состоянию равновесия, т.е. растет энтропия системы. Однако второе начало термодинамики (закон сохранения энтропии и информации) требует компенсировать рост энтропии. Информация и является средством компенсации.
В настоящее время получили распространение подходы к определению понятия "количество информации", основанные на том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле её новизны или, иначе, уменьшения неопределённости наших знаний об объекте.
Р. Хартли предложил в качестве меры неопределенности логарифм от числа возможностей, т.е. процесс получения информации рассматривает как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определяет как двоичный логарифм N: ![]() - формула Хартли.
- формула Хартли.
Обычно количество информации представляется в виде: ![]() , где m - число возможных выборов. Тогда стандартной единицей количества информации будет выбор из двух возможностей. Такая единица получила наименование бит и представляется одним символом двоичного алфавита: 0 или 1.
, где m - число возможных выборов. Тогда стандартной единицей количества информации будет выбор из двух возможностей. Такая единица получила наименование бит и представляется одним символом двоичного алфавита: 0 или 1.
Пример: нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: ![]() .Т. е. сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единиц информации.
.Т. е. сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единиц информации.
Другие примеры равновероятных сообщений: при бросании монеты: "выпала решка", "выпал орел"; на странице книги: "количество букв чётное", "количество букв нечётное".
В некоторых случаях, когда однозначно нельзя ответить на вопросы распределения вероятности, для определения количества информации уже нельзя использовать формулу Хартли.
Пример: являются ли равновероятными сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина". Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь.
Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.
Формула Шеннона:
![]() ,
,
где рi - вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.
Если вероятности ![]() равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.
равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.
3. Кодирование информации
Кодирование информации - это процесс формирования определенного представления информации [3].
В более узком смысле под термином кодирование часто понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки.
Компьютер может обрабатывать только информацию, представленную в числовой форме. Вся другая информация (звуки, изображения, показания приборов и т.д.) для обработки на компьютере должна быть преобразована в числовую форму. Чтобы перевести в числовую форму музыкальный звук, можно через небольшие промежутки времени измерять интенсивность звука на определенных частотах, представляя результаты каждого измерения в числовой форме. Аналогичным образом можно обрабатывать текстовую информацию. При вводе в компьютер каждая буква кодируется определенным числом, при выводе на внешние устройства для восприятия человеком по этим числам строятся изображения букв. Соответствие между набором букв и числами называется кодировкой символов.
Одну и ту же информацию можно выразить разными способами. Например, каким образом вы можете сообщить об опасности?
Если на вас напали, вы просто можете крикнуть: «Караул!!! »
Если прибор находится под высоким напряжением, то требуется оставить предупреждающий знак;
На оживленном перекрестке регулировщик помогает избежать аварии с помощью жестов.
В театре пантомимы вся информация передается только с помощью мимики и жестов.
Если ваш корабль тонет, то вы передаете сигнал «SOS».
На флоте используют семафорную и флажковую сигнализацию.
В каждом из этих примеров мы должны знать правила, по которым можно отобразить информацию об опасности тем или иным способом.
Правила, по которым можно отобразить информацию тем или иным способом, называются кодом.
Обычно каждый образ при кодировании представлен отдельным знаком.
Знак – это элемент конечного множества, отличных друг от друга элементов. Знак вместе его смыслом называется символом. Набор знаков, в котором определен их порядок, называется алфавитом. Мощность алфавита - количество используемых в нем символов.
Существует множество алфавитов: алфавит кириллических букв (А, Б, В, Г, Д, …); алфавит латинских букв (A, B, C, D, …); алфавит десятичных цифр (1, 2, 3, 4,…,9, 0); алфавит знаков зодиака и др.
Имеются, однако, наборы знаков, для которых нет какого-то общепринятого порядка: набор знаков азбуки Брайля (для слепых); набор китайских иероглифов; набор знаков планет; набор знаков генетического кода.
Особенно важное значение имеют наборы, состоящие всего из двух знаков: пара знаков (+, -); пара знаков «точка», « тире»; пара цифр (0, 1); пара ответов (да, нет).
Наборы знаков, состоящие из 2 символов, называют двоичными - двоичный алфавит (0, 1), двоичный знак получил название БИТ. С появлением электрического телеграфа возникли важнейшие технические коды: азбука МОРЗЕ; набор знаков второго международного телеграфного кода (телекс).
Код используется для представления информации в виде, удобном для хранения и передачи.
Например, для того чтобы закодировать ряд чисел от 0 до 100, во-первых, нужно выбрать какой-то алфавит. Если для каждого числа придумать символ, который будет его обозначать, то потребуется 101 символ. А если чисел будет больше, то данный подход нерационален. Если каждое число представить (закодировать) не одним, а несколькими знаками из нашего алфавита, то в нашем правиле появится понятие длина кода.
Длиной кода – это такое количество знаков, которое используется при кодировании для представления символа. Количество символов в алфавите и длина кода – совершенно разные вещи. Например, в русском алфавите 33 буквы, а слова могут быть длиной в 1, 2, 3 и т.д. буквы.
Коды бывают постоянной и переменной длины. Коды переменной длины применяются в технике довольно редко. Исключением лишь является код МОРЗЕ. Азбука МОРЗЕ – это троичный код с набором знаков: точка, тире, пауза. Паузу необходимо использовать в качестве разделителя между буквами и словами, так как длина кода непостоянна. Если бы длина кода была постоянной, то расположение символов можно было устанавливать при помощи отсчета. В этом случае пауза не нужна. Сообщение будет раскодировано однозначно.
Применение кодов с постоянной длиной позволяет использовать для кодирования всего лишь два знака (двоичный код). Чем меньше букв в алфавите, тем должно быть проще устройство для раскодирования (расшифровки) информационного сообщения. Чем меньше букв в алфавите, тем больше должна быть длина кода.
В процессе развития человеческого общества люди выработали большое число языков кодирования: разговорные языки (русский, английский, хинди и др.); язык мимики и жестов; язык рисунков и чертежей; язык науки (математические, химические и другие символы); язык искусства (музыки, живописи, скульптуры и др.); специальные языки (эсперанто, морской семафор, азбука Морзе, азбука Брайля для слепых и др.); языки программирования (Бейсик, Паскаль, Фортран, Си и др.).
Программирование – это кодирование информации на языке, «понятном» компьютеру.
В компьютерах используется двоичная форма представления данных. Троичное кодирование, несмотря на ряд технических попыток, успеха не имело. Четверичное кодирование в криптографических целях (криптография – тайнопись) использовалось еще в XV веке. Передача сообщения всегда осуществляется во времени. Кодирование требует определенного количества времени, которым зачастую нельзя пренебрегать. При кодировании могут ставиться определенные цели и применяться различные методы.
Наиболее распространенные цели кодирования:
экономность (уменьшение избыточности сообщения, повышение скорости передачи или обработки информации);
надежность (защита от случайных искажений);
сохранность (защита от нежелательного доступа к информации);
удобство физической реализации (двойное кодирование информации в компьютере);
удобство восприятия (схемы, таблицы).
3.1. Кодирование информации в компьютере
В современных компьютерах используется двоичная форма представления данных, содержащая всего две цифры – 0 и 1. Такая форма позволяет создать достаточно простые технические устройства для представления (кодирования) и распознавания (дешифровки) информации. Двоичное кодирование выбрали потому, чтобы максимально упростить конструкцию декодирующей машины, ведь дешифратор должен уметь различать всего два состояния – 0 и 1. Например, 1 - есть ток в цепи, 0 – нет тока в цепи. По этой причине двоичная система и нашла такое широкое распространение.
Современный компьютер может обрабатывать числовую, текстовую, графическую, звуковую и видео информацию. Все эти виды информации в компьютере представлены в двоичном коде, т.е. используется алфавит мощностью два (всего два символа 0 и 1). Такое кодирование принято называть двоичным, а сами логические последовательности нулей и единиц - машинным языком.
| Вид информации | Двоичный код |
| Числовая | 10110011 |
| Текстовая | |
| Графическая | |
| Звуковая | |
| Видео |
Каждая цифра машинного двоичного кода несет количество информации равное одному биту. Данный вывод можно сделать, рассматривая цифры машинного алфавита, как равновероятные события. При записи двоичной цифры можно реализовать выбор только одного из двух возможных состояний, а, значит, она несет количество информации равное 1 бит. Следовательно, две цифры несут информацию 2 бита, четыре разряда - 4 бита и т.д. Чтобы определить количество информации в битах, достаточно определить количество цифр в двоичном машинном коде.
3.2. Кодирование текстовой информации
Большая часть пользователей при помощи компьютера обрабатывает текстовую информацию, которая состоит из символов: букв, цифр, знаков препинания и др.
Для того чтобы закодировать 1 символ используют количество информации равное 1 байту, т.е. I=1 байт = 8 бит. При помощи формулы ![]() , которая связывает между собой количество возможных событий N и количество информации I, можно вычислить, сколько различных символов можно закодировать:
, которая связывает между собой количество возможных событий N и количество информации I, можно вычислить, сколько различных символов можно закодировать: ![]() , т.е. для представления текстовой информации можно использовать алфавит мощностью 256 символов. Суть кодирования: каждому символу ставят в соответствие двоичный код от 00000000 до 11111111 или соответствующий ему десятичный код от 0 до 255.
, т.е. для представления текстовой информации можно использовать алфавит мощностью 256 символов. Суть кодирования: каждому символу ставят в соответствие двоичный код от 00000000 до 11111111 или соответствующий ему десятичный код от 0 до 255.
Для разных типов ЭВМ и операционных систем используются различные таблицы кодировки, отличающиеся порядком размещения символов алфавита в кодовой таблице. Международным стандартом на персональных компьютерах является уже упоминавшаяся таблица кодировки ASCII.
Принцип последовательного кодирования алфавита заключается в том, что в кодовой таблице ASCII латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Стандартными в этой таблице являются только первые 128 символов, т.е. символы с номерами от нуля (двоичный код 00000000) до 127 (01111111). Сюда входят буквы латинского алфавита, цифры, знаки препинания, скобки и некоторые другие символы. Остальные 128 кодов, начиная со 128 (двоичный код 10000000) и кончая 255 (11111111), используются для кодировки букв национальных алфавитов, символов псевдографики и научных символов.
В настоящее время для кодировки русских букв используют пять различных кодовых таблиц (КОИ-8, СР1251, СР866, Мас, ISO), причем тексты, закодированные при помощи одной таблицы, не будут правильно отображаться в другой кодировке.
В большинстве случаев о перекодировке текстовых документов заботится не пользователь, а специальные программы - конверторы, которые встроены в приложения.
Начиная с 1997 г. последние версии Microsoft Windows и Office поддерживают новую кодировку Unicode, которая на каждый символ отводит по 2 байта, а, поэтому, можно закодировать не 256 символов, а 65536 различных символов.
3.3. Кодирование графической информации
В видеопамяти находится двоичная информация об изображении, выводимом на экран. Почти все создаваемые, обрабатываемые или просматриваемые с помощью компьютера изображения можно разделить на две большие части - растровую и векторную графику.
Растровые изображения представляют собой однослойную сетку точек, называемых пикселами (pixel от англ. picture element), которые могут принимать только два значения: белый и черный (светится - не светится). Так как информация о цвете пиксела называется кодом пиксела, то для его кодирования достаточно одного бита памяти: 1 - белый, 0 - черный.
Если рассматривать иллюстрацию в виде комбинации точек с 256 градациями цвета, то достаточно восьмиразрядного двоичного числа, чтобы закодировать яркость любой точки. Цвет в компьютерной графике выступает средством усиления зрительного впечатления и повышения информационной насыщенности изображения. Восприятие цвета происходит в результате анализа светового потока, падающего на сетчатку глаза от отражающих или излучающих объектов. Цветовые рецепторы человека – колбочки и подразделяются на 3 группы, каждая из которых может воспринимать лишь один цвет (красный, зеленый или синий).
Пиксел на цветном дисплее может иметь различную окраску, поэтому одного бита на пиксел недостаточно. Для кодирования 4-цветного изображения требуются два бита на пиксел, поскольку два бита могут принимать 4 различных состояния. Может использоваться, например, такой вариант кодировки цветов: 00 - черный, 10 - зеленый, 01 - красный, 11 - коричневый.
На RGB-мониторах все разнообразие цветов получается сочетанием базовых цветов - красного (Red), зеленого (Green), синего (Blue), из которых можно получить 8 основных комбинаций.
Разумеется, если иметь возможность управлять интенсивностью (яркостью) свечения базовых цветов, то количество различных вариантов их сочетаний, порождающих разнообразные оттенки, увеличивается. Количество различных цветов - К и количество битов для их кодировки - N связаны между собой простой формулой: ![]() .
.
В противоположность растровой графике векторное изображение многослойно. Каждый элемент векторного изображения - линия, прямоугольник, окружность или фрагмент текста - располагается в своем собственном слое, пикселы которого устанавливаются независимо от других слоев. Каждый элемент векторного изображения является объектом, который описывается с помощью специального языка (математических уравнения линий, дуг, окружностей и т.д.). Сложные объекты (ломаные линии, различные геометрические фигуры) представляются в виде совокупности элементарных графических объектов.
Объекты векторного изображения, в отличии от растровой графики, могут изменять свои размеры без потери качества (при увеличении растрового изображения увеличивается зернистость).
3.4. Кодирование звука
Из курса физики вам известно, что звук - это колебания воздуха. Если преобразовать звук в электрический сигнал (например, с помощью микрофона), мы увидим плавно изменяющееся с течением времени напряжение. Для компьютерной обработки такой – аналоговый - сигнал нужно каким-то образом преобразовать в последовательность двоичных чисел.
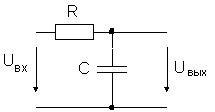
Будем измерять напряжение через равные промежутки времени и записывать полученные значения в память компьютера. Этот процесс называется дискретизацией (или оцифровкой), а устройство, выполняющее его - аналого-цифровым преобразователем (АЦП).
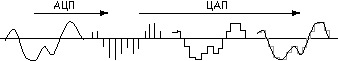
Для того чтобы воспроизвести закодированный таким образом звук, нужно выполнить обратное преобразование (для него служит цифро-аналоговый преобразователь - ЦАП), а затем сгладить получившийся ступенчатый сигнал.
Чем выше частота дискретизации (т.е. количество отсчетов за секунду) и чем больше разрядов отводится для каждого отсчета, тем точнее будет представлен звук. При этом увеличивается и размер звукового файла. В зависимости от характера звука, требований, предъявляемых к его качеству и объему занимаемой памяти, выбирают некоторые компромиссные значения.
Описанный способ кодирования звуковой информации достаточно универсален, он позволяет представить любой звук и преобразовывать его самыми разными способами. Но бывают случаи, когда выгодней действовать по-иному.
Человек издавна использует довольно компактный способ представления музыки - нотную запись. В ней специальными символами указывается, какой высоты звук, на каком инструменте и как сыграть. Фактически, ее можно считать алгоритмом для музыканта, записанным на особом формальном языке. В 1983 г. ведущие производители компьютеров и музыкальных синтезаторов разработали стандарт, определивший такую систему кодов. Он получил название MIDI. Такая система кодирования позволяет записать далеко не всякий звук, годится только для инструментальной музыки. Есть неоспоримые преимущества: чрезвычайно компактная запись, естественность для музыканта, легкость замены инструментов, изменения темпа и тональности мелодии [3].
Существуют и другие, чисто компьютерные, форматы записи музыки, например, формат MP3, позволяющий с очень большим качеством и степенью сжатия кодировать музыку.
3.5. Кодирование чисел
Существуют два основных формата представления чисел в памяти компьютера. Один из них используется для кодирования целых чисел, второй (так называемое представление числа в формате с плавающей точкой) используется для задания некоторого подмножества действительных чисел.
Множество целых чисел, представимых в памяти ЭВМ, ограничено. Диапазон значений зависит от размера области памяти, используемой для размещения чисел. В k-разрядной ячейке может храниться 2k различных значений целых чисел.
Чтобы получить внутреннее представление целого положительного числа N, хранящегося в k-разрядном машинном слове, необходимо:
1) перевести число N в двоичную систему счисления;
2) полученный результат дополнить слева незначащими нулями до k разрядов.
Формат с плавающей точкой использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления n в некоторой целой степени p, которую называют порядком: ![]() . Представление числа в форме с плавающей точкой неоднозначно. Например, справедливы следующие равенства:
. Представление числа в форме с плавающей точкой неоднозначно. Например, справедливы следующие равенства:
12.345 = 0.0012345 x 104 = 1234.5. x 10-2 = 0.12345 x 102
Чаще всего в ЭВМ используют нормализованное представление числа в форме с плавающей точкой. Мантисса в таком представлении должна удовлетворять условию: ![]() . Иначе говоря, мантисса меньше 1 и первая значащая цифра - не ноль (p - основание системы счисления).
. Иначе говоря, мантисса меньше 1 и первая значащая цифра - не ноль (p - основание системы счисления).
В памяти компьютера мантисса представляется как целое число, содержащее только значащие цифры (0 целых и запятая не хранятся), так для числа 12.345 в ячейке памяти, отведенной для хранения мантиссы, будет сохранено число 12345. Для однозначного восстановления исходного числа остается сохранить только его порядок, в данном примере - это 2.
3.6. Понятие о системах счисления3.6.1. Что такое система счисления
Системой счисления называется совокупность приемов наименования и записи чисел [7].
Система счисления - это способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.
В любой системе счисления для представления чисел выбираются некоторые символы (слова или знаки), называемые базисными числами, а все остальные числа получаются в результате каких-либо операций из базисных чисел данной системы исчисления. Символы, используемые для записи чисел, могут быть любыми, только они должны быть разными и значение каждого из них должно быть известно.
В современном мире наиболее распространенным является представление чисел посредством арабских цифр 0, 1,2, 3, 4, 5, 6, 7, 8, 9 - специальных знаков, используемых для записи чисел. Системы счисления различаются выбором базисных чисел и правилами образования из них остальных чисел.
Системы счисления, в которых любое число получается путем сложения или вычитания базисных чисел, называются аддитивными. При таком представлении чисел правила сложения для небольших чисел очевидны и просты, однако если возникает необходимость выполнять операции сложения над большими числами или операции умножения и деления, то «римская» система счисления оказывается неудобной.
В этой ситуации преимущественнее оказываются позиционные системы счисления.
Существуют позиционные и непозиционные системы счисления.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. В позиционной системе счисления представления чисел далеко не так просты и очевидны, как в «римской» системе счисления, систематичность представления, основанная на «позиционном весе» цифр, обеспечивает простоту выполнения операций умножения и деления.
В непозиционных системах вес цифры (т.е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. В «римской» системе счисления каждый числовой знак в записи любого числа имеет одно и то же значение, т.е. значение числового знака не зависит от его расположения в записи числа. В римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти, а I – это единица.
Для изображения чисел в настоящее время используются в основном позиционные системы счисления. Привычной для всех является десятичная система счисления. В этой системе для записи любых чисел используется только десять разных знаков (цифр): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Эти цифры введены для обозначения первых десяти последовательных чисел, а следующее число 10 и т.д. обозначается уже без использования новых цифр. Однако введением этого обозначения сделан важный шаг в построении системы счисления: значение каждой цифры поставлено в зависимость от того места, где она стоит в изображении числа.
Десятичная запись любого числа X в виде последовательности цифр: ![]() , основана на представлении этого числа в виде полинома:
, основана на представлении этого числа в виде полинома:
![]() ,
,
где каждый коэффициент аi, может быть одним из чисел, для обозначения которых введены специальные знаки. Запись числа X в формуле представляет собой просто перечисление всех коэффициентов этого полинома. Точка, отделяющая целую часть числа от дробной, служит для фиксации конкретных значений каждой позиции в этой последовательности цифр и является началом отсчета.
Количество К различных цифр, употребляющихся в позиционной системе счисления, называется ее основанием системы счисления, а сама система счисления называется К-ичной. Например, основанием десятичной системы счисления является число 10; двоичной - число 2; троичной - число 3 и т.д. Для записи произвольного числа в K-ичной системе счисления достаточно иметь К разных цифр ![]() . Эти цифры служат для обозначения некоторых различных целых чисел, называемых базисными.
. Эти цифры служат для обозначения некоторых различных целых чисел, называемых базисными.
Запись произвольного числа X в K-ичной позиционной системе счисления основывается на представлении этого числа в виде полинома:
![]() ,
,
где каждый коэффициент а, может быть одним из базисных чисел и изображается одной цифрой. В качестве базисных чисел берутся последовательные целые числа от 0 до К-1 включительно.
Позиции цифры, отсчитанные от запятой (точки), отделяющей целую часть от дробной, называются разрядами. В позиционной системе счисления вес каждого разряда больше соседнего в число раз, равное основанию системы К.
Пример: Для десятичной системы счисления (основание К=10) имеем число 6321.564. Веса разряда и коэффициенты а для этого числа будут следующими:
![]()
Все известные позиционные системы счисления являются аддитивно-мультипликативными. Особенно отчетливо аддитивно-мультипликативный способ образования чисел из базисных выражен в числительных русского языка, например пятьсот шестьдесят восемь (т.е.5 сотен + 6 десятков + 8).
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими полиномами. Нужно только пользоваться теми таблицами сложения и умножения, которые имеют место при данном основании К системы счисления. Во всех позиционных системах счисления с любым основанием К умножения на числа вида Кm, где m - целое число, сводится просто к перенесению запятой у множимого на m разрядов вправо или влево (в зависимости от знака m), так же как и в десятичной системе.
Для указания того, в какой системе счисления записано число, условимся при его изображении основание системы счисления указывать в виде нижнего индекса при нем, например, 35,648 или подстрочным индексом, заключенным в круглые скобки, например: 1101(2).
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
Продвижением цифры называют замену её следующей по величине. Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д. Продвижение старшей цифры (например, цифры 9 в десятичной системе) означает замену её на 0. В двоичной системе, использующей только две цифры – 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 – замену её на 0.
Целые числа в любой системе счисления порождаются с помощью Правила счета:
Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
В настоящее время в ЭВМ применяют двоичную, восьмеричную и шестнадцатеричную системы счисления.
3.6.2. Двоичная система счисления
В современной вычислительной технике, в устройствах автоматики, связи используется двоичная система счисления - система счисления с наименьшим возможным основанием, где для изображения числа используются две цифры: 0 и 1.
Двоичная система счисления имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток - нет тока, намагничен - не намагничен и т.п.);
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.
Недостаток двоичной системы - быстрый рост числа разрядов, необходимых для записи чисел, т.е. в громоздкости записи чисел, но это не имеет существенного значения для ЭВМ. Если возникает необходимость кодировать информацию «вручную», например, при составлении программы на машинном языке, предпочтительнее оказывается пользоваться восьмеричной, или шестнадцатеричной системой счисления.
Произвольное число X в двоичной системе представляется в виде полинома:
![]() ,
,
где каждый коэффициент аi может быть либо 0, либо 1.
Пример: Двоичное число - 1011012
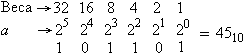 ,
,
т.е. ![]() .
.
Для отделения целой части от дробной используется точка (запятая). Значение веса разрядов справа от точки (запятой) равно основанию двоичной системы (2), возведенному в отрицательную степень. Такие веса - это дроби вида: 1/2, 1/22, 1/23, 1/24, 1/25 или 1/2, 1/4, 1/8, 1/16.
Каждая позиция, занятая двоичной цифрой, называется бит. Бит является наименьшей единицей информации в ЭВМ. Наименьшим значащим битом (МЗР) называют самый младший двоичный разряд, а самым старшим двоичным разрядом - наибольший значащий бит (СЗР). В двоичном числе эти биты имеют, соответственно, наименьший и наибольший вес. Обычно двоичное число записывают так, что старший значащий бит является крайним слева.
3.6.3. Восьмеричная система счисления
В восьмеричной системе счисления базисными числами являются 0, 1, 2, 3, 4, 5, 6, 7. Запись любого числа в этой системе основывается на его разложении по степеням числа восемь с коэффициентами, являющимися указанными выше базисными числами.
Произвольное число X в восьмеричной системе представляется в виде полинома:
![]() ,
,
где каждый коэффициент аi может быть 0, 1, 2, 3, 4, 5, 6, 7.
Например, десятичное число 83,5 в восьмеричной системе будет изображаться в виде 123,48 и в виде полинома:
![]()
Восьмеричная система счисления не нужна ЭВМ в отличие от двоичной системы. Она удобна как компактная форма записи чисел и используется программистами (например, в текстах программ для более краткой и удобной записи двоичных кодов команд, адресов и операндов).
В восьмеричной системе счисления вес каждого разряда кратен восьми (1/8), поэтому восьмиразрядное двоичное число позволяет выразить десятичные величины в пределах 0-255, а восьмеричное охватывает диапазон 0 - 99999999.Т. к.8=23, то каждый восьмеричный символ можно представить трехбитовым двоичным числом.
Для перевода числа из двоичной системы счисления в восьмеричную необходимо разбить это число влево (для целой части) и вправо (для дробной) от точки (запятой) на группы по три разряда (триады) и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняются необходимым количеством незначащих нулей.
Перевод из восьмеричной системы счисления в двоичную систему осуществляется путем представления каждой цифры восьмеричного числа трехразрядным двоичным числом.
3.6.4. Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления базисными являются числа от нуля до пятнадцати. Эта система отличается от рассмотренных ранее тем, что в ней общепринятых (арабских) цифр не хватает для обозначения всех базисных чисел, поэтому приходится вводить в употребление новые символы. Обычно для обозначения первых десяти целых чисел от нуля до девяти используют арабские цифры, а для следующих целых чисел от десяти до пятнадцати используются буквенные обозначения A, B, C, D, E, F.
Произвольное число X в восьмеричной системе представляется в виде полинома:
![]() ,
,
где каждый коэффициент аi может быть 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F: ![]()
Шестнадцатеричная система счисления позволяет еще короче записывать многоразрядные двоичные числа и, кроме того, сокращать запись 4-разрядного двоичного числа, т.е. полубайта, поскольку 16=24. Шестнадцатеричная система так же применяется в текстах программ для более краткой и удобной записи двоичных чисел.
Для перевода числа из двоичной системы счисления в шестнадцатеричную, необходимо разбить это число влево и вправо от точки на тетрады и представить каждую тетраду цифрой в шестнадцатеричной системе счисления.
Для перевода числа из шестнадцатеричной системы счисления в двоичную, необходимо наоборот каждую цифру этого числа заменить тетрадой.
3.6.5. Переводы чисел, простейшая арифметика в системах счисления
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.
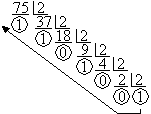
Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
| 2-я с. с. | 8-я с. с. | 16-я с. с. |
|
|
|
|
Ответ: 7510 = 1 001 0112 = 1138 = 4B16
При переводе числа из двоичной (8-чной, 16-ричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.
Пример:
Разряды 3 2 1 0 - 1
Число 1011,12=1*23+1*21+1*20+1*2-1=11,510.
Разряды 2 1 0 - 1
Число 276,58=2*82+7*81+6*80+5*8-1=190,62510.
Разряды 2 1 0
Число 1F316=1*162+15*161+3*160=49910.
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой или тетрадой.
Пример:
![]() ;
; ![]()
Чтобы перевести число из двоичной системы в восьмеричную (шестнадцатеричную), его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной), каждую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Пример:
![]()
![]()
При переводе правильной десятичной дроби в систему счисления с основанием q нужно саму дробь, затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения. Умножение производится до тех пор, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности.
Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Двоичная с. с. | Восьмеричная с. с. | Шестнадцатеричная с. с. |
|
|
|
|
Ответ: 0,3510 = 0,010112 = 0,2638 = 0,5916.
Арифметические операции в позиционных системах счисления.
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны - это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления, но нужно пользоваться соответствующими таблицами сложения и умножения.
Сложение
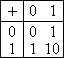
Таблицы сложения составляются с помощью Правила Счета:
| 2-я с. с. | 8-я с. с. | 16-я с. с. |
|
|
|
|
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
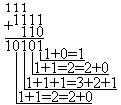
Пример: Сложим числа 15 и 6 в 2, 8, 16 системах счисления.
| 2-я с. с. | 8-я с. с. | 16-я с. с. |
|
|
|
|
Ответ: 15+6 = 2110 = 101012 = 258 = 1516.
Вычитание
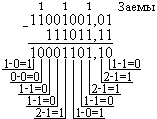
Пример: Вычтем число 59,75 из числа 201,25.
| 2-я с. с. | 8-я с. с. | 16-я с. с. |
|
|
|
|
Ответ: 201,2510–59,7510=141,510=10001101,12=215,48=8D,816.
Умножение
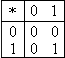
| Двоичная система | Восьмеричная система |
|
|
|
Пример: Перемножим числа 5 и 6.
| 10-я с. с. | 2-я с. с. | 8-я с. с. |
|
|
|
|
Ответ: 5*6 = 3010 = 111102 = 368.
Деление
Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе.
Пример. Разделим число 30 на число 6.
| 10-я с. с. | 2-я с. с. | 8-я с. с. |
|
|
|
|
Ответ: 30: 6 = 510 = 1012 = 58.
3.6.6. Как представляются в компьютере целые числаЦелые числа могут представляться в компьютере со знаком или без знака. Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 000000002 до 111111112, а в двубайтовом формате - от 00000000 000000002 до 11111111 111111112.
Диапазоны значений целых чисел без знака
| Формат числа в байтах | Диапазон | |
| Запись с порядком | Обычная запись | |
| 1 | 0...28–1 | 0...255 |
| 2 | 0...216–1 | 0...65535 |
Примеры:
а) число 7210 = 10010002 в однобайтовом формате:
![]()
б) это же число в двухбайтовом формате:
![]()
в) число 65535 в двухбайтовом формате:
![]()
Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак “плюс” кодируется нулем, а “минус” - единицей.
Диапазоны значений целых чисел со знаком
| Формат числа в байтах | Диапазон | |
| Запись с порядком | Обычная запись | |
| 1 | –27...27–1 | –128...127 |
| 2 | –215...215–1 | –32768...32767 |
| 4 | –231...231–1 | –2147483648...2147483647 |
Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины – семь разрядов.
В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код (ПК), обратный код (ОК), дополнительный код (ДК).
Общая идея построения кодов такова. Код трактуется как число без знака, а диапазон представляемых кодами чисел без знака разбивается на два поддиапазона. Один из них представляет положительные числа, другой - отрицательные. Разбиение выполняется таким образом, чтобы принадлежность к поддиапазону определялась максимально просто.
Наиболее распространенным и удобным является формирование кодов таким образом, чтобы значение старшего разряда указывало на знак представляемых чисел, т.е. использование такого кодирования позволяет говорить о старшем разряде как о знаковом (бит знака) и об остальных как о цифровых разрядах кода.
Обратный и дополнительный коды применяются широко, так как позволяют упростить конструкцию арифметико-логического устройства (АЛУ) компьютера путем замены разнообразных арифметических операций операцией сложения.
Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково - двоичными кодами с цифрой 0 в знаковом разряде.
| Например: | Число 110=12 | Число 12710=11111112 |
|
|
|
Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
Похожие работы
... техникой всех отраслей человеческой деятельности остро ставит вопрос о технологическом обеспечении информационных систем и технологий. Технологическое обеспечение реализует информационные процессы в автоматизированных системах организационного управления с помощью ЭВМ и других технических средств. Разработка технологического обеспечения требует учета особенностей структуры экономических систем. ...
... корпоративных систем. Развитие последних произошло за счет международной и национальной стандартизации аппаратных и программных интерфейсов. Главной причиной развития концепции открытых систем в маркетинговой деятельности явился повсеместный переход к использованию локальных вычислительных сетей и те проблемы комплексирования аппаратно-программных средств, которые вызвал этот переход, В связи с ...
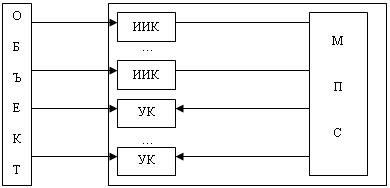
... при механических, климатических и специальных воздействиях окружающей среды; - специальные требования по защите информации. Построение «автоматизированной системы информационной поддержки наладочных работ электропривода» Дано: 1 Объект информатизации 2 Ограничения 3 Критерий 4 База данных 5 Классификатор характеристик 6 Пакет программ ...
... БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Моделирование и обработка данных, поступающих от аналого-цифровых преобразователей: Методические указания к выполнению лабораторной работы по дисциплине "Обработка данных в автоматизированных системах" / Сост. Л.А. Краснодубец. – Севастополь: Изд-во СевНТУ, 2002.–11с. 2. Исследование дискретного преобразования Фурье: Методические указания к выполнению лабораторной ...



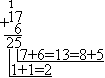





0 комментариев