Навигация
Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа - двоичный код его абсолютной величины
1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа - двоичный код его абсолютной величины.
| Например: | Прямой код числа - 1 | Прямой код числа - 127 |
|
|
|
Сложение в прямом коде чисел, имеющих одинаковые знаки: числа складываются, и сумме присваивается знак слагаемых. Более сложным является алгебраическое сложение в прямом коде чисел с разными знаками. В этом случае приходится определять большее по модулю число, производить вычитание модулей и присваивать разности знак большего по модулю числа. Такую операцию проще выполнять, используя обратный и дополнительный коды.
2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, единицы - нулями.
Например:
| Число - 1 Код модуля числа: 0 0000001 Обратный код числа: 1 1111110
| Число - 127 Код модуля числа: 0 1111111 Обратный код числа: 1 0000000
|
В общем случае ОК является дополнением модуля исходного числа до наибольшего числа без знака, помещенного в разрядную сетку. Алгоритм формирования ОК очень прост, при этом ОК позволяет унифицировать операции сложения и вычитания в АЛУ, которые в прямом коде выполняются по-разному. Однако работа с ОК вызывает ряд трудностей. В частности, возникают два нуля: +0 и - 0, т.е. в прямом коде (в котором представлены положительные числа) имеет место (+0) = 000...0, а в обратном коде (в котором представлены отрицательные числа): (-0) = 111...1.
Кроме того, в операциях сложения и вычитания требуется дополнительная операция по прибавлению бита переноса в младший разряд суммы. Рассмотрим правила алгебраического сложения в ОК (поскольку А-В=А+(-В)). Алгоритм сложения в ОК включает в себя:
сложение кодов, включая знаковый разряд;
прибавление переноса к младшему значащему разряду (МЗР) суммы.
Пример: Вычислить выражение: - 310 - 210.

Бит знака в ОК равен 1, следовательно, получаем отрицательное число: - 510.
Пример: Вычислить 710 - 310.

Бит знака равен нулю, следовательно, получаем положительное число в ПК: 410.
Указанные трудности привели к тому, что в современных ЭВМ абсолютное большинство операций выполняется в дополнительном коде.
3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
Например:
| Дополнительный код числа - 1 | Дополнительный код числа - 127 |
|
|
|
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
Сложение и вычитание в дополнительном коде
При выполнении арифметических операций в современных ЭВМ используется представление положительных чисел в прямом коде, а отрицательных - в обратном или в дополнительном кодах. Это можно проиллюстрировать схемой на следующем рисунке:

На рисунке а) представление положительных чисел, б) – отрицательных.
Общее правило. При алгебраическом сложении двух двоичных чисел, представленных обратным (или дополнительным) кодом, производится арифметическое суммирование этих кодов, включая разряды знаков. При возникновении переноса из разряда знака единица переноса прибавляется к МЗР суммы кодов при использовании ОК и отбрасывается при использовании ДК. В результате получается алгебраическая сумма в обратном (или дополнительном) коде.
Рассмотрим подробнее алгебраическое сложение для случая представления отрицательных чисел в ДК.
При алгебраическом сложении чисел со знаком, результатом также является число со знаком. Суммирование происходит по всем разрядам, включая знаковые, которые при этом рассматриваются как старшие. При возникновении переноса из старшего разряда единица переноса отбрасывается и возможны два варианта результата:
знаковый разряд равен нулю: результат - положительное число в ПК;
знаковый разряд равен единице: результат - отрицательное число в ДК.
Для определения абсолютного значения результата, его необходимо инвертировать, затем прибавить единицу.
Пример: Вычислить алгебраическую сумму 58 - 23.

Перенос из знакового разряда отбрасываем. Число является положительным в ПК: 3510.
Признак переполнения разрядной сетки
При алгебраическом суммировании двух чисел, помещающихся в разрядную сетку, может возникнуть переполнение, то есть образуется сумма, требующая для своего представления на один двоичный разряд больше, чем разрядная сетка слагаемых. Предполагается, что положительные числа представляются в прямом коде, а отрицательные - в дополнительном.
Признаком переполнения является наличие переноса в знаковый разряд суммы при отсутствии переноса из знакового разряда (положительное переполнение) или наличие переноса из знакового разряда суммы при отсутствии переноса в знаковый разряд (отрицательное переполнение).
При положительном переполнении результат операции положительный, а при отрицательном переполнении - отрицательный. Если и в знаковый, и из знакового разряда суммы есть переносы или этих переносов нет, то переполнение отсутствует.
Похожие работы
... техникой всех отраслей человеческой деятельности остро ставит вопрос о технологическом обеспечении информационных систем и технологий. Технологическое обеспечение реализует информационные процессы в автоматизированных системах организационного управления с помощью ЭВМ и других технических средств. Разработка технологического обеспечения требует учета особенностей структуры экономических систем. ...
... корпоративных систем. Развитие последних произошло за счет международной и национальной стандартизации аппаратных и программных интерфейсов. Главной причиной развития концепции открытых систем в маркетинговой деятельности явился повсеместный переход к использованию локальных вычислительных сетей и те проблемы комплексирования аппаратно-программных средств, которые вызвал этот переход, В связи с ...
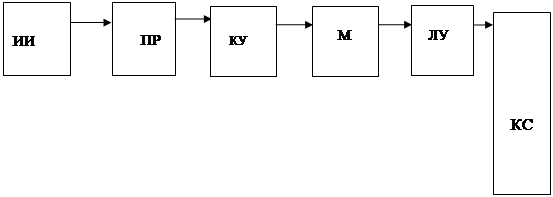
... при механических, климатических и специальных воздействиях окружающей среды; - специальные требования по защите информации. Построение «автоматизированной системы информационной поддержки наладочных работ электропривода» Дано: 1 Объект информатизации 2 Ограничения 3 Критерий 4 База данных 5 Классификатор характеристик 6 Пакет программ ...
... БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Моделирование и обработка данных, поступающих от аналого-цифровых преобразователей: Методические указания к выполнению лабораторной работы по дисциплине "Обработка данных в автоматизированных системах" / Сост. Л.А. Краснодубец. – Севастополь: Изд-во СевНТУ, 2002.–11с. 2. Исследование дискретного преобразования Фурье: Методические указания к выполнению лабораторной ...

0 комментариев