Министерство образования и науки Украины
Севастопольский национальный технический университет
Кафедра Радиотехники
Расчетно-графическое задание №1по дисциплине “Радиоавтоматика”
Исследование частотно-временных характеристик и структурных преобразований систем радиоавтоматики
Выполнила: ст. гр. Р-41д
Грибенщиков А.А.
Проверил: профессор
Бабуров Э.Д.
Севастополь 2008Задание №1
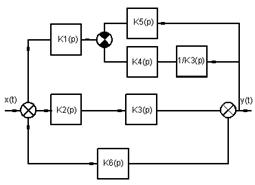
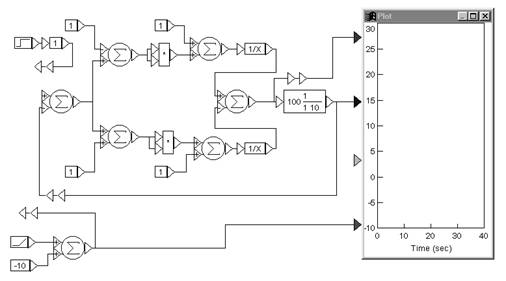
1.1 Для системы радиоавтоматики, схема которой приведена на рисунке 1, определить передаточные функции системы по управляющему сигналу и по помехе.
1.2 Для системы радиоавтоматики, схема которой приведена на рисунке 4, записать дифференциальное уравнение системы, определить аналитически и построить графически переходную и импульсную характеристики.
1.3 Построить амплитудно-фазовую характеристику разомкнутой системы.
1.4 Построить логарифмические амплитудно-частотную и фазо-частотную характеристики разомкнутой системы.
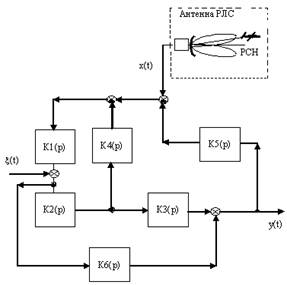
Рис. 1 – Структурная схема системы 1.
x(t) - входное управляющее воздействие;
y(t) - выходной регулируемый сигнал;
x(t)- помеха;
Кi(р) - передаточные функции звеньев системы
1.1 Для системы радиоавтоматики, схема которой приведена на рисунке 1, определим передаточные функции системы по управляющему сигналу и по помехе. Как известно, коэффициент передачи цепи, охваченной обратной связью, определяется по формуле
![]() (1)
(1)
где Кос(р) - коэффициент передачи обратной связи.
Передаточные функции звеньев системы 1 для данного варианта приведены в таблице 1.
Таблица 1 – Исходные данные
| № варианта | К1(р) | К2(р) | К3(р) | К4(р) | К5(р) | К6(р) |
| 8 | р-2 | р+1 | (р+58)-1 | 17р+10 | р | р-2 |
Для удобства вычисления передаточной функции системы по управляющему сигналу упростим структурную схему системы 1 и изобразим её на рисунке 2. Упрощение произведём следующим образом: выходы звеньев 4 и 5 соединим и заведём на обратную (отрицательную) связь в одну точку. Также перенесём вход звена 4 с точки соединения звеньев 2 и 3 на выход звена 3 при этом переносе добавим последовательно перед входом звена 4 звено с передаточной функцией обратной К3(р).
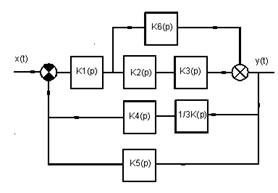 |
Рис. 2 – Упрощённая структурная схема системы 1(по управляющему сигналу)
Определим передаточную функцию системы 1 по управляющему сигналу.
![]() ,
, ![]()
![]()
К4![]() (р)=
(р)= ![]() К4
К4![]() 5(р)= К5(р)+
5(р)= К5(р)+![]()
Тогда передаточная функция системы 1 К(р) будет равна:
К(р)=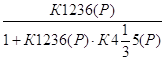
Подставив значения К1236(р) и К4![]() 5(р) получим:
5(р) получим:
К(р)=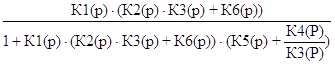
Подставим значения передаточных функций звеньев из таблицы 1, получим:
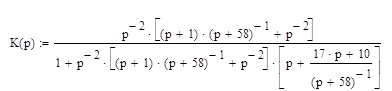
После упрощений, с использованием математического пакета MathCAD 2001 имеем:
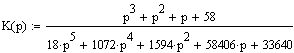
 |
Определим передаточную функцию системы 1 по помехе, упрощенная структурная схема которой изображена на рисунке 3.
Рис. 3 – Упрощенная структурная схема
Очевидны следующие формулы:
![]()
![]()
![]()
![]()
Тогда с учетом (1) можно записать
![]()
Подставим значения передаточных функций звеньев из таблицы 1, тогда получим:
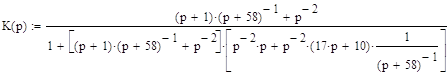
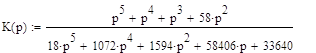
Для системы радиоавтоматики, схема которой приведена на рисунке 4 запишем дифференциальное уравнение системы, определим аналитически и построим графически переходную и импульсную характеристики.
Коэффициент передачи определяется по формуле
![]()
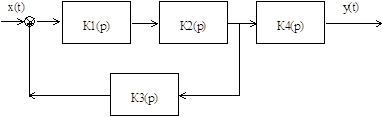
Подставим значения передаточных функций звеньев из таблицы 1, тогда получим:
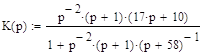
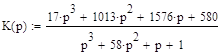
Напишем уравнение системы, на основании передаточной функции
![]()
где в скобках есть номер производной.
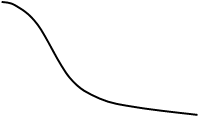
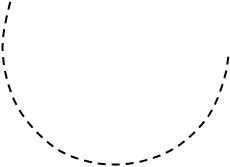
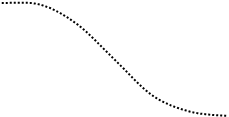
Определим переходную характеристику системы.
Переходная характеристика h(t) есть реакция динамического элемента на воздействие на воздействие в виде единичной ступенчатой функции 1(t):
![]()
![]()
где ![]() символ обратного преобразования Лапласа.
символ обратного преобразования Лапласа.
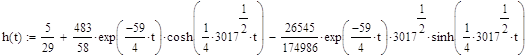
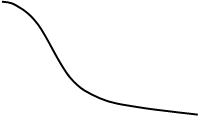
Определим импульсную характеристику системы:
Импульсная характеристика – это реакция динамического элемента на воздействие в виде d-функции:
![]()
Импульсная характеристика может быть определена как обратное преобразование Лапласа от передаточной функции динамического элемента:
![]()
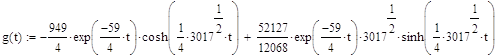
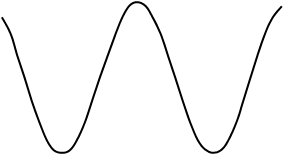
Построим переходную и импульсную характеристики:
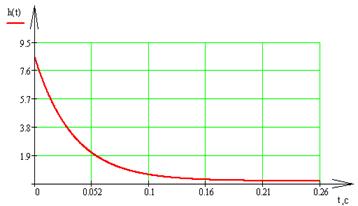
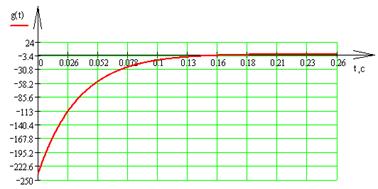
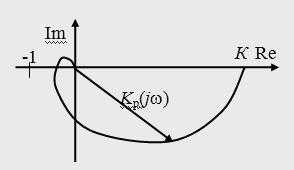
3) Построить амплитудно-фазовую характеристику разомкнутой системы, схема которой приведена на рисунке 4.
Для перехода к разомкнутой системе преобразуем схему следующим образом:
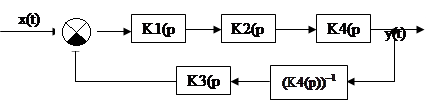
Разомкнув цепь обратной связи, получим:
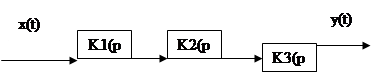
Рис. 7 – Структурная схема разомкнутой системы
Определим передаточную функцию разомкнутой системы:
![]()
![]()
Заменим p на jw:
![]()
![]()
![]()
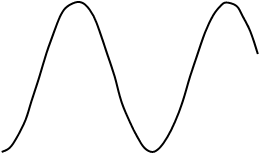
Построим график амплитудно-фазовой характеристики:
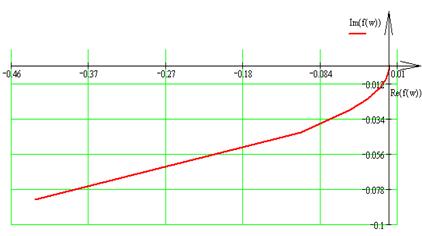
|
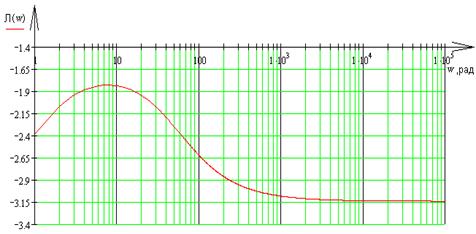
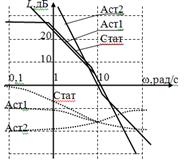
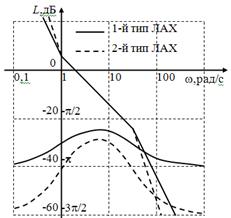
4) Построить логарифмические амплитудно-частотную и фазо-частотную характеристики разомкнутой системы, схема которой приведена на рисунке 4
Логарифмическая амплитудно-частотная характеристика определяется формулой:
![]()
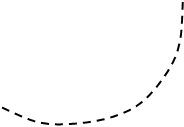
Построим ЛАХ и ЛФХ:
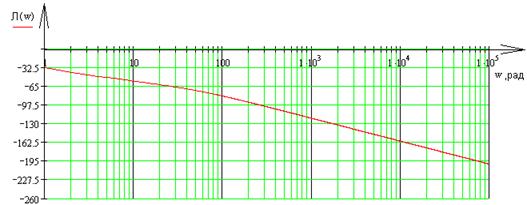
Похожие работы
... характеристик системы в установившемся режиме составляется статическая модель. В ней отражаются только функциональные преобразования процессов. Статическая модель системы изображена на рис. 4. При ее составлении учитывалось, что для постоянного воздействия коэффициент передачи ФНЧ равен 1, а частота перестраиваемого генератора fп г = fпг0 + Dfпг, где fпг0 – частота ПГ при управляющем ...
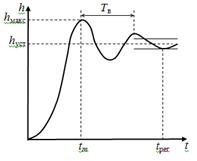
... частот, то переходная характеристика будет колебательной. Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4). Рис. Обычно используются следующие числовые параметры переходной характеристики: время достижения ...
... , которая компенсируется системой ФАПЧ. По этой модели составляется дифференциальное уравнение в операторной форме: . Учитывая, что р – оператор дифференцирования и рjн = 0, получаем: связь фаза автоподстройка . (1) Система ФАПЧ в установившемся режиме поддерживает разность фаз входных колебаний постоянной. Следовательно, в установившемся режиме dj/dt = 0 и, как ...
... Рис. 6 Рис. 7 Схема моделирования показана на рис. 8. Рис.8 Исследование устойчивости для удобства сравнения проводится на трех моделях, отличающихся структурой или параметрами. 2.Оптимальные линейные САР Задача оптимального синтеза линейной системы авторегулирования при случайных воздействиях заключается в определении такой структуры и параметров системы, при ...


0 комментариев