Навигация
Частотные и переходные характеристики систем авторегулирования
Введение
Радиопередающие устройства (РПдУ) применяются в сферах телекоммуникации, телевизионного и радиовещания, радиолокации, радионавигации. Стремительное развитие микроэлектроники, аналоговой и цифровой микросхемотехники, микропроцессорной и компьютерной техники оказывает существенное влияние на развитие радиопередающей техники как с точки зрения резкого увеличения функциональных возможностей, так и с точки зрения улучшения ее эксплуатационных показателей. Это достигается за счет использования новых принципов построения структурных схем передатчиков и схемотехнической реализации отдельных их узлов, реализующих цифровые способы формирования, обработки и преобразования колебаний и сигналов, имеющих различные частоты и уровни мощности.
1. Частотные и переходные характеристики систем авторегулирования
Частотная и переходная характеристики замкнутой системы являются показателями качества при гармоническом и скачкообразном воздействиях. Если задающее воздействие гармоническое:
xз(t) = Acoswt,
то выходной процесс линейной системы тоже гармонический:
y(t) = AKз(w)cos(wt + jз(w)),
где Кз(w) и jз(w), соответственно, - АЧХ и ФЧХ замкнутой системы.
d(t) = xз(t) – y(t) = Acoswt – AKз(w)cos(wt + jз(w))
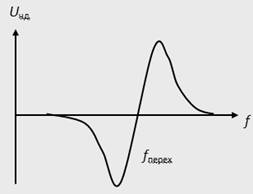
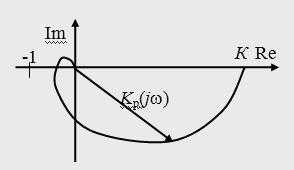
будет равна нулю только при Кз(w) = 1 и jз(w) = 0. Это требование к идеальной частотной характеристике замкнутой системы. Если все составляющие спектра задающего воздействия попадают в область частот, где частотная характеристика идеальна, то воздействие отрабатывается без ошибки. В противном случае возникает динамическая ошибка.Для оценки качества регулирования по АЧХ замкнутой системы используется показатель колебательности М = Кмакс/Кз(0) (см. рис. 1). Обычно величина показателя колебательности меньше 2.
![]()
Рис.1
![]()
Так как АЧХ будет близка к 1, если Кр(w)>>1, независимо от вида частотной характеристики разомкнутой системы в этой области частот.
Для примера рассмотрим системы авторегулирования разного типа: статическую и астатические первого и второго порядка, передаточные функции которых описываются выражениями:
![]() ,
,
![]() ,
, ![]() .(1)
.(1)
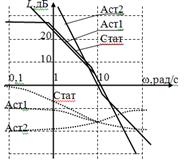
Рис.
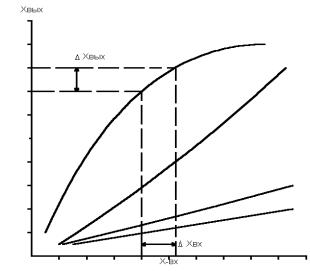
Их логарифмические амплитудные характеристики, как видно из рис. 2, значительно отличаются в области нижних и верхних частот. Однако если запасы устойчивости в этих системах одинаковы, то различие в амплитудно-частотных характеристиках замкнутых систем невелико (см. рис. 3). Запас устойчивости по фазе для каждой из этих систем определяется выражениями:
Δφ1 = 180 – arctg10ωсрT1 – arctgωсрТ1,
Δφ2 = 90 – arctgωсрT2, (2)
Δφ3 = arctgωсрТ3.
По форме АЧХ можно судить о переходной характеристике системы. Так, если АЧХ будет монотонной, то и переходная характеристика монотонна, если в АЧХ будет подъем в области верхних частот, то переходная характеристика будет колебательной.
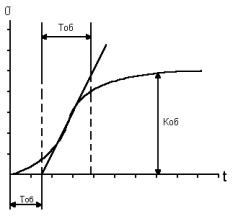
Переходная характеристика является показателем качества при быстро изменяющемся воздействии. Для систем авторегулирования лучшей считается колебательная переходная характеристика с быстрым затуханием колебаний на вершине (рис. 4).
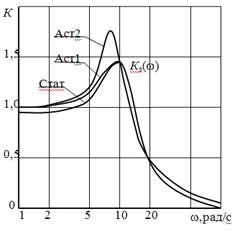
Рис.
Обычно используются следующие числовые параметры переходной характеристики:
время достижения первого максимума tm,
время регулирования tрег,
период колебаний на вершине Тв,
перерегулирование Δhm/hуст.
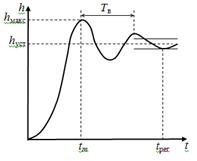
Рис.
Так как частотная характеристика замкнутой системы однозначно связана с ЛАХ и ЛФХ разомкнутой системы, то можно установить связь, по крайней мере, качественную, между логарифмическими частотными характеристиками разомкнутой системы и параметрами переходной характеристики замкнутой системы. Так, чем меньше запас устойчивости по фазе, тем больше перерегулирование и медленнее затухание колебаний на вершине. Существует следующая приближенная связь между запасом устойчивости по фазе и перерегулированием:
Δhm(в %) = 70 – Δφ(в град)
при условии, что запас устойчивости по фазе 300 < Dj < 700.
Временные параметры переходной характеристики связаны с частотой среза wср.. Чем больше частота среза, тем шире полоса пропускания замкнутой системы и меньше все временные параметры.
Как правило, системы, обладающие удовлетворительным качеством регулирования, имеют запас устойчивости по фазе от 30 до 700. Как можно обеспечить такой запас устойчивости по фазе? Если ЛАХ пересекает ось частот под наклоном -20 дБ/дек. и длина участка с таким наклоном достаточно велика, то запас устойчивости по фазе близок к 900. Такую связь можно установить, например, по логарифмическим частотным характеристикам интегрирующего звена. Во всем диапазоне частот его ЛАХ идет под наклоном –20 дБ/дек., а фазовый сдвиг равен –900. Если же ЛАХ пересекает ось частот под наклоном –40 дБ/дек. и длина участка с таким наклоном достаточно велика, то запас устойчивости по фазе близок к нулю. Поэтому такой наклон ЛАХ при пересечении оси частот нежелателен.
Наиболее легко обеспечиваются приемлемые запасы устойчивости по фазе, если ЛАХ разомкнутой системы пересекает ось частот под наклоном –20 дБ/дек. и длина участка с таким наклоном составляет около 1,5 декады. С этим участком сопрягаются участки ЛАХ с наклонами –40 или –60 дБ/дек. Можно выделить 4 типа ЛАХ в окрестности частоты среза, отличающиеся наклонами: 1) -40, -20, -40; 2) -40, -20, -60; 3) -60, -20, -40; 4) -60, -20, -60. Если ЛАХ продлить в области нижних и верхних частот без изменения наклона, то передаточная функция разомкнутой системы для каждого из этих типов ЛАХ запишется, соответственно:
|
|
| |
| (3) | ||
|
|
|
где Т1 = 1/ω1, Т2 = 1/ω2, К = 10L/20, L – значение ЛАХ на частоте ω1.
Запас устойчивости по фазе зависит как от длины участка с наклоном –20 дБ/дек., так и от соотношения сопрягающих частот ω1 и ω2 и частоты среза ωср, а также от типа ЛАХ. Для соответствующего типа ЛАХ он определяется выражениями:
Δφ1 = arctgωсрT1 – arctgωсрТ2,
Δφ2 = arctgωсрТ1 – 2arctgωсрТ2, (4)
Δφ3 = -900 + 2arctgωсрТ1 – arctgωсрТ2,
Δφ4 = -900 + 2arctgωсрТ1 – 2arctgωсрТ2.
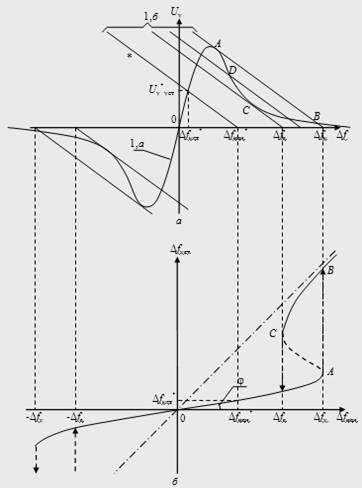
Сравним запасы устойчивости по фазе для первого и четвертого типов ЛАХ при одинаковой длительности участка с наклоном –20 дБ/дек., равном 1,5 декады (см. рис. 5). ЛФХ, соответствующая ЛАХ первого типа, получается сложением ЛФХ двух интегрирующих звеньев, форсирующего звена с постоянной времени Т1 и инерционного звена с постоянной времени Т2. ЛФХ, соответствующая ЛАХ четвертого типа, получается сложением ЛФХ трех интегрирующих звеньев, двух форсирующих и двух инерционных звеньев.
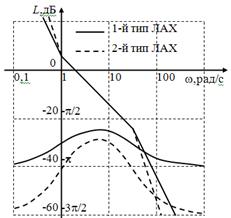
Рис.
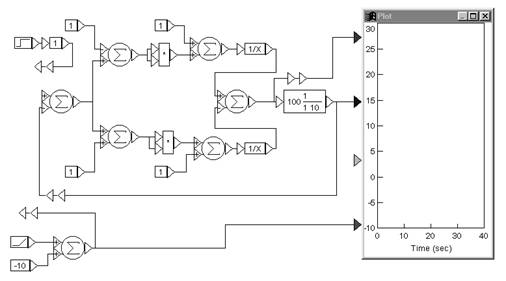
Видим, что с увеличением наклонов участков ЛАХ, сопрягаемых с участком с наклоном –20 дБ/дек., запас устойчивости по фазе становится меньше. Заметим также, что запас устойчивости по фазе уменьшается с приближением wср к w1 или w2. Для удобства сравнения процессов в системах, отличающихся друг от друга или передаточными функциями, или параметрами исследование проводится одновременно на трех моделях. Эти модели в изображении VisSim приведены на рис. 6.
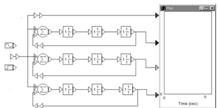
Рис.
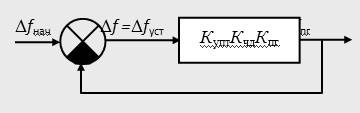
Каждая содержит три линейных звена, задаваемых передаточными функциями. При моделировании статической и астатических систем первого и второго порядка используются только два звена. При этом передаточные функции (6) целесообразно представить в виде произведения передаточных функций отдельных звеньев:
Похожие работы
... Рис. 6 Рис. 7 Схема моделирования показана на рис. 8. Рис.8 Исследование устойчивости для удобства сравнения проводится на трех моделях, отличающихся структурой или параметрами. 2.Оптимальные линейные САР Задача оптимального синтеза линейной системы авторегулирования при случайных воздействиях заключается в определении такой структуры и параметров системы, при ...
... характеристик системы в установившемся режиме составляется статическая модель. В ней отражаются только функциональные преобразования процессов. Статическая модель системы изображена на рис. 4. При ее составлении учитывалось, что для постоянного воздействия коэффициент передачи ФНЧ равен 1, а частота перестраиваемого генератора fп г = fпг0 + Dfпг, где fпг0 – частота ПГ при управляющем ...
... состояние, отнесенное к единичному возмущению на входе. Единичным возмущением считают однопроцентное изменение входной величины объекта (перемещение регулирующего органа). 2. Динамические ошибки в системах авторегулирования Системы автоматического регулирования всегда находятся под влиянием двух видов воздействий: задающего и возмущающего. Задающее воздействие определяет, каким должен ...
... и сигнализация нарушений и аварийных ситуаций с их протоколированием; Возможность дистанционного управления регулирующими исполнительными механизмами; Надежность. Для более эффективного функционирования системы автоматизации можно предъявить к Scada-пакету следующие требования: Контроль над технологическим процессом, состояние технологического оборудования и управление процессами и ...
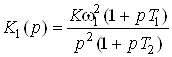 ,
, ,
,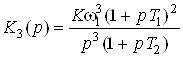 ,
,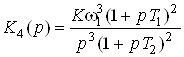 ,
,

0 комментариев