Навигация
Слабка взаємодія швидко убуває із-за масивності його переносника - векторного W або Z бозона
3. Слабка взаємодія швидко убуває із-за масивності його переносника - векторного W або Z бозона.
4. Сильна взаємодія між кварками спадає з відстанню ще набагато повільніше, а точніше, судячи з усього, його сила взагалі з відстанню не спадає; проте всі відомі частки, спостережувані у вільному стані, нейтральні відносно "сильного заряду" - кольори - оскільки або зовсім не містять кварків, або включають декілька кварків, сума кольорів яких нуль, тому в основному полі сильної взаємодії - глюонне поле - зосереджено між "кольоровими" кварками - усередині складеної частки, а його "залишкова частина", що поширюється зовні, - дуже мала і швидко спадає.
2.2 Квантовій опис атомів і резонансна взаємодія з електромагнітним полемоУ класичній електродинаміці взаємодія між зарядами здійснюється через поле: заряд породжує поле і це поле діє на інші заряди. У квантовій теорії взаємодія поля і заряду виглядає як випускання і поглинання зарядом квантів Поля — фотонів. Взаємодія ж між зарядами, наприклад між двома електронами в Квантова теорія поля є результатом їх обміну фотонами: кожен з електронів випускає фотони (кванти електромагнітного поля, що переносить взаємодію), які потім поглинаються ін. електроном. Це справедливо і для ін. фізичних полів: взаємодія в Квантова теорія поля— результат обміну квантами поля.
У цій досить наочній картині взаємодії є, проте, момент, що потребує додаткового аналізу. Поки взаємодія не почалася, кожна з часток є вільною, а вільна частка не може ні випускати, ні поглинати квантів. Дійсно, розглянемо вільну нерухому частку (якщо частка рівномірно рухається, завжди можна перейти до такої інерціальної системи відліку, в якій вона покоїться). Запасу кінетичної енергії в такої частки немає, потенційною — випромінювання енергетично неможливе.
Аби вирішити цей парадокс, потрібно врахувати, що дані частки є квантовими об'єктами і що для них істотні незрозумілостей співвідношення. Ці співвідношення зв'язують невизначеності координати частки (Dх) і її імпульсу (Dр):
![]() (1.1)
(1.1)
Є і друге співвідношення — для незрозумілостей енергії DE і специфічного часу Dt даного фізичного процесу (тобто часу, протягом якого процес протікає):
![]() . (1.2)
. (1.2)
Якщо розглядається взаємодія між частками за допомогою обміну квантами поля (це поле часто називається проміжним), то за Dt природно прийняти тривалість такого акту обміну. Питання про можливість випускання кванта вільною часткою відпадає: енергія частки, згідно (10), не є точно визначеною; за наявності ж квантового розкиду енергій DE закони збереження енергії і імпульсу не перешкоджають більш ні випусканню, ні поглинанню квантів, що переносять взаємодію, якщо лише ці кванти мають енергію ~ DE і існують протягом проміжку часу.
Проведені міркування не лише усувають вказаний вище парадокс, але і дозволяють отримати важливі фізичні виводи. Розглянемо взаємодію часток в ядрах атомів. Ядра складаються з нуклонів, тобто протонів і нейтронів. Експериментально встановлено, що поза межами ядра, тобто на відстанях, великих приблизно 10–12 см, взаємодія невідчутно, хоча в межах ядра воно свідомо велике. Це дозволяє стверджувати, що радіус дії ядерних сил має порядок L ~ 10–12 см.Саме такий дорога пролітають, отже, кванти, що переносять взаємодію між нуклонами в атомних ядрах. Час перебування квантів "в дорозі", навіть якщо прийняти, що вони рухаються з максимально можливою швидкістю (із швидкістю світла з), не може бути менше, ніж Dt. Згідно попередньому, квантовий розкид енергії DE взаємодіючих нуклонів виходить рівним DE ~. В межах цього розкиду і повинна лежати енергія кванта — переносника взаємодії. Енергія кожної частки маси m складається з її енергії спокою, рівною mc2,и кінетичної енергії, зростаючої у міру збільшення імпульсу частки. При не дуже швидкому русі часток кінетична енергія мала в порівнянні з mc2, так що можна прийняти DE " mc2. Тоді з попередньої формули виходить, що квант, що переносить взаємодії в ядрі, повинен мати масу порядку. Якщо підставити в цю формулу чисельні значення величин, то виявляється, що маса кванта ядерного поля приблизно в 200—300 разів більше маси електрона.
Такий напівякісний розгляд привів в 1935 японського фізика-теоретика Х. Юкава до передбачення нової частки; пізніше експеримент підтвердив існування такої частки, названої пі-мезоном. Цей блискучий результат значно укріпив віру в правильність квантових уявлень про взаємодію як про обмін квантами проміжного поля, віру, що зберігається в значній мірі до цих пір, не дивлячись на те, що кількісну мезонну теорію ядерних сил побудувати все ще не удалося.
Якщо розглянути 2 настільки важкі частки, що їх можна вважати класичними матеріальними крапками, то взаємодія між ними, що виникає в результаті обміну квантами маси m, приводить до появи потенційної енергії взаємодії часток, рівної
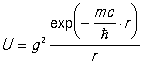 , (1.3)
, (1.3)
де r — відстань між частками, а g — так звана константа взаємодії даних часток з полем квантів, що переносять взаємодію (або інакше — заряд, відповідний даному виду взаємодії).
Якщо застосувати цю формулу до випадку, коли переносниками взаємодії є кванти електромагнітного поля — фотони, маса спокою яких m = 0, і врахувати, що замість g повинен стояти електричний заряд е, то вийде добре відома енергія кулонівської взаємодії двох зарядів: Uел = е2/r.
Графічний метод опису процесів.
Хоча в Квантовій теорії поля розглядаються типово квантові об'єкти, можна дати процесам взаємодії і перетворення часток наочні графічні зображення. Такого роду графіки вперше були введені американським фізиком Р. Фейнманом і носять його ім'я. Графіки, або діаграми, Фейнмана, зовні схожі на зображення доріг руху всіх часток, що беруть участь у взаємодії, якби ці частки були класичними (хоча ні про який класичний опис не може бути і мови). Для зображення кожної вільної частки вводять деяку лінію (яка, звичайно, є всього лише графічний символ поширення частки): так, фотон змальовують хвилястою лінією, електрон — суцільний. Інколи на лініях ставлять стрілки, поширення" частки, що умовно позначають "напрям. Нижче дані приклади таких діаграм.
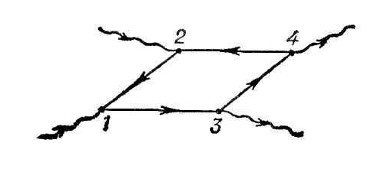
Мал..1.1 Розсіяння фотона на електроні
На мал. 1 змальована діаграма, відповідна розсіянню фотона на електроні: у початковому стані присутні один електрон і один фотон; у крапці 1 вони зустрічаються і відбувається поглинання фотона електроном; у крапці 2 з'являється (випускається електроном) новий, кінцевий фотон. Це — одна з простих діаграм Комптон-ефекту.

Рис. 1.2 Обмін фотоном між двома електронами
Діаграма на мал. 2 відображає обмін фотоном між двома електронами: один електрон в крапці 1 випускає фотон, який потім в крапці 2 поглинається другим електроном. Як вже говорилося, такого роду обмін наводить до появи взаємодії; т. о., дана діаграма змальовує елементарний акт електромагнітної взаємодії двох електронів. Складніші діаграми, відповідні такій взаємодії, повинні враховувати можливість обміну декількома фотонами; одна з них змальована на мал. 1.3.
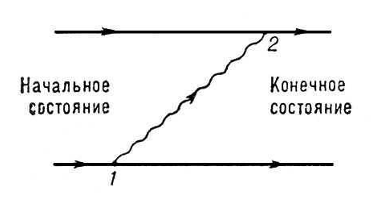
Мал..1.3. Взаємодія між фотоном і електроном
У наведених прикладах виявляється деяка загальна властивість діаграм, що описують взаємодію між електронами і фотонами: всі діаграми складаються з простих елементів — вершинних частин, або вершин, одна з яких (мал. 4) представляє випускання, а інша (мал. 5) — поглинання фотона електроном. Обоє ці процесу окремо заборонені законами збереження енергії і імпульсу. Проте якщо така вершина входить як складова частина в деяку складнішу діаграму, як це було в розглянутих прикладах, то квантова невизначеність енергії, що виникає через те, що на проміжному етапі деяка частка існує короткий час Dt, знімає енергетичну заборону.
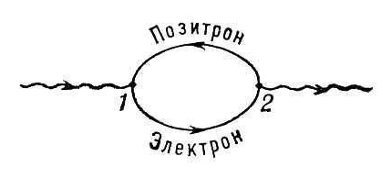
Мал.1.4 Взаємодія між позитроном та електроном
Частки, які народжуються, а потім поглинаються на проміжних етапах процесу, називаються віртуальними (на відміну від реальних часток, що існують досить тривалий час). На мал. 1 це — віртуальний електрон, що виникає в крапці 1 і зникаючий в крапці 2, на мал. 2 — віртуальний фотон і так далі Часто говорять, що взаємодія переноситься віртуальними частками. Можна декілька умовно прийняти, що частка віртуальна, якщо квантова невизначеність її енергії DE порядку середнього значення енергії частки, і її можна називати реальною, якщо DE << (для відносно повільно рухомих часток з нерівною нулю масою спокою m ця умова зведеться до нерівності DE << mc2).
Діаграми Фейнмана не лише дають наочне зображення процесів, але і дозволяють за допомогою певних математичних правил обчислювати вірогідність цих процесів. Не зупиняючись детально на цих правилах, відзначимо, що в кожній вершині здійснюється елементарний акт взаємодії, що наводить до перетворення часток (тобто до знищення одних часток і народження інших). Тому кожна з вершин дає вклад в амплітуду вірогідності процесу, причому цей вклад пропорційний константі взаємодії тих часток (або полів), лінії яких зустрічаються у вершині. У всіх приведених вище діаграмах такою константою є електричний заряд е. Чим більше вершин містить діаграма процесу, тим у вищій мірі входить заряд у відповідне вираження для амплітуди вірогідності процесу. Так, амплітуда вірогідності, відповідна діаграмам 1 і 2 з двома вершинами, квадратична по заряду (~ е2), а діаграма 3 (що містить 4 вершини) наводить до амплітуди, пропорційної четвертої міри заряду (~ е4). Крім того, в кожній вершині потрібно враховувати закони збереження (за винятком закону збереження енергії — його застосовність лімітується квантовим співвідношенням неопределенностей для енергії і часу): імпульсу (що відповідає кожній вершині акт взаємодії може статися в будь-якій точці простору отже, імпульс визначений точно), електричного заряду і так далі, а також вводити множники, залежні від спинів часток.
Вище були розглянуті лише прості види діаграм для деяких процесів. Ці діаграми не вичерпують всіх можливостей. Кожну з простих діаграм можна доповнити безконечним числом діаграм, що усе більш ускладнюються, включають все більше число вершин. Наприклад, приведену на мал. 1 "нижчу" діаграму Комптон-ефекту можна ускладнювати, вибираючи довільно пари крапок на електронних лініях і сполучаючи ці пари хвилястою фотонною лінією, оскільки число проміжних (віртуальних) фотонних ліній не лімітоване.
Взаємодія частки з вакуумом електромагнітного поля.
На приведених графіках взаємодії двох електронів (мал. 2 і 3) кожен з фотонів породжується одним і поглинається ін. електроном. Проте можливий і ін. процес: фотон, випущений електроном в крапці 1, через деякий час поглинається ним же в крапці 2. Оскільки обмін квантами обумовлює взаємодію, то такий графік також є одній з простих діаграм взаємодії, але лише взаємодії електрона з самим собою, або, що те ж саме, з власним полем. Цей процес можна також назвати взаємодією електрона з полем віртуальних фотонів, або з фотонним вакуумом (остання назва визначається тим, що реальних фотонів тут немає). Т. о., власне електромагнітне (електростатичне) поле електрона створюється випусканням і поглинанням (цим же електроном) фотонів. Такі взаємодії електрона з вакуумом обумовлюють експериментально спостережувані ефекти (що свідчить про реальність вакууму). Найзначніший з цих ефектів — випромінювання фотонів атомами. Згідно квантовій механіці, електрони в атомах розташовуються на квантових енергетичних рівнях, а випромінювання фотона відбувається під час переходу електрона з одного (вищого) рівня на іншій, що володіє меншою енергією. Проте квантова механіка залишає відкритим питання про причини таких переходів, що супроводяться так званим спонтанним ("мимовільним") випромінюванням; більш того, кожен рівень виглядає тут як сповна стійкий. Фізичною причиною нестійкості збуджених рівнів і спонтанних квантових переходів, згідно До. т. п., є взаємодія атома з фотонним вакуумом. Образно кажучи, взаємодія з фотонним вакуумом трясе, розгойдує атомний електрон — адже при випусканні і поглинанні кожного віртуального фотона електрон випробовує поштовх, віддачу; без цього електрон рухався б стійко по орбіті (ради наочності, приймемо цей напівкласичний образ). Один з таких поштовхів заставляє електрон "впасти" на стійкішу, тобто що володіє меншою енергією, орбіту; при цьому звільняється енергія, яка йде на збудження електромагнітного поля, тобто на утворення реального фотона.
Те, що взаємодія електронів з фотонним вакуумом обумовлює саму можливість переходів в атомах (і в ін. випромінюючих фотони системах), а значить, і випромінювання, — це найбільший по масштабу і за значенням ефект в квантовій електродинаміці.
2.3 «Площа» імпульсів і їх вплив на атомСпочатку коротко розглянемо моменти імпульсу електронів і атомів, визначувані по класичній електронній теорії. Отже:
1. Електрон, рухаючись по орбіті довкола ядра, володіє механічним орбітальним моментом імпульсу, де m, v – маса і швидкість електрона. При цьому вектор перпендикулярний орбіті електрона.
2. Рух електрона по орбіті відповідає протіканню деякого орбітального струму, який визначає магнітний орбітальний момент,, де I – електронний струм, S – площа витка струму (орбіти електрона). Визначимо:,, тут е – заряд електрона, T – період звернення електрона по орбіті. Тоді. Слід врахувати, що також перпендикулярний орбіті електрона, але вектора і направлені в протилежні сторони. Механічний і магнітний орбітальні моменти електрона зв'язані вираженням
Тут – це гіромагнітне (магніто–механічне) відношення орбітальних моментів електрона.
Похожие работы
... с организации экспортного отдела и заканчивают созданием международного филиала. Однако некоторые идут дальше и превращаются в транснациональные компании, высшее руководство которых уже занимается планированием маркетинга и его управлением во всемирном масштабе. Фирмы США расширяют свою международную деятельность и ищут людей, относительно свободно владеющих тем или иным иностранным языком, ...
0 комментариев