Навигация
Поняття про гіроскопічний ефект. -… хвил
4. Поняття про гіроскопічний ефект. -… хвил.
Висновки та відповіді на питання -… хвил.
Навчально-матеріальне забезпечення
Гіроскоп.
Лектор -2000.
Організаційно-методичні вказівки до проведення лекціїПеревіряється наявність курсантів та оголошується тема, мета та питання, що вивчаються, дається література.
За допомогою "Лектора-2000" пояснити та визначити формулу кінетичної енергії обертального руху твердого тіла.
Пояснити, що в обертальному русі твердого тіла мірою його інертних властивостей є момент інерції. Визначити рівняння динаміки обертального руху, пояснити за допомогою "Лектора-2000" та сформулювати закон збереження імпульсу.
Гіроскопічний ефект пояснити за допомогою гіроскопу та "Лектора-2000". Звернути увагу на його застосування.
ВступПри порівнянні законів обертального та поступального рухів спостерігається аналогія між ними, тільки в обертальному русі замість сили виступає її момент, роль маси відіграє момент інерції. В рівняння динаміки обертального руху твердого тіла відносно нерухомої осі входить його кутове прискорення. При обертальному русі аналогом імпульсу являється момент імпульсу.
Закони збереження моменту імпульсу - фундаментальний закон природи. Він пов’язаний з певною властивістю симетрії простору - його ізотропністю, тобто з інваріантністю фізичних законів відносно вибору напрямку осей координат системи відліку.
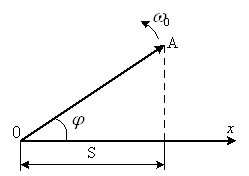
Момент сили. кінетична енергія обертового тілаНехай тіло обертається під дією сили F. Довжина перпендикуляру, опущеного з вісі обертання на лінію дії сили називається плечем сили. Добуток сили на плече називається моментом сили:
![]() (1)
(1)
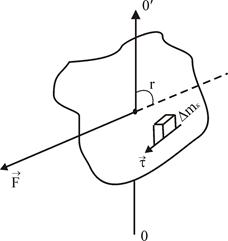
Рис.1
Будь-який елемент маси обертового тіла має лінійну швидкість ![]() і отже, він має кінетичну енергію
і отже, він має кінетичну енергію
![]() .
.
Використавши співвідношення:
![]()
![]()
Знаходимо
![]() ,
,
але ![]() являє собою момент інерції елемента маси. Тому маємо:
являє собою момент інерції елемента маси. Тому маємо:
![]() (2)
(2)
Кінетична енергія всього тіла буде дорівнювати сумі кінетичних енергій всіх елементів мас:
![]() .
.
Величина ![]() визначає собою момент інерції всього тіла відносно даної вісі обертання. Тому кінетична енергія обертового тіла рівна:
визначає собою момент інерції всього тіла відносно даної вісі обертання. Тому кінетична енергія обертового тіла рівна:
![]() . (3)
. (3)
Якщо тіло одночасно з обертанням рухається поступально, то його повна кінетична енергія рівна:
![]() , (4)
, (4)
де n - швидкість руху центрам мас тіла.
Момент інерції тіла відносно даної вісі характеризує інерційні властивості тіла при обертовому рухові навколо даної вісі.
Момент інерції. рівняння динаміки обертового рухуПри порівнянні законів поступового і обертального руху між ними існує аналогія. Так формули кінетичної енергії мають однаковий вигляд, але при обертанні тіл роль маси відіграє момент інерції. Яка ж величина грає роль сили?
Розглянемо обертання твердого тіла навколо вісі ![]() (рис.1)
(рис.1)
Нехай на елемент маси ![]() діє сила
діє сила ![]() . Елемент маси обертається з лінійною швидкістю
. Елемент маси обертається з лінійною швидкістю ![]() . Тоді із 2 закону Ньютона маємо:
. Тоді із 2 закону Ньютона маємо:
![]() ;
; ![]() ;
; ![]() (5)
(5)
Тому знаходимо:
![]() .
.
Домноживши обидві частини останнього рівняння на ![]() одержимо:
одержимо:
![]() .
.
Просумуємо ці рівняння для всіх елементів тіла:
![]() .
.
Величини ![]() являє собою сумарний обертовий момент, що діє на тіло, а величина
являє собою сумарний обертовий момент, що діє на тіло, а величина ![]() - момент інерції тіла. Тоді маємо:
- момент інерції тіла. Тоді маємо:
![]() (6)
(6)
Рівняння (6) називається основним рівнянням динаміки обертового руху. Формулюється так: момент сили, що діє на тіло, дорівнює добутку моменту інерції тіла на кутове прискорення. Рівняння (6) називають 2 законом Ньютона для обертового руху.
Момент імпульсу. закон збереження моменту імпульсу
З рівняння (5) маємо:
![]() .
.
Домноживши обидві частини цього рівняння на ![]() , одержимо:
, одержимо:
![]() .
.
При постійних ![]()
![]() можна записати так:
можна записати так:
![]() . (7)
. (7)
Добуток імпульсу елемента маси ![]() на відстань від вісі обертання до елемента маси називається моментом імпульсу.
на відстань від вісі обертання до елемента маси називається моментом імпульсу.
![]() (8)
(8)
Просумуємо рівняння виду (7) для всіх елементів тіла. Знайдемо:
![]() ;
;
Дій ![]() (9)
(9)
Де ![]() сумарний обертовий момент, що діє на тіло.
сумарний обертовий момент, що діє на тіло.
![]() - момент імпульсу всього тіла (момент кількості руху). Можна записати так:
- момент імпульсу всього тіла (момент кількості руху). Можна записати так:
![]() ,
,
або L = Iw, або ![]() (10)
(10)
Момент імпульсу - це вектор, направлений по вісі обертання у відповідності з правилом правого гвинта. Таким чином, вектор моменту імпульсу співпадає з напрямом вектора кутової швидкості.
Таким чином, момент імпульсу тіла дорівнює добутку моменту інерції тіла на кутову швидкість. Рівняння (9) можна записати так:
![]() . (11)
. (11)
або у векторній формі
![]() .
.
Це рівняння називається рівнянням моментів.
Якщо на тіло діють сили або сумарний обертовий момент дорівнює нулю, тоді маємо:
![]() або
або ![]()
В цьому і полягає закон збереження моменту імпульсу. Його можна записати так:
![]() (12)
(12)
Момент імпульсу замкнутої системи зберігається, тобто, не змінюється з плином часу.
Цей закон використовується спортсменами при виконанні стрибка через голову.
Роль імпульсу тіла при обертальному рухові відіграє момент імпульсу. Момент імпульсу пов’язаний з певною властивістю симетрії простору - його ізотропністю, тобто з інваріантністю фізичних законів відносно вибору напрямків вісей координат системи відліку (відносно повороту замкнутої системи в просторі на будь-який кут).
| Поступальний рух | Обертальний рух |
| Маса m | Момент інерції J |
| Шлях S | Кут оберту j |
| Швидкість | Кутова швидкість |
| Імпульс | Момент імпульсу |
| Прискорення | Кутове прискорення |
| Рівнодіюча зовнішніх сил | Сума моментів зовнішніх сил |
| Основне рівняння динаміки | Основне рівняння динаміки |
| Робота FdS | Робота обертання Mdj |
| Кінетична енергія | Кінетична енергія обертання |
Закон збереження моменту імпульсу - фундаментальний закон природи.
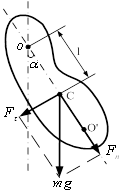
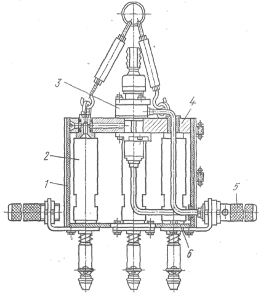
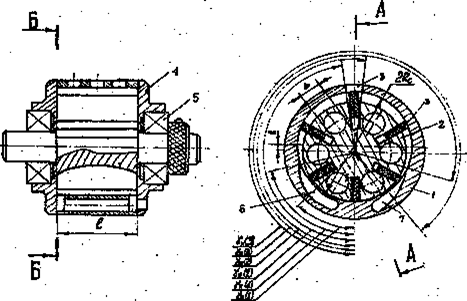
Поняття про гіроскопічний ефектРозглянемо один з різновидів гіроскопів - гіроскоп на карданному підвіччі (рис.2). Дисковидне тіло - гіроскоп закріплене на вісі АА, яка може обертатися навколо горизонтальної вісі ВВ, яка в свою чергу, може обертатися навколо вертикальної вісі СС. Всі 3 вісі перетинаються в одній точці Д, що є центром мас гіроскопа і зостаючись нерухомою, вісь гіроскопу може прийняти будь-який напрям в просторі. Силами тертя в підшипниках всіх трьох вісей і моментом руху кілець нехтуємо: тертя в підшипниках мале, то поки гіроскоп нерухомий, його вісі можна надати будь-який напрям. Якщо почати швидко обертати гіроскоп - (наприклад, за допомогою намотаної на вісі мотузочки) і обертати його підставку, то вісь гіроскопа зберігає своє положення в просторі незмінним. Це можна пояснити за допомогою основного закону динаміки обертального руху. Для гіроскопа, що вільно обертається, сила тяжіння не може змінити орієнтацію вісі його обертання. Бо ця сила прикладена до центру мас (центр обертання Д співпадає з центром мас), а момент сили тяжіння відносно закріпленого центра має дорівнювати нулю. Моментом сили тертя ми нехтуємо. Тому, якщо момент зовнішніх сил відносно його закріпленого центра мас дорівнює нулю, то як слідує з рівняння (11).
![]() ,
,
тобто момент кількості руху гіроскопа зберігає своє значення і напрям в просторі.
Незмінним буде і момент кількості руху гіроскопа відносно вісі обертання, рівний L = Jw і напрямлений вздовж вісі обертання. Отже, при даній умові вісь обертання гіроскопа зберігає своє положення в просторі.
Щоб вісь гіроскопа змінила свій напрям в просторі необхідно, згідно з (11), щоб момент зовнішніх сил, що прикладені до гіроскопа, що обертається відносно його центра мас, відмінний від нуля, то одержуємо явище, що має назву гіроскопічного ефекту. Він полягає в тому, що під дією пара сили F, прикладеної до вісі обертання гіроскопа, вісь гіроскопа (рис.2) обертається навколо прямої ![]() , а не навколо прямої
, а не навколо прямої ![]() , як це вважалося б природним на перший погляд (
, як це вважалося б природним на перший погляд (![]() лежать в площині креслення, а
лежать в площині креслення, а ![]() і сили F перпендикулярний до неї).
і сили F перпендикулярний до неї).
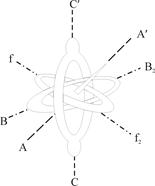
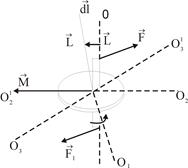
Рис.2 Рис.3
Гіроскопічний ефект пояснюється таким чином. Момент М пари сил F напрямлений вздовж прямої ![]() . За час
. За час ![]() момент імпульсу L гіроскопа одержує приріст
момент імпульсу L гіроскопа одержує приріст ![]() (напрям
(напрям ![]() співпадає з напрямом
співпадає з напрямом ![]() ) і стане рівним
) і стане рівним ![]() . Напрям вектора L співпадає з новим напрямом вісі обертання гіроскопа повернуться навколо прямої
. Напрям вектора L співпадає з новим напрямом вісі обертання гіроскопа повернуться навколо прямої ![]() . Якщо час дії сили малий, то хоч момент сил
. Якщо час дії сили малий, то хоч момент сил ![]() великий, зміна моменту імпульсу
великий, зміна моменту імпульсу ![]() гіроскопа буде теж малим. Тому сила практично не призводить до зміни орієнтації вісі обертання гіроскопа в просторі. Для її зміни потрібно прикладати сили довгий час.
гіроскопа буде теж малим. Тому сила практично не призводить до зміни орієнтації вісі обертання гіроскопа в просторі. Для її зміни потрібно прикладати сили довгий час.
Якщо вісь гіроскопа закріплена підшипниками то в наслідок гіроскопічного ефекту виникають так звані гіроскопічні сили, що діють на опори, в яких обертається вісь гіроскопа. Їхню дію необхідно враховувати при конструюванні пристроїв, що містять в собі масивні складові частини, що швидко обертаються (наприклад, підшипники парових турбін на кораблях).
Гіроскопи застосовуються в різних гіроскопічних навігаційних приладах (гірокомпас, гірогоризонт і т.д.). Інше важливе застосування гіроскопів - підтримання заданого напряму руху транспортних засобів, наприклад судна і літака (автопілот) і ін. При будь-якому відхиленні від курсу внаслідок якихось впливів (хвиль, порив вітру і т.д.) положення вісі гіроскопа в просторі зберігається. Отже, вісь гіроскопа разом з рамами карданового підвісу обертається відносно пристрою, що рухається. Оберт рам карданового підвісу за допомогою певних пристроїв містить рулі керування, які повертають рух до заданого курсу. Подібним же чином гіроскопи можуть застосовуватись для автоматичного керування рухом снарядів, що само рухаються.
Вперше гіроскоп застосований французьким фізиком Фуко (1819 - 1868 рр) для доказу обертання Землі.
ВисновкиОсновна задача динаміки обертального руху твердого тіла - визначити кутові координати точок обертового тіла в будь-який момент часу за відомими початковими кутовими координатами, кутовою швидкістю і моментом зовнішніх сил, які діють на тіло.
Моментом інерції тіла відносно осі називається величина, що дорівнює сумі моментів інерції всіх матеріальних точок, на які можна уявно поділити тіло, відносно даної осі. Якщо тіло бере участь одночасно в обертальному і поступальному русі, то його кінетичну енергію визначають за формулою:
![]() .
.
Другий закон динаміки обертального руху твердого тіла визначається формулою:
![]()
Момент імпульсу ![]() замкнутої системи тіл відносно будь-якої нерухомої осі залишається сталим.
замкнутої системи тіл відносно будь-якої нерухомої осі залишається сталим.
Навчальна література
1. Кучерук І.М., Горбачук І.Г. Загальна фізика. Електроніка і магнетизм. - К.: Вища школа, 1990.
2. Савельев И.В. Курс физики, т.3, Квантовая физика. - М.: 1989.
3. Трофимова Т.И. Курс физики, - М.: Высшая школа, 1985, 432 с.
4. Бушок Г.Ф., Левандовський В.В., Півень Г.Ф. Курс фізики (Оптика. Фізика атома і атомного ядра. Молекулярна фізика і термодинаміка), т.2,-Київ.: Либідь, 2001, - 421 с.
Похожие работы
... R.A. Naryshkin. Collision integral of highly excited gas // 3rd International Conference PLM MP. Abstracts. – Kyiv, 2005 (May 27–31). – P. 56 (2-6. O.). АНОТАЦІЇ Наришкін Р.О. Гідродинамічна нестійкість вихрового руху в системах з об’ємним стоком речовини. — Рукопис. Дисертація на здобуття наукового ступеня кандидата фізико-математичних наук за спеціальністю 01.04.02 — теоретична фізика.— ...
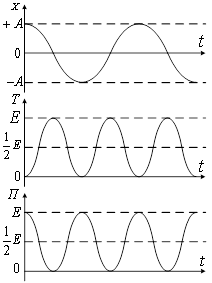
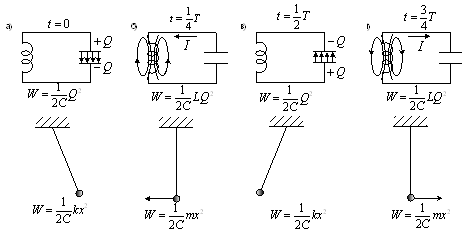
... коливань якого збігається з періодом коливань даного фізичного маятника. 4. Вільні гармонійні коливання у коливальному контурі Серед різних електричних явищ особливе місце займають електромагнітні коливання, при яких фізичні величини (заряди, струми, електричні і магнітні поля) періодично змінюються. Для виникнення і підтримування електромагнітних коливань необхідні певні системи, найпрості ...
... для систем, частинок з антисиметричними хвильовими функціями, тобто до ферміонів. 2.2.3. Розподіл електронів за станами. Періодична система елементів. Сукупність електронів, які перебувають у всіх можливих станах з однаковим значенням головного квантового числа n, утворює електронну оболонку (електронний шар). Енергетичні шари прийнято позначати великими латинськими літерами відповідно до ...
... В) полив прилеглої території - - 0,3 2. Госп-побутова та виробнича каналізація (К1; К3) 5,04 1,26 2,86 1.3 Розрахунок виробничої програми по централізованому обслуговуванню маршрутних транспортних засобів 1.3.1 Коригування нормативів технічного обслуговування та ремонту рухомого складу Відповідно до завдання нам необхідно провести коригування нормативів технічного ...

0 комментариев