Навигация
Механічні й електромагнітні коливання
РЕФЕРАТ
на тему:”Механічні й електромагнітні коливання”
План
1. Гармонічні коливання і їх характеристики
2. Механічні гармонічні коливання
3. Гармонічний осцилятор. Пружинний, фізичний і математичний маятники
4. Вільні гармонійні коливання в коливальному контурі
1. Гармонічні коливання і їх характеристики
Коливаннями називаються рухи або процеси, які характеризуються певною повторюваністю в часі. Коливальні процеси широко поширені в природі й техніці, наприклад, коливання маятника годинника, змінний електричний струм і т.д. При коливальному русі маятника змінюється координата його центра мас, у випадку змінного струму - коливаються напруга й струм у ланцюзі. Фізична природа коливань може бути різною, тому розрізняють коливання механічні, електромагнітні й ін. Однак різні коливальні процеси описуються однаковими характеристиками й однаковими рівняннями. Звідси випливає доцільність єдиного підходу до вивчення коливань різної фізичної природи.
Коливання будуть вільними (або власними), якщо вони відбуваються за рахунок деякої енергії, переданої коливальній системі в початковий момент часу, при відсутності в наступні моменти часу будь-яких зовнішніх впливів на цю систему. Найпростішими коливаннями є гармонічні коливання, при яких коливна величина змінюється з часом за законом косинуса або синуса. Вивчення гармонічних коливань важливе з двох причин:
1) коливання, які зустрічаються у природі й техніці, при певних наближеннях є гармонічними;
2) різні періодичні процеси (процеси, які повторюються через рівні проміжки часу), можна подавати як суперпозицію гармонічних коливань.
Гармонічні коливання деякої фізичної величини х описуються таким рівнянням
![]() (1)
(1)
де А- максимальне значення коливної величини x, яке називається амплітудою коливань; ![]() - колова, або циклічна частота; φ - початкова фаза коливань для моменту часу t = 0;
- колова, або циклічна частота; φ - початкова фаза коливань для моменту часу t = 0; ![]() - фаза коливань для довільного моменту часу t. Так як косинус змінюється в межах від +1 до -1, то х може набувати значень від +А до -А.
- фаза коливань для довільного моменту часу t. Так як косинус змінюється в межах від +1 до -1, то х може набувати значень від +А до -А.
Певні стани системи в процесі гармонічних коливань повторюються
через однаковий проміжок часу Т, який називається періодом коливань. За цей час фаза коливання зростає на 2π, тобто
![]()
звідки
![]() (2)
(2)
Величина, обернена до періоду коливань
![]() (3)
(3)
виконана коливною системою за одиницю часу, називається частотою коливань. Прирівнюючи (2) і (3), одержимо
ω0 = 2![]() .
.
Одиницею частоти є герц (Гц), це частота такого періодичного процесу, при якому за 1 с відбувається одне повне коливання.
Запишемо першу й другу похідні фізичної величини х гармонічного коливання, тобто визначимо швидкість і прискорення коливання:
![]() (4)
(4)
![]() (5)
(5)
тобто маємо гармонічні коливання тієї ж циклічної частоти. Амплітуди величин (4) і (5) відповідно дорівнюють ![]() і
і ![]() . Фаза швидкості (4) відрізняється від фази фізичної величини (1) на π/2, а фаза прискорення (5) відрізняється від фази фізичної величини (1) на π.
. Фаза швидкості (4) відрізняється від фази фізичної величини (1) на π/2, а фаза прискорення (5) відрізняється від фази фізичної величини (1) на π.
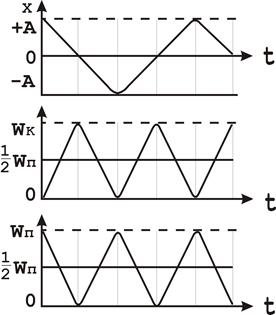
Отже, у моменти часу, коли х = 0, ![]() має найбільші значення; коли ж x досягає максимальних від’ємних значень то в ці моменти часу
має найбільші значення; коли ж x досягає максимальних від’ємних значень то в ці моменти часу ![]() будуть мати найбільші додатні значення (рис. 1).
будуть мати найбільші додатні значення (рис. 1).
З рівняння (5) одержуємо диференціальне рівняння гармонічних коливань (де враховано, що х = Acos (ωοt + φ)),
![]() . (6)
. (6)
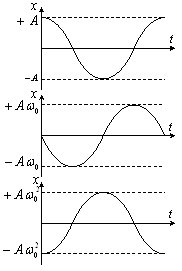
Рис. 1
Таким чином, розв’язком диференціального рівняння (6) є вираз (1).
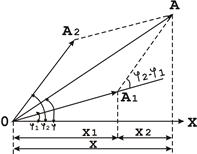
Гармонічні коливання можна зобразити графічно за допомогою методу обертання вектора амплітуди, або методу векторних діаграм. Для цього з довільної точки О, взятої на осі х, під кутом φ, який дорівнює початковій фазі коливання, відкладається вектор ![]() , модуль якого дорівнює амплітуді А гармонічного коливання (рис. 2).
, модуль якого дорівнює амплітуді А гармонічного коливання (рис. 2).
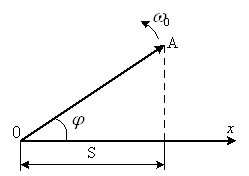
Рис. 2
Якщо цей вектор привести до обертання з кутовою швидкістю ![]() то проекція кінця вектора буде переміщуватися по осі x і набувати значень від -А до + А, а коливна величина буде змінюватися з часом за законом х = Acos(ωοt + φ). У фізиці часто застосовується інший метод, який відрізняється від методу обертання вектора амплітуди лише за формою. У цьому методі коливну величину подають комплексним числом. Відповідно до формули Ейлера, для комплексних чисел
то проекція кінця вектора буде переміщуватися по осі x і набувати значень від -А до + А, а коливна величина буде змінюватися з часом за законом х = Acos(ωοt + φ). У фізиці часто застосовується інший метод, який відрізняється від методу обертання вектора амплітуди лише за формою. У цьому методі коливну величину подають комплексним числом. Відповідно до формули Ейлера, для комплексних чисел
![]() (7)
(7)
де ![]() - уявна одиниця. Тому рівняння гармонічного коливання (1) можна записати також в експонентній формі так:
- уявна одиниця. Тому рівняння гармонічного коливання (1) можна записати також в експонентній формі так:
![]() (8)
(8)
Права частина рівняння (8) є рівнянням гармонічних коливань.
Похожие работы
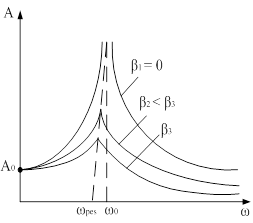
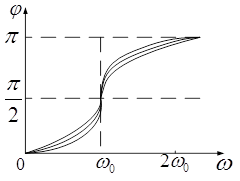
... і фаза вимушених коливань (механічних і електромагнітних). Резонанс. Резонансні криві. Парамет-ричний резонанс Розглянемо залежність амплітуди А вимушених механічних або електромагнітних коливань від частоти ω. Механічні й електромагнітні коливання будемо розглядати одночасно, називаючи коливну величину або зміщенням (х) коливного тіла від положення рівноваги, або зарядом (Q) конденсатора. ...
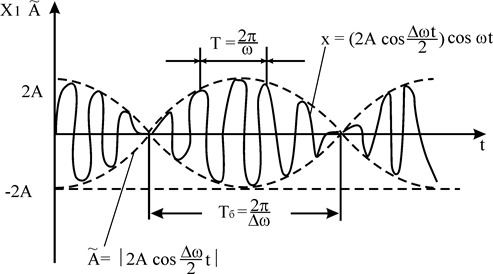
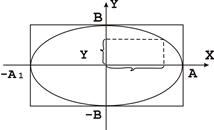
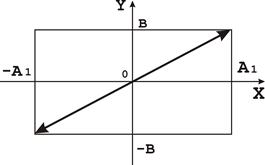
... і гармонічних коливань однакового напрямку і однакової частоти- результуюче коливання є гармонічним тієї ж частоти. В результаті додавання гармонічних коливань близької частоти, однаково спрямованих, одержується биття. За допомогою фігур Ліссажу визначається невідома частота. ЗАТУХАЮЧІ КОЛИВАННЯ ЗМІСТ Вступ. 1. Затухаючі коливання. Диференціальне рівняння затухаючих механічних та ...
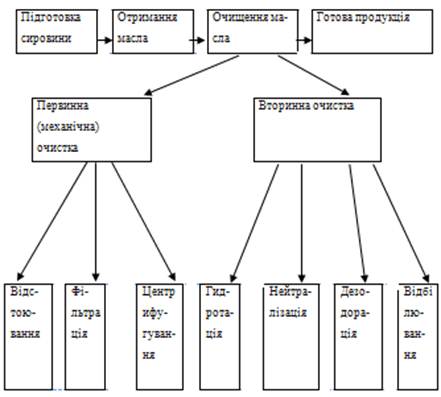
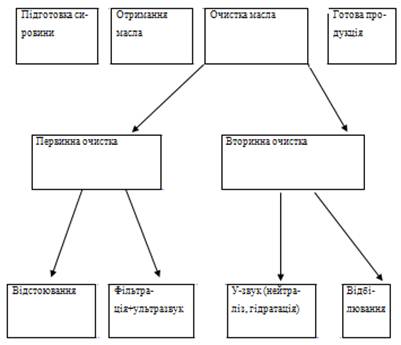
... кредиту 2 роки Погашення кредиту за 2 роки Джерело виплат прибуток Гарантії майно Висновки і пропозиції до курсової роботи На початку розробки курсового проекту я користувався такими гіпотезами як: - корисна дія електромагнітних коливань для процесу фільтрації як невід’ємної складової процесу очищення соняшникової олії; - прискорення та полегшення процесу гідратації соняшникової ол
... івнює , а в домішкових напівпровідниках має зміст енергії іонізації донорів чи акцепторів. Отже, питома електропровідність напівпровідників експоненційно збільшується з ростом температури, чим останні принципово відрізняються від металів. Розділ VII. Фізика ядра та елементарних часток. § 7.1. Склад і характеристики ядра Ядро атома, як центральну позитивно заряджену масивну частину атома, ...

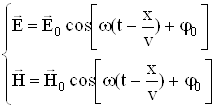

0 комментариев