Навигация
Состояние проблемы и постановка задачи
2. Состояние проблемы и постановка задачи.
2.1 Газокинетические процессы в дисперсной системе 2.1.1 Непрерывная и дискретная динамика.
Исследование динамики аэрозолей в среде (в том числе в воздухе), необходимо определить, с точки зрения процессов переноса. В свободно - молекулярном режиме молекулы среды перемещаются по прямой, пока не столкнутся с другой молекулой, после чего, молекула изменяет направление, до того момента, пока вновь не столкнётся с другой молекулой, и так далее. Среднее расстояние, пройденное молекулой между столкновениями с другими молекулами, называется длиной свободного го пробега. В зависимости от относительного размера частицы, находящейся в среде и средней длины свободного пробега, отличают два случая.
· Если размер частицы намного больше, чем средняя длина свободного пробега окружающих молекул, система ведет себя, как непрерывная среда. Движение такой частицы подчиняется законам диффузии.
· В другом случае, если частица намного меньше, чем средняя длина свободного пробега окружающих молекул, то она (частица) ведёт себя как большая молекула. В этом случае говорят о свободно - молекулярный режим.
Ключевой в нашем случае, безразмерный параметр, который определяет характерные свойства среды относительно частицы, - число Кнудсена.
 (2.1)
(2.1)
где λ- длина свободного пробега, D – диаметр частицы, а R, соответственно, её радиус. Таким образом, число Кнудсена - отношение двух метрических параметров.
Прежде, чем обсуждать роль числа Кнудсена, мы должны рассмотреть вычисление средней длины свободного пробега для пара. Так же необходимо вычислить среднюю длину свободного пробега для чистого газа и для газов, составленных из смесей нескольких компонентов. Заметим, что воздух, в основном, состоит из смеси кислорода с азотом, однако общепринято говорить о средней длине свободного пробега воздуха, ![]() , как будто воздух - отдельная химическая разновидность.
, как будто воздух - отдельная химическая разновидность.
Начнём с самого простого случая, когда частица, находится в чистом газе B. Если нас интересует природа газа – носителя, то мы должны рассчитать средний путь свободного пробега, который появляется при определении числа Кнудсена, - ![]() . Индекс обозначает, что мы интересуемся столкновениями молекул B друг с другом. Длина свободного пробега была определена, как среднее расстояние, которое проходит молекула B между столкновениям с другой молекулой B. Средняя скорость газовых молекул B, -
. Индекс обозначает, что мы интересуемся столкновениями молекул B друг с другом. Длина свободного пробега была определена, как среднее расстояние, которое проходит молекула B между столкновениям с другой молекулой B. Средняя скорость газовых молекул B, - ![]() (Moore, 1962):
(Moore, 1962):
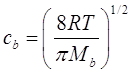 , (2.2)
, (2.2)
где MB - молекулярный вес молекулы B. Отметим, что большие молекулы перемещаются более медленно, в то время как средняя скорость газа увеличивается с температурой. Средняя скорость молекулы азота при температуре 298К, согласно (8.2) равна 474 м/c, а кислорода – 444 м/c.
Давайте оценим то, что случается с молекулой B в течение единицы времени, скажем, секунды. В течение этой секунды молекула перемещается, в среднем, на расстояние, равное этому промежутку времени (секунда), умноженному на скорость молекулы. Если в течение той секунды молекула подвергается некоторому числу столкновений – Zbb, то ее средняя длина свободного пробега будет равна, по определению,
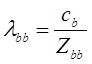 (2.3)
(2.3)
Таким образом, чтобы вычислить среднюю длину свободного пробега молекулы, мы должны сначала вычислить число столкновений Zbb. Пускай, ![]() - диаметром молекулы B. За 1 секунду молекула перемещается на дистанцию
- диаметром молекулы B. За 1 секунду молекула перемещается на дистанцию ![]() и сталкивается со всеми молекулами, центры которых находятся в цилиндре радиуса
и сталкивается со всеми молекулами, центры которых находятся в цилиндре радиуса ![]() и высоты
и высоты ![]() . Отметим, что две молекулы диаметра
. Отметим, что две молекулы диаметра ![]() сталкиваются тогда и только тогда, когда расстояние между их центрами
сталкиваются тогда и только тогда, когда расстояние между их центрами ![]() . Если
. Если ![]() - число молекул B в единице объёма, то число молекул в вышеупомянутом цилиндре -
- число молекул B в единице объёма, то число молекул в вышеупомянутом цилиндре - ![]() . Итак, мы вычислили число столкновений, предполагающих, что одна молекула B перемещается, в то время как остальные молекулы неподвижны, в результате чего недооценили частоту столкновений. Вообще, все частицы перемещаются в случайных направления, и мы должны описать это движение, оценивая их относительную скорость. Если две частицы перемещаются в противоположных направлениях, их относительная скорость - 2
. Итак, мы вычислили число столкновений, предполагающих, что одна молекула B перемещается, в то время как остальные молекулы неподвижны, в результате чего недооценили частоту столкновений. Вообще, все частицы перемещаются в случайных направления, и мы должны описать это движение, оценивая их относительную скорость. Если две частицы перемещаются в противоположных направлениях, их относительная скорость - 2![]() . Если они двигаются в одном направлении, их относительная скорость - ноль, в то время как при движении под углом в 90° их относительная скорость -
. Если они двигаются в одном направлении, их относительная скорость - ноль, в то время как при движении под углом в 90° их относительная скорость - ![]() . Можно доказать, что последняя ситуация определяет среднее число, таким образом:
. Можно доказать, что последняя ситуация определяет среднее число, таким образом:
![]() (2.4)
(2.4)
и средняя длина свободного пробега:
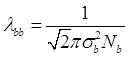 (2.5)
(2.5)
Видно, что чем больше размер молекулы, ![]() , и выше газовая концентрация, тем меньшее значение принимает средняя длина свободного пробега.
, и выше газовая концентрация, тем меньшее значение принимает средняя длина свободного пробега.
К сожалению, даже притом, что (2.5) обеспечивает достаточно неплохую зависимость длины свободного пробега от газовой концентрации и размера молекулы, она не удобна для использования, потому что необходимо знать диаметр молекулы ![]() , так же, большинство молекул вовсе не являются сферическими. Окончательно всё усугубляет то, что средняя длина свободного пробега газа не может быть измерена непосредственно. Однако, она может быть теоретически связана с измеримыми газовыми макроскопическими свойствами, типа вязкости, коэффициента теплопроводности, или молекулярного коэффициента диффузии. Таким образом, можно использовать вышеупомянутые газовые свойства, чтобы оценить теоретически среднюю длину свободного пробега в газе. Например, длина свободного пробега чистого газа может быть связана с газовой вязкостью, соотношением, что следует из кинетической теории газов:
, так же, большинство молекул вовсе не являются сферическими. Окончательно всё усугубляет то, что средняя длина свободного пробега газа не может быть измерена непосредственно. Однако, она может быть теоретически связана с измеримыми газовыми макроскопическими свойствами, типа вязкости, коэффициента теплопроводности, или молекулярного коэффициента диффузии. Таким образом, можно использовать вышеупомянутые газовые свойства, чтобы оценить теоретически среднюю длину свободного пробега в газе. Например, длина свободного пробега чистого газа может быть связана с газовой вязкостью, соотношением, что следует из кинетической теории газов:
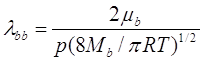 (2.6)
(2.6)
где ![]() - газовая вязкость, p - газовое давление, и MB - молекулярный вес B.
- газовая вязкость, p - газовое давление, и MB - молекулярный вес B.
Таким образом, для стандартных атмосферных условий, если диаметр частицы является большим, чем приблизительно 0.2![]() , Kn < 1, и с точки зрения атмосферных свойств, частица находится в непрерывном режиме. В этом случае применимы уравнения механики сплошной среды. Когда диаметр частицы является меньшим, чем 0.01
, Kn < 1, и с точки зрения атмосферных свойств, частица находится в непрерывном режиме. В этом случае применимы уравнения механики сплошной среды. Когда диаметр частицы является меньшим, чем 0.01![]() , частица существует в более или менее разреженной среде, и ее свойства переноса должны быть получены из кинетической теории газов. Этот режим, когда Kn >> 1 называют свободно молекулярным режимом. Промежуточное звено, когда размер частицы заключён между этими двумя значениями (0.01
, частица существует в более или менее разреженной среде, и ее свойства переноса должны быть получены из кинетической теории газов. Этот режим, когда Kn >> 1 называют свободно молекулярным режимом. Промежуточное звено, когда размер частицы заключён между этими двумя значениями (0.01 ![]() и 0.2
и 0.2![]() ) называют переходным режимом.
) называют переходным режимом.
Теперь перейдём к рассмотрению более интересного случая – определению длины свободного пробега газа в бинарной смеси. Если мы интересуемся диффузией молекулы пара к частице, которые содержатся в фоновом газе B (например, в воздухе), тогда описание диффузионного процесса, зависит от значения числа Кнудсена, определение которого основано на среднем длине свободного пробега ![]() . Отметим, что, если концентрация молекул A – на несколько порядков ниже чем концентрация молекул фонового газа B (воздух), столкновениями между молекулами А можно пренебречь. Столкновения между молекулами А и B фактически равны общему количеству столкновений. Число Кнудсена определяют так:
. Отметим, что, если концентрация молекул A – на несколько порядков ниже чем концентрация молекул фонового газа B (воздух), столкновениями между молекулами А можно пренебречь. Столкновения между молекулами А и B фактически равны общему количеству столкновений. Число Кнудсена определяют так:
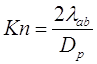 (2.7)
(2.7)
теперь мы должны оценить![]() . Джинс (Jeans) показал, что средняя длина свободного пробега молекул A,
. Джинс (Jeans) показал, что средняя длина свободного пробега молекул A, ![]() , в бинарной смеси A и B - (Davis, 1983)
, в бинарной смеси A и B - (Davis, 1983)
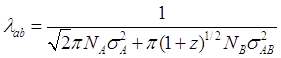 (2.8)
(2.8)
где ![]() и
и ![]() - молекулярные концентрации частиц A и B,
- молекулярные концентрации частиц A и B, ![]() и
и ![]() - ударные диаметры для бинарных столкновений между молекулами A и молекулами A и B, соответственно, где
- ударные диаметры для бинарных столкновений между молекулами A и молекулами A и B, соответственно, где
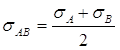 (2.9)
(2.9)
и ![]() - отношение молекулярных масс A и B. Первый член в знаменателе (8.9) отвечает за столкновения между молекулами А, в то время как второй - за столкновения между молекулами A и молекулами B. Если концентрация молекул A очень низка (в действительности, в атмосферных приложениях, так и есть),
- отношение молекулярных масс A и B. Первый член в знаменателе (8.9) отвечает за столкновения между молекулами А, в то время как второй - за столкновения между молекулами A и молекулами B. Если концентрация молекул A очень низка (в действительности, в атмосферных приложениях, так и есть), ![]() и (8.9) может быть упрощена, фактическим пренебрежением столкновениями между молекулами А:
и (8.9) может быть упрощена, фактическим пренебрежением столкновениями между молекулами А:
 (2.10)
(2.10)
Отметим, что молекулярная концентрация ![]() может легко быть вычислена из уравнения Клайперона
может легко быть вычислена из уравнения Клайперона ![]() , где p - давление системы. Средний{скупой} путь свободного пробега газа проекции прямой на заднем плане газ не зависит от концентрации непосредственно. Это не удивительно, поскольку мы предположили, что концентрация A настолько низка, что молекулы никогда не сталкиваются и не взаимодействуют друг с другом. Далее мы сосредотачиваемся на взаимодействиях частиц с единственным газом - воздухом, где средняя длина свободного пробега задана формулой (2.6).
, где p - давление системы. Средний{скупой} путь свободного пробега газа проекции прямой на заднем плане газ не зависит от концентрации непосредственно. Это не удивительно, поскольку мы предположили, что концентрация A настолько низка, что молекулы никогда не сталкиваются и не взаимодействуют друг с другом. Далее мы сосредотачиваемся на взаимодействиях частиц с единственным газом - воздухом, где средняя длина свободного пробега задана формулой (2.6).
Неустановившаяся диффузия молекул вида A к поверхности частицы радиуса ![]() :
:
 (2.11)
(2.11)
где c(r,t) – концентрация молекул А, а ![]() - молярный поток (количество молей падающих на единицу площади в единицу времени) в любом радиальном положении r. Это уравнение - просто выражение массового баланса в бесконечно малой сферической ячейке, вокруг частицы. Молярный поток молекул A дается согласно закону Фика (Бирд и др., 1960),
- молярный поток (количество молей падающих на единицу площади в единицу времени) в любом радиальном положении r. Это уравнение - просто выражение массового баланса в бесконечно малой сферической ячейке, вокруг частицы. Молярный поток молекул A дается согласно закону Фика (Бирд и др., 1960),
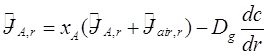 (2.12)
(2.12)
где ![]() - молекулярная фракция частиц A,
- молекулярная фракция частиц A, ![]() - радиальный поток воздуха в положении r, и
- радиальный поток воздуха в положении r, и ![]() - коэффициент диффузии молекул А в воздухе. Так как выделенных направлений нет,
- коэффициент диффузии молекул А в воздухе. Так как выделенных направлений нет, ![]() во всех r. Принимая во внимание предположение, применимое в большинстве атмосферных состояний -
во всех r. Принимая во внимание предположение, применимое в большинстве атмосферных состояний - ![]() ,
,![]() (2.12) может быть переписана как
(2.12) может быть переписана как
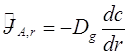 (2.13)
(2.13)
Теперь, комбинируя (2.11) и (2.13), получим:
![]()
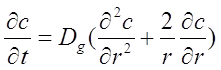 (2.14)
(2.14)
Если ![]() - концентрация молекул А вдали от частицы, а
- концентрация молекул А вдали от частицы, а ![]() - концентрация паровой фазы на поверхности частицы, и частица первоначально находится в атмосфере частиц А с концентрацией, равной
- концентрация паровой фазы на поверхности частицы, и частица первоначально находится в атмосфере частиц А с концентрацией, равной ![]() , начальные, и граничные условия для (11.4) записываются так:
, начальные, и граничные условия для (11.4) записываются так:
![]() (2.15)
(2.15)
![]() (2.16)
(2.16)
![]() (2.17)
(2.17)
решение (2.14) в граничных условиях (2.5) - (2.17), будет выглядеть так:
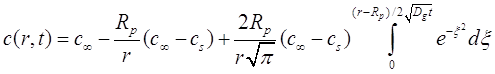 (2.18)
(2.18)
Временная зависимость концентрации в любом радиальном положении r дается третьим членом на правой стороне (2.18). Отметим, что для больших значений t, значение верхнего предела интегрирования приближается к нулю и профиль концентрации приближается к установившемуся состоянию, задаваемому
 (2.19)
(2.19)
Полный поток молекул А (молей в секунду) к частице обозначен Jc, индекс c показывает, что режим непрерывный (continuum), и задаётся, как:
![]() (2.20)
(2.20)
или, используя (2.19) и (2.13), как
![]() (2.21)
(2.21)
Если ![]() , поток молекул A - к частице, а если
, поток молекул A - к частице, а если ![]() - наоборот. Вышеупомянутый результат был впервые получен Максвеллом (1877), и (11.11) часто называется потоком Максвела.
- наоборот. Вышеупомянутый результат был впервые получен Максвеллом (1877), и (11.11) часто называется потоком Максвела.
Массовый баланс на растущей или испаряющейся частице:
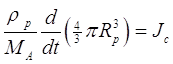 (2.22)
(2.22)
где ![]() - плотность частицы и
- плотность частицы и ![]() молекулярный вес A. Объединяя (2.21) с (2.22) получим,
молекулярный вес A. Объединяя (2.21) с (2.22) получим,
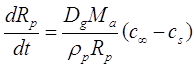 (2.23)
(2.23)
Когда ![]() и
и ![]() постоянны, (2.23) можно проинтегрировать, что даст:
постоянны, (2.23) можно проинтегрировать, что даст:
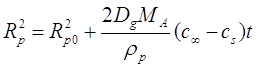 (2.24)
(2.24)
Использование независимого от времени установившегося профиля, заданного (2.19), для вычисления размера частицы во времени (11.24) может казаться противоречивым. Использование установившегося диффузионного потока, для вычисления темпа роста частицы подразумевает, что профиль концентрации пара около частицы достигает установившейся величины прежде, чем произойдёт заметное изменение величины молекулы. Так как рост действительно происходит в сотни раз медленнее чем диффузия, профиль около частицы фактически всегда остается в ее стационарном значении.
2.1.3 Свободно - молекулярный (кинетический) режим.В трёхмерном случае число столкновений молекул с единицей поверхности в единицу времени равно ![]() (Moore, 1962)
(Moore, 1962)
![]() , (2.25)
, (2.25)
где ![]() - скорость молекул:
- скорость молекул:
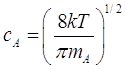 . (2.26)
. (2.26)
Учитывая это, молярный поток ![]() (молей в единицу времени) на частицу радиусом
(молей в единицу времени) на частицу радиусом ![]() :
:
![]() (2.27)
(2.27)
где ![]() - вероятность прилипания. Отношение молекулярного потока в кинетическом режиме к потоку в непрерывном режиме, равно:
- вероятность прилипания. Отношение молекулярного потока в кинетическом режиме к потоку в непрерывном режиме, равно:
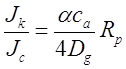 (2.28)
(2.28)
Установившийся поток молекул пара к сфере, когда частица является достаточно большой по сравнению со средней длинной свободного пробега молекул пара, задаётся уравнением Максвелла (2.20). Так как это уравнение основано на решении уравнения переноса в непрерывном режиме, оно перестаёт действовать, когда средняя длина свободного пробега молекул пара становится сопоставимым диаметру частицы. В другом случае, выражение, основанное на кинетической теории газов (2.27) также не справедливо в этом случае, где ![]() . Когда
. Когда ![]() , явления, как говорят, лежат в переходном режиме.
, явления, как говорят, лежат в переходном режиме.
Распределение концентрации диффузионных молекул и фонового газа в переходном режиме строго описывается уравнением Больцмана. К сожалению, не существует общего решения уравнения Больцмана, справедливого для всего диапазона чисел Кнудсена. Как следствие, большинство исследований явлений переноса избегает решать непосредственно уравнение Больцмана и ограничивают себя подходом, основанным на так называемом методе подгонки потоков. Подгонка потоков предполагает, что кинетические эффекты ограничены областью ![]() , а вне этой области имеет место непрерывный режим.
, а вне этой области имеет место непрерывный режим.
Расстояние ![]() имеет порядок средней длины свободного пробега
имеет порядок средней длины свободного пробега ![]() . Предполагают, что в пределах этой внутренней области применима простая кинетическая теория газов.
. Предполагают, что в пределах этой внутренней области применима простая кинетическая теория газов.
• Теория Фукса Соответствие непрерывных и свободномолекулярных потоков молекулы относится ко времени Николая Альбертовича Фукса, который предложил, что подгонкой двух потоков в ![]() , можно получить граничное условие к уравнению диффузии. Предположим, коэффициент прилипания равен единице,
, можно получить граничное условие к уравнению диффузии. Предположим, коэффициент прилипания равен единице,
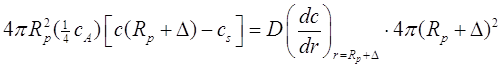 (2.29)
(2.29)
Тогда решая стационарное уравнение переноса для разбавленной системы,
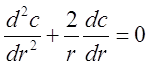 (2.30)
(2.30)
используя как граничные условия (11.27) и ![]() , получаем решение:
, получаем решение:
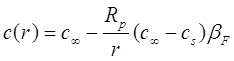 (2.31)
(2.31)
где поправочный коэффициент ![]() :
:
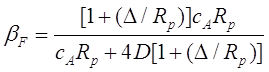 (2.32)
(2.32)
Связав бинарную диффузию и среднюю длину свободного пробега, используя ![]() , и
, и ![]() , получим:
, получим:
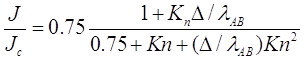 (2.33)
(2.33)
Заметим, что определение средней длины свободного пробега ![]() подразумевает, что для a= 1,
подразумевает, что для a= 1,
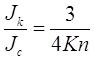 (2.34)
(2.34)
и отношение Фукса (2.33) преобразуется, используя (2.34),
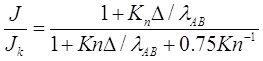 (2.35)
(2.35)
Значение ![]() , используемого в выражениях выше не было определено в теории и должно быть выбрано опытным путем или оценено в соответствии с независимой теорией. Несколько выборов для
, используемого в выражениях выше не было определено в теории и должно быть выбрано опытным путем или оценено в соответствии с независимой теорией. Несколько выборов для ![]() были предложены: самое простое, самим Фуксом,
были предложены: самое простое, самим Фуксом, ![]() =0. Другие предложения по этой теме высказаны Дэвисом , в 1983 году:
=0. Другие предложения по этой теме высказаны Дэвисом , в 1983 году: ![]() ,
, ![]() .
.
• Подход Фукса и Сутугина. Фукс и Сутугин в 1971 году последовали решению уравнения Больцмана, данного Сахни в 1966 году, для ![]() , где
, где ![]() - отношение молекулярного веса диффундирующего вещества и воздуха, для создания следующей интерполяционной формулы переходного режима.
- отношение молекулярного веса диффундирующего вещества и воздуха, для создания следующей интерполяционной формулы переходного режима.
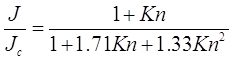 (2.36)
(2.36)
Уравнение (2.36) основано на результатах для ![]() и поэтому непосредственно применимо, чтобы описать молекулы в более тяжелом фоновом газе. Средняя длина свободного пробега, включенная в определение числа Кнудсена в (2.36):
и поэтому непосредственно применимо, чтобы описать молекулы в более тяжелом фоновом газе. Средняя длина свободного пробега, включенная в определение числа Кнудсена в (2.36): ![]() .
.
• Подход Дахнеке. Дахнеке(Dahneke) в 1983 использовал поток, соответствующий подходу Фукса, но, предполагая что - ![]() и
и ![]() , получил,
, получил,
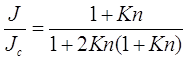 (2.37)
(2.37)
где ![]() . Средняя длина свободного пробега свободного пробега, включенного в определение числа Кнудсена в (2.37):
. Средняя длина свободного пробега свободного пробега, включенного в определение числа Кнудсена в (2.37): ![]()
• Подход Лоялки. Лоялка в 1983 построил улучшенные интерполяционные формулы для переходного режима, решая линеаризованное уравнения Больцмана с помощью БГК модели (Bhatnagar, Gross, Krook - 1954):
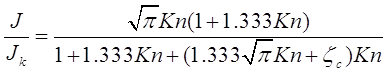 (2.38)
(2.38)
Средняя длина свободного пробега, используемая Лоялкой: ![]() , коэффициент скачка концентрации имел значение
, коэффициент скачка концентрации имел значение ![]() . Виллиамс и Лоялка в 1991 году указали, что (2.38) не работает вблизи свободно - молекулярного режима.
. Виллиамс и Лоялка в 1991 году указали, что (2.38) не работает вблизи свободно - молекулярного режима.
Для получения возможно более точных результатов по испарению и конденсации частиц применяются самые разные подходы: от полуэмпирических, некоторые из которых перечислены выше, до достаточно обоснованных с математической точки зрения. К этим работам, в частности, относится серия работ [16] - [21]. В основе этих работ лежит расчет потока пара на частицу интегрированием функции распределения, полученной в результате решения линеаризованного уравнения Больцмана:
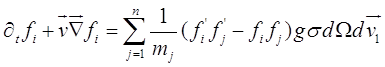 (2.39)
(2.39)
здесь: ![]() - одночастичная функция распределения по скоростям и координатам i-ого газового компонента,
- одночастичная функция распределения по скоростям и координатам i-ого газового компонента, ![]() - телесный угол,
- телесный угол, ![]() - вектор относительной скорости,
- вектор относительной скорости, ![]() - сечение столкновений,
- сечение столкновений, ![]() - скорость молекулы, которая сталкивается с рассматриваемой молекулой - для которой записывается уравнение Больцмана, суммирование производится по всем газовым составляющим. Вообще говоря, в левой части уравнения (2.39) следует добавить слагаемое -
- скорость молекулы, которая сталкивается с рассматриваемой молекулой - для которой записывается уравнение Больцмана, суммирование производится по всем газовым составляющим. Вообще говоря, в левой части уравнения (2.39) следует добавить слагаемое - ![]() , где
, где ![]() сила, действующая на молекулу, m - ее масса,
сила, действующая на молекулу, m - ее масса, ![]() - ее ускорение. Предполагается, что силовое поле отсутствует. В таком виде уравнение Больцмана слишком сложное, чтобы для него можно было найти решение, кроме самых простых случаев, например, для равновесного распределения по скоростям. В таком виде оно используется для исследования ее решений. Правая часть этого уравнения называется интегралом столкновения, вся сложность поиска решений связана именно с этим интегралом столкновений. В частности существует принцип Гильберта [26], [27], в соответствии с которым решение уравнения (2.39) можно найти в виде разложения по моментам распределения в начальный момент времени. На этом основан метод моментов Греда. Однако этот метод более применим к задачам гидродинамики, нежели, к проблемам кинетики. Основные приближения, которые используются для получения решения уравнения (2.39) сводятся к тому, чтобы упростить интеграл столкновений. При этом предполагается, что распределение по скоростям мало отличается от равновесного распределения. Таким образом конструируется уравнение для функции, описывающей отклонение распределения от равновесного. Этот подход аналогичен методам, описанным в работе Черчиньяни [21], [22]. В конечном счёте этот метод приводит к интегральному уравнению Фредгольма первого или второго рода - в зависимости от выбранной формы аппроксимации. Дополнительные осложнения возникают при постановке граничных условий. Наибольшие продвижения возможны в этом направлении при сферической форме испаряющихся капель. Попытки получить точное решение приводят к довольно сложным зависимостям, с которыми сложно работать и сопоставлять с экспериментальными данными. Кроме этого, приходится делать предположение скачка концентраций на поверхности частицы. Для диффузионного и около диффузионного режима столкновений молекул пара с частицей, когда задачу можно свести к решению уравнения диффузии, авторам [17] удалось создать метод расчета конденсации и испарения для несферических частиц, используя формализм функций Грина - задача сводится к решению соответствующего интегрального уравнения, при этом могут быть использованы численные методы - аналитические зависимости в этом случае получить не удается. Еще сложнее описать процессы испарения и конденсации частиц, в среде, состоящей из нескольких летучих компонентов [23]. Предполагалось, что процесс стационарный, испаряющиеся компоненты химически инертны, пары представляют собой идеальный газ. Для переходного режима использовалась формула Фукса - Сутугина. По сути, этот подход представлял собой применение ранее разработанных моделей для бинарной смеси. Сопоставление модельных расчетов с экспериментальными результатами испарения смеси азотной кислоты с водой показало, что при различных внешних условиях (соотношениях компонент и относительной влажности) большинство моделей можно применять, если подогнать соответствующим образом модельные параметры, например, вероятность прилипания.
- ее ускорение. Предполагается, что силовое поле отсутствует. В таком виде уравнение Больцмана слишком сложное, чтобы для него можно было найти решение, кроме самых простых случаев, например, для равновесного распределения по скоростям. В таком виде оно используется для исследования ее решений. Правая часть этого уравнения называется интегралом столкновения, вся сложность поиска решений связана именно с этим интегралом столкновений. В частности существует принцип Гильберта [26], [27], в соответствии с которым решение уравнения (2.39) можно найти в виде разложения по моментам распределения в начальный момент времени. На этом основан метод моментов Греда. Однако этот метод более применим к задачам гидродинамики, нежели, к проблемам кинетики. Основные приближения, которые используются для получения решения уравнения (2.39) сводятся к тому, чтобы упростить интеграл столкновений. При этом предполагается, что распределение по скоростям мало отличается от равновесного распределения. Таким образом конструируется уравнение для функции, описывающей отклонение распределения от равновесного. Этот подход аналогичен методам, описанным в работе Черчиньяни [21], [22]. В конечном счёте этот метод приводит к интегральному уравнению Фредгольма первого или второго рода - в зависимости от выбранной формы аппроксимации. Дополнительные осложнения возникают при постановке граничных условий. Наибольшие продвижения возможны в этом направлении при сферической форме испаряющихся капель. Попытки получить точное решение приводят к довольно сложным зависимостям, с которыми сложно работать и сопоставлять с экспериментальными данными. Кроме этого, приходится делать предположение скачка концентраций на поверхности частицы. Для диффузионного и около диффузионного режима столкновений молекул пара с частицей, когда задачу можно свести к решению уравнения диффузии, авторам [17] удалось создать метод расчета конденсации и испарения для несферических частиц, используя формализм функций Грина - задача сводится к решению соответствующего интегрального уравнения, при этом могут быть использованы численные методы - аналитические зависимости в этом случае получить не удается. Еще сложнее описать процессы испарения и конденсации частиц, в среде, состоящей из нескольких летучих компонентов [23]. Предполагалось, что процесс стационарный, испаряющиеся компоненты химически инертны, пары представляют собой идеальный газ. Для переходного режима использовалась формула Фукса - Сутугина. По сути, этот подход представлял собой применение ранее разработанных моделей для бинарной смеси. Сопоставление модельных расчетов с экспериментальными результатами испарения смеси азотной кислоты с водой показало, что при различных внешних условиях (соотношениях компонент и относительной влажности) большинство моделей можно применять, если подогнать соответствующим образом модельные параметры, например, вероятность прилипания.
С точки зрения корректности постановки задачи и нахождения ее решения следует отметить работу Сахни [24]. Вообще говоря, эта работа относится к расчету потока нейтронов - в замедлителе реактора с учетом поглощения их черными сферами. Тем не менее, она полностью применима для испарения и конденсации частиц сферической формы. По сути дела эта работа - решение задачи Милна для сферической геометрии. Эта задача была сведена к интегральному уравнению первого рода, затем преобразовано к сингулярному уравнению типа Коши, которое было затем решено численными методами. Эти результаты, в частности, были использованы Фуксом и Сутугиным [8] для получения аппроксимационной формулы переходного режима. Очевидно, что для получения точных соотношений для потока молекул на поверхность частицы, необходимо решать уравнение для функции распределения Больцмана. Все определяется тем, в каком виде брать правую часть этого уравнения, ниже мы вернемся к этому.
2.2 Постановка задачи.Наука об аэрозольных частицах началась c решения проблемы испарения в газообразной среде.
Предположим, нам известен радиус частицы – a, и концентрация молекул пара вокруг этой частицы – n(r), где r – радиус-вектор, построенный из точки начала координат (центр частицы). Требуется найти зависимость радиуса частицы от времени – a(t). Итак, массу частицы можно выразить как ![]() , где ρ – плотность частицы, площадь поверхности частицы -
, где ρ – плотность частицы, площадь поверхности частицы - ![]() , тогда будет справедливо уравнение:
, тогда будет справедливо уравнение:
 , (2.39)
, (2.39)
где j – плотность потока конденсирующихся молекул пара, m0 – масса молекулы. Продифференцировав левую часть и упростив уравнение (2.39) получим:
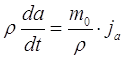 (2.40)
(2.40)
Проинтегрировав это выражение, получим:
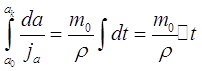 (2.41)
(2.41)
Видно, что для расчета скорости испарения или конденсации, что и составляет нашу задачу, необходимо знать величину потока молекул пара на поверхность частицы. Впервые ее записал Максвелл в конце 19-го века:
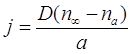 (2.42)
(2.42)
здесь j - это плотность потока конденсирующихся молекул пара (количество молекул осаждающихся на единице площади частиц в единицу времени); D - коэффициент диффузии молекул пара в газе-носителе, ![]() - концентрация пара на далеких от частицы расстояниях и у поверхности частицы соответственно; а - радиус частицы. Этот результат и его модификации справедливы для сравнительно крупных частиц, размер которых существенно превышает длину свободного пробега конденсирующихся молекул.
- концентрация пара на далеких от частицы расстояниях и у поверхности частицы соответственно; а - радиус частицы. Этот результат и его модификации справедливы для сравнительно крупных частиц, размер которых существенно превышает длину свободного пробега конденсирующихся молекул.
Другой предельный случай был получен значительно позже для свободно молекулярного режима: конденсационный поток пропорционален произведению тепловой скорости молекул ![]() и поперечному сечению частицы (квадрату радиуса частицы)
и поперечному сечению частицы (квадрату радиуса частицы)
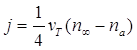 (2.43)
(2.43)
Как уже отмечалось выше, для переходного режима, когда уравнение для потока молекул преобразуется из вида (33) к форме (34), предложено довольно много подходов [2] - [11]. Из этих формул можно выделить выражение, предложенное Фуксом и Сутугиным, поскольку оно наиболее часто цитируется:
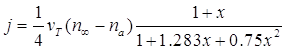 , (2.44)
, (2.44)
где х = а/l и l относительная и размерная длина свободного пробега. Если ввести термин - эффективность конденсации а - то задача будет сведена к нахождению этой величины, через которую определяется поток молекул на поверхность частицы:
![]() (2.45)
(2.45)
Таким образом, все усилия экспериментаторов и теоретиков сводились к определению именно этой величины.
Предлагаемый ниже подход основан на расчете эффективности конденсации а при помощи распределения молекул пара по скоростям и координатам, как это было сделано у Сахни [24]. Для получения этой функции распределения необходимо решать уравнение Больцмана. Чтобы упростить получение этого решения, правая часть уравнения Больцмана - интеграл столкновения - был линеаризован. Такой прием был предпринят Бхатнагаром, Гроссом и Круком [27] - так называемое БГК приближение. В этом БГК приближении используются наиболее простые граничные условия. Предполагается, что частично молекулы испытывают зеркальное отражение, а некоторые из молекул осаждаются на поверхности. В этом приближении интеграл столкновений представлен в довольно простом виде:
![]() (2.46)
(2.46)
здесь ![]() - не зависящая от скорости частота столкновений, эта величина имеет порядок
- не зависящая от скорости частота столкновений, эта величина имеет порядок ![]() , где а - радиус частицы, n - концентрация молекул пара, < v > - средняя скорость относительного движения молекул. Несмотря на то, что складывается впечатление, что сделано довольно грубое приближение - сложный интеграл столкновений заменен довольно простым слагаемым - в такой форме уравнение Больцмана сохраняет основные свои свойства, и, как будет видно ниже, эта простота кажущаяся. Можно легко показать, что решение уравнения (2.46)
, где а - радиус частицы, n - концентрация молекул пара, < v > - средняя скорость относительного движения молекул. Несмотря на то, что складывается впечатление, что сделано довольно грубое приближение - сложный интеграл столкновений заменен довольно простым слагаемым - в такой форме уравнение Больцмана сохраняет основные свои свойства, и, как будет видно ниже, эта простота кажущаяся. Можно легко показать, что решение уравнения (2.46)
· удовлетворяют уравнениям сохранения массы, импульса и энергии;
· удовлетворяет Н - теореме.
Простота уравнения (2.46) обманчива. Это уравнение имеет сильную нелинейность, таким образом, локальные параметры - масса, импульс и энергия должны определяться через одночастичную функцию распределения ![]() , поэтому, как будет видно ниже, в то время как удалось уйти от одних проблем, возникли другие. При построении приближений следует принимать во внимание, что вид уравнения (2.46) дает два характерных времени -
, поэтому, как будет видно ниже, в то время как удалось уйти от одних проблем, возникли другие. При построении приближений следует принимать во внимание, что вид уравнения (2.46) дает два характерных времени - ![]() - характерное время микроскопической релаксации, время за которое
- характерное время микроскопической релаксации, время за которое ![]() заметно меняется. Кроме этого, из-за наличия
заметно меняется. Кроме этого, из-за наличия ![]() возникает второе характерное время -
возникает второе характерное время -![]() . Легко показать, что
. Легко показать, что 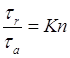 . Полученный конденсационный поток выражен через пространственную концентрацию конденсирующегося пара. Показано, что минимальной информации о профиле концентрации достаточно для получения точного аналитического выражения для молекулярного потока при произвольном режиме конденсации и произвольной вероятности прилипания. Это и есть основной результат предложенного подхода. Следует несколько слов сказать о соотношении между равновесной концентрацией пара и концентрацией пара у поверхности частицы. Вообще говоря, предполагается, что
. Полученный конденсационный поток выражен через пространственную концентрацию конденсирующегося пара. Показано, что минимальной информации о профиле концентрации достаточно для получения точного аналитического выражения для молекулярного потока при произвольном режиме конденсации и произвольной вероятности прилипания. Это и есть основной результат предложенного подхода. Следует несколько слов сказать о соотношении между равновесной концентрацией пара и концентрацией пара у поверхности частицы. Вообще говоря, предполагается, что ![]() , где
, где ![]() - равновесная концентрация пара вблизи поверхности частицы. В то же время это не совсем так. Например, при неединичной вероятности прилипания (β), концентрация вблизи поверхности частицы отличается от
- равновесная концентрация пара вблизи поверхности частицы. В то же время это не совсем так. Например, при неединичной вероятности прилипания (β), концентрация вблизи поверхности частицы отличается от ![]() и определяется кинетикой процесса переноса массы к частице. То же самое относится к переходному режиму конденсации, где скачок концентрации (также возникающий благодаря динамике переноса массы) заставляет поверхностную концентрацию отличаться от хорошо известного значения
и определяется кинетикой процесса переноса массы к частице. То же самое относится к переходному режиму конденсации, где скачок концентрации (также возникающий благодаря динамике переноса массы) заставляет поверхностную концентрацию отличаться от хорошо известного значения ![]() . На самом деле концентрацию
. На самом деле концентрацию ![]() саму необходимо находить из решения динамики столкновения, что ограничивает применение соотношения
саму необходимо находить из решения динамики столкновения, что ограничивает применение соотношения ![]() . Более детально эта проблема будет обсуждаться в рамках ВГК модели наряду с проблемой скачка концентрации.
. Более детально эта проблема будет обсуждаться в рамках ВГК модели наряду с проблемой скачка концентрации.
3. Решение задачи и результаты исследования 3.1 Линеаризованное уравнение Больцмана для сферической геометрии в односкоростном приближении.
Рассмотрим получение левой части уравнения для функции распределения Больцмана - найдем выражение оператора ![]() . Для решения уравнения введем новую систему ортогональных координат
. Для решения уравнения введем новую систему ортогональных координат ![]() . Эта система координат очень похожа на сферическую систему координат -
. Эта система координат очень похожа на сферическую систему координат - ![]() .
.
Связь вводимой системы координат - она также ортогональна - с декартовой может быть представлена системой уравнений:
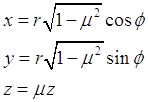 (3.1)
(3.1)
Для вычисления градиента в этой системе координат найдем метрический тензор:
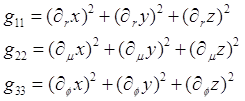 (3.2)
(3.2)
После простых вычислений можно получить:
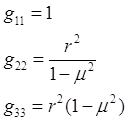 (3.3)
(3.3)
Тогда для градиента произвольной функции в этой системе координат:
![]() (3.4)
(3.4)
Где ![]() - соответствующие орты в направлениях
- соответствующие орты в направлениях ![]() . Тогда производная в направлении вектора
. Тогда производная в направлении вектора ![]() может быть представлена в форме:
может быть представлена в форме:
![]() (3.5)
(3.5)
Для рассматриваемой функции распределения Больцмана, как это было сделано в односкоростном приближении, соответствующим задаче Милна:
 (3.6)
(3.6)
Тогда левая часть уравнения для функции распределения Больцмана в системе координат, описанной ранее, будет выглядеть следующим образом:
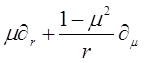 (3.7)
(3.7)
Предположим, что имеется сферическая частица (капля жидкости), которая окружена молекулами газа-носителя, концентрация которых ![]() - концентрации пара, который может как конденсироваться на капле, так и испаряться. Для того чтобы найти поток пара на частицу и распределение концентрации его вокруг частицы, необходимо рассчитать функцию распределения пара по координатам и ско5ростям. Для этого, вообще говоря, необходимо решить уравнение Больцмана. Будем считать, что линейная форма уравнения Больцмана дает хорошие результаты для рассматриваемого случая:
- концентрации пара, который может как конденсироваться на капле, так и испаряться. Для того чтобы найти поток пара на частицу и распределение концентрации его вокруг частицы, необходимо рассчитать функцию распределения пара по координатам и ско5ростям. Для этого, вообще говоря, необходимо решить уравнение Больцмана. Будем считать, что линейная форма уравнения Больцмана дает хорошие результаты для рассматриваемого случая:
![]()
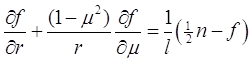 (3.8)
(3.8)
Здесь ![]() - функция распределения, зависящая от
- функция распределения, зависящая от ![]() и r, а r расстояние от центра частицы до r и
и r, а r расстояние от центра частицы до r и ![]() - угол между радиальным направлением и направлением скорости молекулы. Другие обозначения: l - средняя длина свободного пробега и
- угол между радиальным направлением и направлением скорости молекулы. Другие обозначения: l - средняя длина свободного пробега и
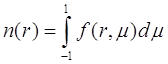 (3.9)
(3.9)
это численная концентрация молекул пара. Для простоты будем работать в системе единиц, где l = 1.
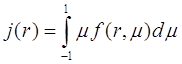 (3.10)
(3.10)
При интегрировании (3.8) по ![]() получается уравнение непрерывности:
получается уравнение непрерывности:
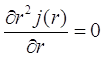 (3.11)
(3.11)
Функцию распределения удобно разбить на две части:
![]()
![]() (3.12)
(3.12)
где ![]() - единичная функция Хевисайда. С учетом (3.12) уравнение (3.8) дает два спаренных уравнения для
- единичная функция Хевисайда. С учетом (3.12) уравнение (3.8) дает два спаренных уравнения для ![]() и
и ![]() :
:
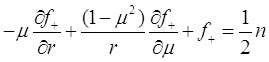 (3.13)
(3.13)
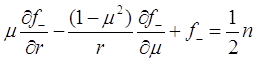 (3.14)
(3.14)
Функции ![]() и
и ![]() описывают молекулы пара двигающиеся по направлению к поверхности частицы и от частицы
описывают молекулы пара двигающиеся по направлению к поверхности частицы и от частицы ![]() . Численная концентрация молекул и их поток может быть выражен через эти функции:
. Численная концентрация молекул и их поток может быть выражен через эти функции:
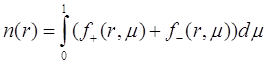 (3.15)
(3.15)
 (3.16)
(3.16)
Система уравнений (3.13) и (3.14) должна быть дополнена граничными условиями:
![]() (3.17)
(3.17)
Это наиболее простые граничные условия, устанавливающие связь между функциями ![]() и
и ![]() с помощью вероятности прилипания молекулы пара к поверхности частицы. Формула (3.9) означает, что доля налетающих на частицу молекул пара, которые остаются на ее поверхности, составляет
с помощью вероятности прилипания молекулы пара к поверхности частицы. Формула (3.9) означает, что доля налетающих на частицу молекул пара, которые остаются на ее поверхности, составляет ![]() , остальные молекулы, доля которых
, остальные молекулы, доля которых ![]() , зеркально отражаются от поверхности. Ниже будут представлены более общие граничные условия, которые не внесут существенных изменений в дальнейшее решение.
, зеркально отражаются от поверхности. Ниже будут представлены более общие граничные условия, которые не внесут существенных изменений в дальнейшее решение.
Введем новые переменные ![]() , которые связаны с
, которые связаны с ![]() соотношениями:
соотношениями:
![]() (3.18)
(3.18)
В этих переменных уравнения (3.6) и (3.7) принимают форму:
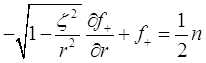 (3.19)
(3.19)
 (3.20)
(3.20)
Предположим, что ![]() - это известная функция координат, тогда решение уравнения (3.19) можно получить в виде:
- это известная функция координат, тогда решение уравнения (3.19) можно получить в виде:
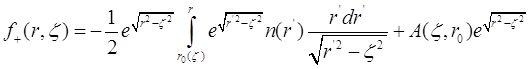 (3.21)
(3.21)
где ![]() . Правая часть уравнения (3.21) содержит растущую с r экспоненту, от которой следует избавиться выбором функции
. Правая часть уравнения (3.21) содержит растущую с r экспоненту, от которой следует избавиться выбором функции ![]() .Окончательный результат приобретает вид:
.Окончательный результат приобретает вид:
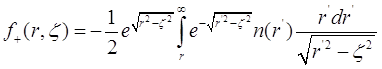 (3.22)
(3.22)
В переменных ![]() (3.22) имеют форму:
(3.22) имеют форму:
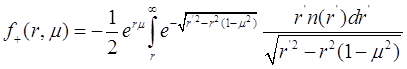 (3.23)
(3.23)
Теперь ![]() принимает вид:
принимает вид:
 (3.24)
(3.24)
Дальнейшие шаги связаны с получением явного вида решения (3.24). Для этого необходимо получить зависимость ![]() . Введем новую функцию
. Введем новую функцию ![]() уравнением:
уравнением:
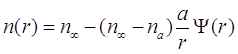 (3.25)
(3.25)
Эта функция предназначена для того, чтобы плавно перейти от значений концентрации пара на поверхности частицы к концентрации на далеких от частицы расстояниях. Естественно, ![]() . При подстановке выражения (3.24) в (3.25) получаем:
. При подстановке выражения (3.24) в (3.25) получаем:
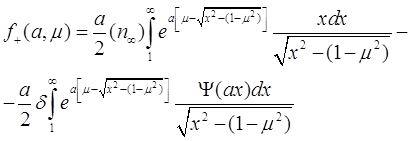 (3.26)
(3.26)
Здесь введены обозначения ![]() . Первый интеграл в правой части (3.26) легко посчитать:
. Первый интеграл в правой части (3.26) легко посчитать:
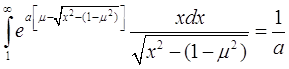 (3.27)
(3.27)
Второй тоже легко привести к удобному для использования виду, для этого введем замену переменных: ![]() ,
,  :
:
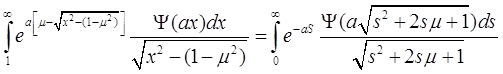 (3.28)
(3.28)
В результате для ![]() получим удобное выражение:
получим удобное выражение:
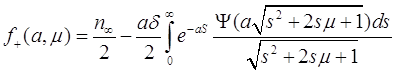 (3.29)
(3.29)
Теперь выражения для распределения концентрации ![]() и потока молекул j принимают форму:
и потока молекул j принимают форму:
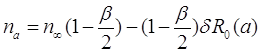 (3.30)
(3.30)
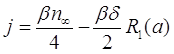 (3.31)
(3.31)
Здесь введены следующие обозначения ![]() и
и
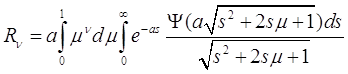 (3.32)
(3.32)
В соответствии с уравнением (3.11) можно записать, что ![]() , а также
, а также ![]() , откуда с учетом (3.25) при
, откуда с учетом (3.25) при ![]()
![]() для потока у поверхности частицы получим:
для потока у поверхности частицы получим:
 (3.33)
(3.33)
где D коэффициент диффузии (D=1/3 в БГК приближении) и введем обозначение ![]() . Таким образом, найдена связь между потоком у поверхности частицы с параметрами распределения концентрации пара на далеком удалении от нее.
. Таким образом, найдена связь между потоком у поверхности частицы с параметрами распределения концентрации пара на далеком удалении от нее.
Чтобы установить форму этой зависимости, ![]() представим в виде двух слагаемых, каждое из которых определяет поведение концентрации у поверхности и вдали от частицы:
представим в виде двух слагаемых, каждое из которых определяет поведение концентрации у поверхности и вдали от частицы:
![]()
![]() (3.34)
(3.34)
Здесь функция ![]() равна единице при
равна единице при ![]() и ничтожно мала на расстояниях порядка длины свободного пробега молекул пара и более (r порядка 1 в наших единицах). Тогда
и ничтожно мала на расстояниях порядка длины свободного пробега молекул пара и более (r порядка 1 в наших единицах). Тогда
![]() , (3.35)
, (3.35)
где
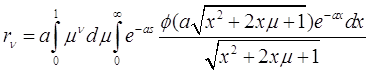 (3.36)
(3.36)
и
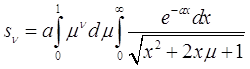 (3.37)
(3.37)
При подстановке соотношения (3.34) в уравнения (3.30) и (3.31) можно получить:
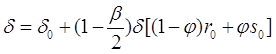 (3.38)
(3.38)
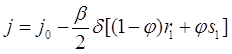 (3.39)
(3.39)
где![]() . Уравнение (3.33) позволяет исключить комбинацию
. Уравнение (3.33) позволяет исключить комбинацию ![]() при помощи линейной системы уравнений для
при помощи линейной системы уравнений для ![]() и
и ![]() :
:
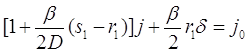 (3.40)
(3.40)
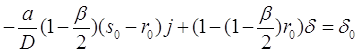 (3.41)
(3.41)
Решение этих уравнений можно представить через детерминанты:
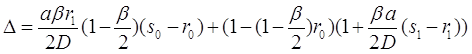 (3.42)
(3.42)
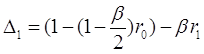 (3.43)
(3.43)
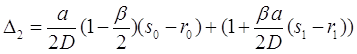 (3.44)
(3.44)
Окончательно получим:
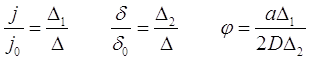 (3.45)
(3.45)
Можно получить и явную форму этих выражений:
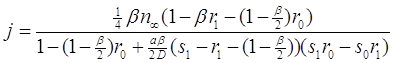 (3.46)
(3.46)
Следует учитывать, что, несмотря на то, что все выше полученные выражения точные, пока нет рецепта, как считать интегралы, входящие в выражения (3.42- 3.44). Для этого надо понять, как выбрать конкретный вид функции ![]() . Вообще говоря, это может быть сделано при нахождении точного решения уравнения (3.8). Однако на данном этапе это невозможно. На самом деле известны свойства функции
. Вообще говоря, это может быть сделано при нахождении точного решения уравнения (3.8). Однако на данном этапе это невозможно. На самом деле известны свойства функции ![]() , поэтому ее можно подобрать, используя подгоночные параметры пробных функций. Для этого необходимо с помощью этой функции суметь подобрать правильный профиль концентрации паров вокруг частицы. Такой функцией может быть зависимость вида:
, поэтому ее можно подобрать, используя подгоночные параметры пробных функций. Для этого необходимо с помощью этой функции суметь подобрать правильный профиль концентрации паров вокруг частицы. Такой функцией может быть зависимость вида:
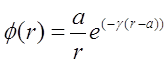 (3.47)
(3.47)
где величина параметра ![]() - это характерное расстояние, на котором свободно молекулярный режим переходит в непрерывный. Множитель
- это характерное расстояние, на котором свободно молекулярный режим переходит в непрерывный. Множитель ![]() - описывает профиль концентрации конденсирующихся паров в безстолкновительном режиме, когда поток пропорционален плотности, а не ее градиенту. Поскольку поток пропорционален
- описывает профиль концентрации конденсирующихся паров в безстолкновительном режиме, когда поток пропорционален плотности, а не ее градиенту. Поскольку поток пропорционален ![]() , то
, то ![]() . Экспоненциальный множитель аппроксимирует переход от свободно молекулярного режима к непрерывному. Таким образом, вместо уравнения (3.36) получается:
. Экспоненциальный множитель аппроксимирует переход от свободно молекулярного режима к непрерывному. Таким образом, вместо уравнения (3.36) получается:
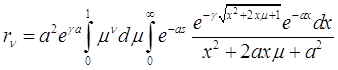 (3.48)
(3.48)
Представленная интерпретация достаточно прямолинейна, чувствительность окончательного результата к величине ![]() будет позже исследована. На рисунке 1 показан профиль концентрации при различных значениях величины
будет позже исследована. На рисунке 1 показан профиль концентрации при различных значениях величины ![]() . Вообще говоря,
. Вообще говоря, ![]() может быть найдена при помощи вариационных расчетов.
может быть найдена при помощи вариационных расчетов.
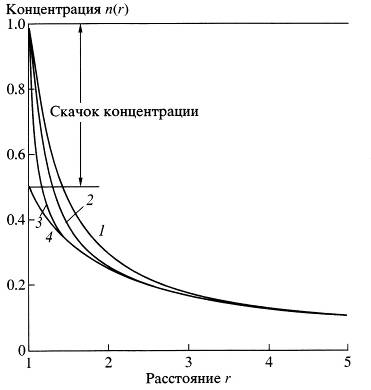
Рис. 1. Профиль концентрации вблизи поверхности частицы (см. уравнения (3.25), (3.34) и (3.47)). Концентрации нормированы на 1, расстояние измерено в длинах свободного пробега. Кривые 1-4 рассчитаны для ![]() = 1, 3, 10,
= 1, 3, 10, ![]() соответственно как функции расстояния от центра частицы. Радиус частицы а=1. Последняя кривая соответствует приближению скачка профиля концентрации: сам профиль концентрации получен из уравнения Фика, а граничные условия для концентрации пара - из решения кинетического уравнения (см. уравнение (3.59)).
соответственно как функции расстояния от центра частицы. Радиус частицы а=1. Последняя кривая соответствует приближению скачка профиля концентрации: сам профиль концентрации получен из уравнения Фика, а граничные условия для концентрации пара - из решения кинетического уравнения (см. уравнение (3.59)).
Итак, найдём параметр ![]() . Для этого построим функционал и минимизируем его численными методами с помощью ЭВМ. Итак, вспомним уравнение (3.13). Оно и станет основой для нашего функционала:
. Для этого построим функционал и минимизируем его численными методами с помощью ЭВМ. Итак, вспомним уравнение (3.13). Оно и станет основой для нашего функционала:
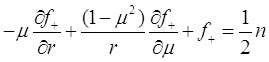 (3.49)
(3.49)
В результате преобразования получим:
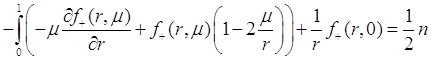 (3.50)
(3.50)
Теперь можно записать функционал, который надо минимизировать относительно параметра ![]() :
:
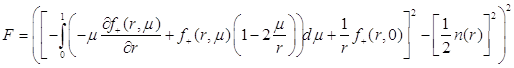 (3.51)
(3.51)
где
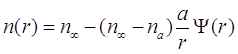 (3.52)
(3.52)
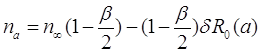 ,
, ![]() (3.53)
(3.53)
![]() ,
, ![]() (3.54)
(3.54)
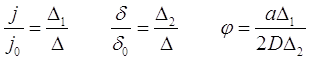 , (3.55)
, (3.55)
![]() (3.55)
(3.55)
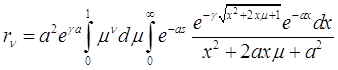 (3.56)
(3.56)
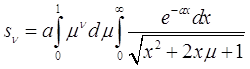 (3.57)
(3.57)
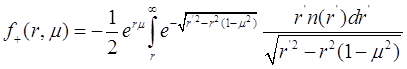 (3.58)
(3.58)
Вышеописанная модель была реализована в двух видах: в качестве программы на языке C с использованием библиотеки GSL, а так же в виде приложения пакета Mathcad. Рассмотрим полученные результаты:
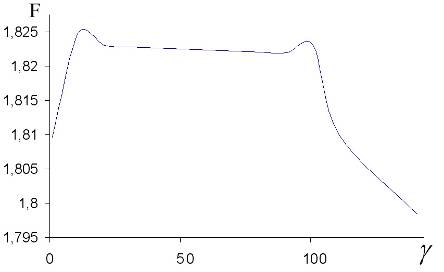
Рис. 2. Значение функционала (3.51) в диффузионном (непрерывном) режиме ![]() .
.
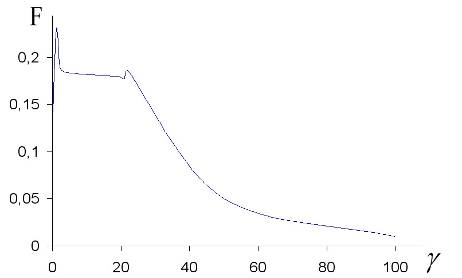
Рис. 3. Значение функционала (3.51) в переходном режиме ![]() .
.
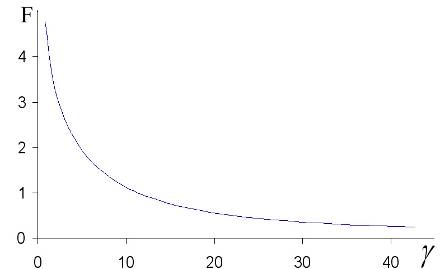
Рис. 4. Значение функционала (3.51) в свободномолекулярном (кинетическом) режиме ![]() .
.
Мы видим, что функционал уменьшается с ростом ![]() . Это соответствует скачку концентрации на поверхности частицы. Таким образом, модель оказалась чувствительной к скачку концентрации, то есть оправдывающей приближение, описанное ниже.
. Это соответствует скачку концентрации на поверхности частицы. Таким образом, модель оказалась чувствительной к скачку концентрации, то есть оправдывающей приближение, описанное ниже.
Рассмотрим влияние параметра на окончательный результат:
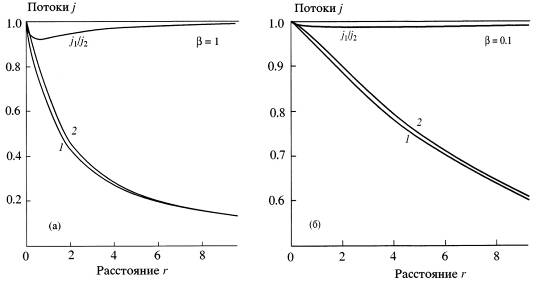
Рис. 5. Зависимость потока конденсирующихся паров ![]() . Потоки нормированы на 1, расстояния измерены в длинах свободного пробега: а) - полная вероятность прилипания, кривая 1 соответствует
. Потоки нормированы на 1, расстояния измерены в длинах свободного пробега: а) - полная вероятность прилипания, кривая 1 соответствует ![]() = 1, кривая 2 соответствует скачку концентрации (
= 1, кривая 2 соответствует скачку концентрации (![]() ), показано также и отношение этих потоков; б) - при уменьшении
), показано также и отношение этих потоков; б) - при уменьшении ![]() приближение скачка концентрации дает лучшую точность
приближение скачка концентрации дает лучшую точность
Из рисунка 5 видно, что окончательный результат не сильно зависит от параметра ![]() . Максимальное отклонение между граничными значениями
. Максимальное отклонение между граничными значениями ![]() и
и ![]() не превышает 10% и уменьшается при уменьшении
не превышает 10% и уменьшается при уменьшении ![]() .
.
Рассмотрим случай, когда ![]() . При больших
. При больших ![]() функция
функция ![]() ведет себя довольно резко (на расстояниях порядка
ведет себя довольно резко (на расстояниях порядка ![]() ), при этом она изменяется от
), при этом она изменяется от ![]() до
до ![]() (см. рис. 1). На предельном значении
(см. рис. 1). На предельном значении ![]() это изменение соответствует скачку концентрации между значениями
это изменение соответствует скачку концентрации между значениями ![]() и
и ![]() . Интегралы
. Интегралы ![]() находятся в этом пределе. Конечно, это приближение оставляет правильным асимптотическое поведение потока при больших и малых значениях а. Если пренебречь выражением, пропорциональным
находятся в этом пределе. Конечно, это приближение оставляет правильным асимптотическое поведение потока при больших и малых значениях а. Если пренебречь выражением, пропорциональным ![]() , то можно из уравнений (3.40) и (3.41) получить:
, то можно из уравнений (3.40) и (3.41) получить:
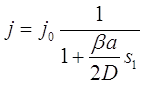 (3.59)
(3.59)
 (3.60)
(3.60)
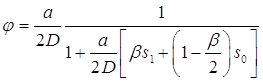 (3.61)
(3.61)
При выводе этих уравнений было использовано то, что ![]() .
.
Зависимости j от вероятности прилипания ![]() показаны на рисунке 6 для различных размеров частиц а.
показаны на рисунке 6 для различных размеров частиц а.
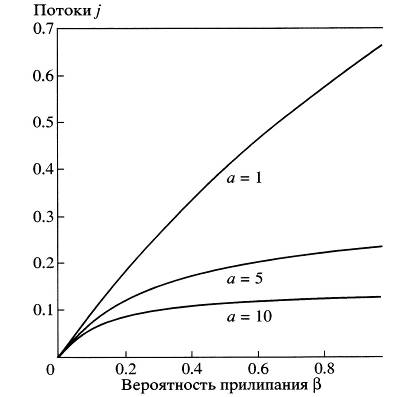
Рис. 6. Зависимость относительного потока конденсирующихся паров ( ![]() ,где
,где ![]() - поток при свободно молекулярном режиме при
- поток при свободно молекулярном режиме при ![]() ) от вероятности прилипания
) от вероятности прилипания ![]() . Расстояния измерены в длинах свободного пробега. При расчетах использовалась система уравнений (3.38).
. Расстояния измерены в длинах свободного пробега. При расчетах использовалась система уравнений (3.38).
Поток ![]() был найден из уравнения (3.59), а после этого был сопоставлен с формулой Фукса-Сутунгина, которая для произвольных
был найден из уравнения (3.59), а после этого был сопоставлен с формулой Фукса-Сутунгина, которая для произвольных ![]() может быть переписана в форме уравнения (3.59) с
может быть переписана в форме уравнения (3.59) с ![]() , замененным на
, замененным на ![]() ([10]):
([10]):
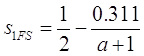 (3.62)
(3.62)
Соответствие между формулами, как можно видеть из рисунков 8 и 9, не требует комментариев за исключением того, что при малых ![]() это соответствие становится хуже.
это соответствие становится хуже.

Рис. 7. Поток конденсирующихся паров: сравнение приближения скачка концентрации с формулой Фукса-Сутугина при вероятности прилипания ![]() =1. Потоки вблизи поверхности частицы нормированы на 1, расстояния измерены в длинах свободного пробега. Кривая 1: формула Фукса-Сутугина. Кривая 2: приближение скачка концентрации (уравнение (3.59)).
=1. Потоки вблизи поверхности частицы нормированы на 1, расстояния измерены в длинах свободного пробега. Кривая 1: формула Фукса-Сутугина. Кривая 2: приближение скачка концентрации (уравнение (3.59)).
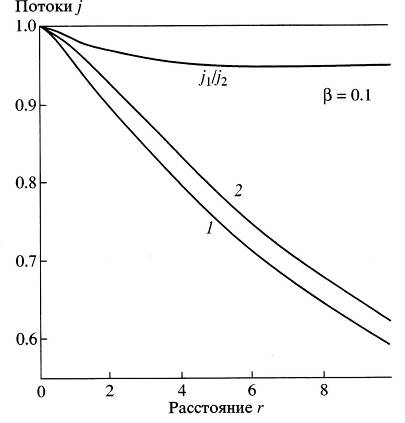
Рис. 8. Поток конденсирующихся паров: сравнение приближения скачка концентрации с формулой Фукса-Сутугина при вероятности прилипания ![]() = 0.1. Потоки вблизи поверхности частицы нормированы на 1, расстояния измерены в длинах свободного пробега. Кривая 1: формула Фукса-Сутугина. Кривая 2: приближение скачка концентрации (уравнение (3.59)).
= 0.1. Потоки вблизи поверхности частицы нормированы на 1, расстояния измерены в длинах свободного пробега. Кривая 1: формула Фукса-Сутугина. Кривая 2: приближение скачка концентрации (уравнение (3.59)).
График роста частицы для различных вероятностей прилипания представленная на рисунке 9 и рисунке 10 была найдена из уравнений (2.41) и (3.59).
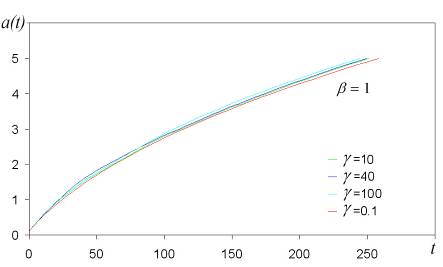
Рис. 9. Размер частицы a(t), найденный из уравнений (2.41) и (3.59). Масса и плотность налетающих частиц взяты равными единице.
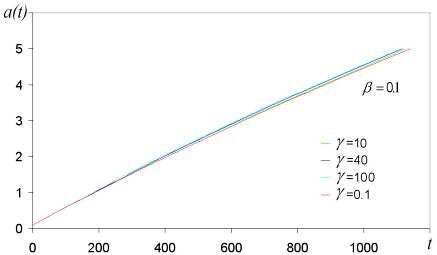
Рис. 10. Размер частицы a(t), найденный из уравнений (2.41) и (3.59). Масса и плотность налетающих частиц взяты равными единице.
4. Выводы и заключение.
В результате работы над дипломом было сделано:
1. Исследован процесс конденсации при различных числах Кнудсена.
2. Для расчета плотности потока молекул пара на частицу было использовано решение линеаризованного уравнения Больцмана.
3. Оценено значение параметра решения уравнения Больцмана для широкого диапазона значений чисел Кнудсена.
4. Выявлено, что модель односкоростного приближения дает скачок концентрации на поверхности. Это означает, что значение параметра решения должно быть очень большим.
5. Численные эксперименты показали, что наиболее важные величины, поток молекул пара, скорость роста частицы, слабо зависят от значения определяемого параметра.
6. При малых значениях вероятности прилипания эта зависимость становится еще меньше.
7. Предложен и реализован алгоритм расчета конденсационного роста частиц при различных числах Кнудсена вероятностях прилипания молекул пара к поверхности частицы.
Список литературы
1. J.C. Maxwell Collected Scientific Papers, Cambridge, 11, 625, 1890.
2. Фукс Н.А. Испарение и рост капель в газообразной среде. - Изд. АН СССР, Итоги науки, с. 90, 1958.
3. Н.Фукс, ЖЭТФ, т.4, вып. 7, 1934.
4. Li Y.Q., Davidovits P., Shi Q., Jayne J.T., Kolb C.E., Worsnop D.R. Mass and Thermal Accomodation Coefficients of H2O(g) on Liquid Water as Function of Temperatrue. - J.Phys.Chem.A, 105, 29, 10627-10634, 2001.
5. Heidenreich S., Buttner H. Investigation about the infuence of the Kelvin effect on droplet growth rate. - J.Aerosol Sci., v.26, n.2, 335 - 339, 1995.
6. Shi Q., Davidovits P., Jayne J.T., Worsnop D.R., Kolb C.E. Uptake of gas-phase ammonia. 1. Uptake by aqueous surfases as function of pH. - Mass and Thermal Accomodation Coefficients of H2O(g) on Liquid J.Phys.Chem.A, 103, 29, 8812-8823, 1999.
7. Swartz E., Shi Q., Davidovits P., Jayne J.T., Worsnop D.R., Kolb C.E. Uptake of gas-phase ammonia. 2. Uptake by sufuric acid surfaxres J.Phys.Chem.A, 103, 29, 8824-8833 1999
8. Widmann J.F., Davis E.J. Mathemetical models of the uptake of C1ONO2 and other gases by atmospheric aerosols. - J.AerosoI Sci., v.28, n.2, pp. 87 - 106, 1997.
9. Fuchs N.A., Sutugin A.G. Highly dispersed aerosols, in Topicsin Current Aerosol Research (Part 2), ed. by CM. Hidy and J.R. Brock, New York, pp. 1-200, 1971.
10. Dahneke B. Simple kinetic theory of Brownian diffusion in vapor and aerosols, in Theory of Dispersed Multiphase Flow, ed. by R.E. Meyer Academic Press, New York, pp. 97 - 133, 1983.
11. Loyalka S.K. Modelling of condensation in aerosols. - Prog. Nucl.Energy, v.12, pp.1-? 1983.
12. Sitarski M., Nowakowski B. Condensation rate of trace vapor on Knudsen aerosols from solution of the Boltzmann equation. - J.Colloid Interface Sci., v.72, pp.113-122, 1979.
13. Лушников А.А., Загайнов В.А. Кинетические эффекты конденсации при произвольной вероятности прилипания молекул к частицам. - Изв. АН, сер. ФАС), т.38, №2, с. 192 - 199.
14. К. Черчиньяни. Теория и приложения уравнения Больцмана. - Изд. Мир. Москва, 1978.
15. Резибуа П., Де Ленер П. Классическая кинетическая теория жидкостей и газов. - Изд. Мир, Москва, 1980.
16. Bhatnagar P.L., Gross E.P., Krook M. A model for collision processes in gases.
Похожие работы
... вскипающей жидкости от давления на входе при стационарном истечении. Сравнение расчетных данных с экспериментальными. Предполагается, что предлагаемый подход к моделированию стационарного и нестационарного истечения вскипающих жидкостей позволит получить полезную информацию и детализировать сопутствующие тепломассообменные и гидродинамические процессы. Обозначения d -диаметр канала; L - ...
... от используемого сырья, технологии синтеза и типа плазмотрона; их частицы являются монокристаллами и имеют размеры 10-100 нм и более. Процессы, происходящие при плазмохимическом синтезе и газофазном методе получения наночастиц, близки между собой. После взаимодействия в плазме происходит образование активных частиц, находящихся в газовой фазе. В дальнейшем необходимо сохранить их наноразмеры и ...
... натекатель плавно впускают атмосферный воздух. Выравнивание давлений внутри и вне колпака даёт возможность поднять его и начать следующий цикл обработки. Процесс термического вакуумного напыления характеризуется температурой на испарителе t°ис, давлением воздуха в рабочей камере P0, температурой нагрева подложек t°п. Температура нагрева вещества в испарителе (t°ис) должна обеспечивать достаточно ...
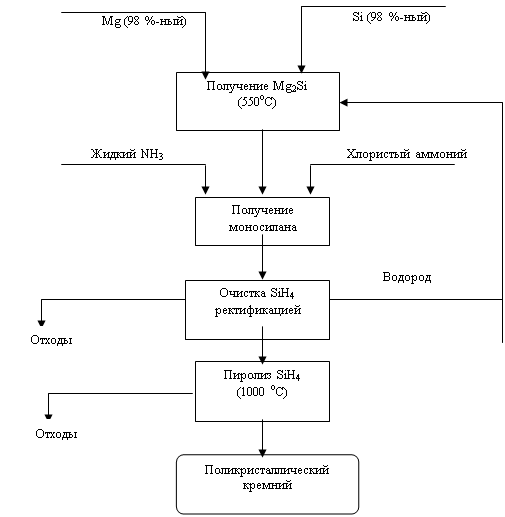
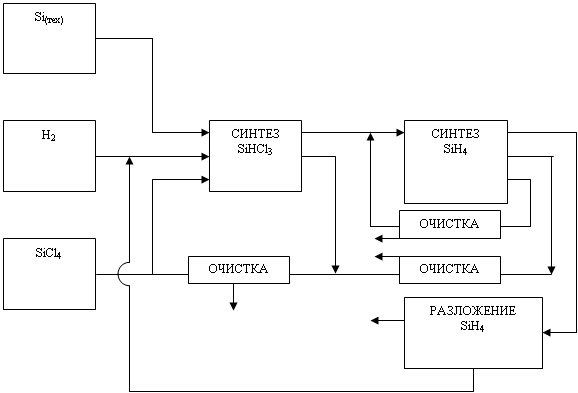
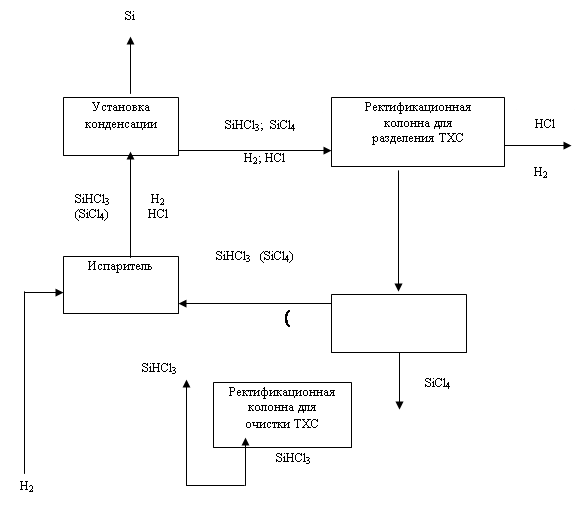
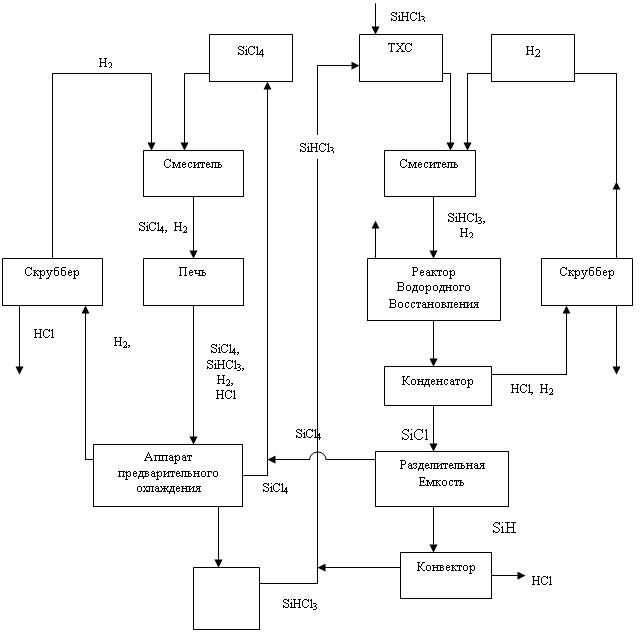
... опытно-промышленном масштабе кремния термическим разложением трибромсилана. Однако перспектива метода на сегодня остается неясной. В настоящее время основными химико-технологическими системами (ХТС), применяемыми всеми ведущими производителями кремния в мире являются производства, использующие трихлорсилан (78-90% всего производства кремния) и моносилан (18-20%). Разработки технологий на основе ...
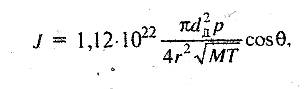

0 комментариев