Максимальные факторизации симплектических групп

Министерство образования Республики Беларусь

Учреждение образования

«Гомельский государственный университет им. Ф. Скорины»

Математический факультет

Дипломная работа

Максимальные факторизации симплектических групп

Исполнитель:

Студентка группы М-32

Макаренко Л.А.

Научный руководитель:

Канд. физ-мат. наук, доцент

Сафонов В.Г.

Гомель 2006

Оглавление

 

Введение

Перечень условных обозначений

Основные понятия

Изометрии

Проективные преобразования

Структурные теоремы. Порядки симплектических групп

Центры

Коммутанты

Теоремы о простоте

Основные результаты

Заключение

Список использованных источников

Введение

Говорят, что конечная группа  допускает факторизацию, если  для некоторых подгрупп  и  группы . При этом возникают две задачи: какие факторизации допускает заданная группа  и как строение сомножителей  и  влияет на строение самой группы . Естественно, что изучение конечных групп, обладающих факторизацией, дает возможность глубже понять строение конечной группы. Данная тематика изучалась такими видными математиками как Ф. Холл, С.А. Чунихин, Х. Виландт, Л.С. Казарин, Д.И. Зайцев, С.А. Сыскин и др. Ими был доказан ряд глубоких результатов в теории конечных групп. Аналогичные задачи возникают и в других разделах математики (например, в алгебрах Ли).

После завершения классификации конечных простых неабелевых групп актуальной стала задача получения факторизаций конкретных простых неабелевых групп и, в частности, простых групп лиевского типа малого лиевского ранга. Данные вопросы рассматривались Н. Ито, который получил все факторизации линейных групп лиевского ранга 1 над конечным полем Галуа, а также С. Блаумом, описавшим факторизации линейных и унитарных групп размерности 3.

В дипломной работе рассмотрены факторизации четырехмерных симплектических групп. Для таких групп найдены все максимальные факторизации.

Перечень условных обозначений

 

В работе все рассматриваемые группы предполагаются конечными. Буквами  обозначаются простые числа.

Будем различать знак включения множеств  и знак строгого включения ;

 и  - соответственно знаки пересечения и объединения множеств;

 - мощность множества ;

 - пустое множество;

 - множество всех простых чисел;

 - некоторое множество простых чисел, т.е. ;

 - дополнение к  во множестве всех простых чисел; в частности, ;

Пусть  - группа. Тогда:

 - порядок группы ;

 - порядок элемента  группы ;

 - единичный элемент и единичная подгруппа группы ;

 - множество всех простых делителей порядка группы ;

 - множество всех различных простых делителей натурального числа ;

-группа - группа , для которой ;

-группа - группа , для которой ;

 - подгруппа Фраттини группы , т.е. пересечение всех максимальных подгрупп ;

 - наибольшая нормальная разрешимая подгруппа группы ;

 - наибольшая нормальная --подгруппа группы ;

 - наибольшая нормальная --подгруппа группы ;

 - --холловская подгруппа группы ;

 - силовская --подгруппа группы ;

 - дополнение к силовской --подгруппе в группе , т.е. --холловская подгруппа группы ;

 -  является подгруппой группы ;

 -  является собственной подгруппой группы ;

 -  является максимальной подгруппой группы ;

 -  является нормальной подгруппой группы ;

 -  является минимальной нормальной подгруппой группы ;

 - индекс подгруппы  в группе ;

;

 - централизатор подгруппы  в группе ;

 - нормализатор подгруппы  в группе ;

 - центр группы ;

 - циклическая группа порядка ;

Если , то .

Если , , то .

Классы групп, т.е. совокупности групп, замкнутые относительно изоморфизмов, обозначаются прописными готическими буквами. За некоторыми классами закреплены стандартные обозначения:

 - класс всех сверхразрешимых групп;

 - класс всех разрешимых групп.

Основные понятия

Группой называется непустое множество  с бинарной алгебраической операцией (умножением), которая удовлетворяет следующим требованием:

1) операция определена на , т.е.  для всех ;

2) операция ассоциативна, т.е.  для любых ;

3) в  существует единичный элемент , т.е. такой элемент , что  для всех , что  для всех ;

4) каждый элемент обладает обратным, т.е. для любого  существует такой элемент , что .

Более кратко: полугруппа с единицей, в которой каждый элемент обладает обратным, называется группой.

Группу с коммутативной операцией называют коммутативной или абелевой. Если  - конечное множество, являющиеся группой, то  называют конечной группой, а число  элементов в  - порядком группы .

Подмножество  группы  называется подгруппой, если  - группа относительно той же операции, которая определена на . Запись  означает, что  - подгруппа группы , а  - что  - собственная подгруппа группы , т.е.  и .

Теорема  Непустое подмножество  группы  будет подгруппой тогда и только тогда, когда  и  для всех .

Пусть  - непустое подмножество группы . Совокупность всех элементов группы , перестановочных с каждым элементом множества , называется централизатором множества  в группе  и обозначается через .

Лемма  1. Если  - подмножество группы , то централизатор  является подгруппой.

2. Если  и  - подмножество группы  и , то .

3. Если  - подмножество группы  и , то .

Центром группы  называется совокупность всех элементов из , перестановочных с каждым элементом группы. Центр обозначается через . Ясно, что , т.е. центр группы  совпадает с централизатором подмножества  в группе . Кроме того, .

Зафиксируем в группе  элемент . Пересечение всех подгрупп группы , содержащих элемент , назовем циклической подгруппой, порожденной элементом , и обозначим через .

Теорема  Циклическая подгрупппа , порожденная элементом , состоит из всевозможных целых степеней элемента , т.е. .

Следствие  Циклическая подгруппа абелева.

Пусть  - элемент группы . Если все степени элемента  различны, т.е.  для всех целых , то говорят, что элемента  имеет бесконечный порядок.

Если  - непустое подмножество группы  и  то  и . Элемент  называется перестановочным с подмножеством , если . Равенство  означает, что для любого элемента  существует такой элемент , что . Если элемент  перестановочен с подмножеством , то  и . Совокупность всех элементов группы , перестановочных с подмножеством , называется нормализатором подмножества  в группе  и обозначается через . Итак,

Лемма Пусть  - непустое подмножество группы ,  - произвольный элемент группы . Тогда:

1) ;

2) ;

3) ;

4) ;

5) если  - подгруппа группы , то .

Подгруппа  называется нормальной подгруппой группы , если  для всех . Запись  читается: " - нормальная подгруппа группы ". Равенство  означает, что для любого элемента  существует элемент  такой, что .

Теорема  Для подгруппы  группы  следующие утверждения эквивалентны:

1) - нормальная подгруппа;

2) подгруппа  вместе с каждым своим элементом содержит все ему сопряженные элементы, т.е.  для всех ;

3) подгруппа  совпадает с каждой своей сопряженной подгруппой, т.е.  для всех .

Лемма  Пусть  - подгруппа группы . Тогда:

1) ;

2) если  и , то ;

3)  - наибольшая подгруппа группы , в которой  нормальна;

4) если , то . Обратно, если , то ;

5)  для любого непустого подмножества  группы .

В каждой группе  тривиальные подгруппы (единичная подгруппа  и сама группа ) являются нормальными подгруппами. Если в неединичной группе  нет других нормальных подгрупп, то группа  называется простой. Единичную группу  считают непростой.

Изометрии

Знакопеременные пространства

Векторное пространство  над полем  называется знакопеременным, если на нем задана знакопеременная билинейная форма , т. е. отображение  со следующими свойствами:

для всех , ,  из  и всех  из . Отметим следствие этих соотношений:

Если  - знакопеременная форма и  - произвольный элемент из , то отображение , определенное формулой , также знакопеременно, и сложный объект, являющийся исходным векторным пространством  с этой новой формой , будет знакопеременным пространством, которое мы обозначим через .

Представление знакопеременного пространства  в знакопеременное пространство  (оба над полем  и с формами, обозначаемыми через ) есть по определению линейное преобразование  пространства  в , такое, что  для всех , . Инъективное представление называется изометрией  в . Пространства  и  называются изометричными, если существует изометрия  на . Пусть  обозначает представление,  - изометрию ``в'', а  или  - изометрию ``на''. Очевидно, что композиция двух изометрии - изометрия и преобразование, обратное к изометрии, - также изометрия. В частности, множество изометрий пространства  на себя является подгруппой общей линейной группы  абстрактного векторного пространства ; она называется симплектической группой знакопеременного пространства  и обозначается через . Для любого ненулевого элемента  из  имеем .

Предложение  Пусть  - линейное преобразование знакопеременного пространства  в знакопеременное пространство . Предположим, что существует база  пространства , такая, что  для всех , . Тогда -- представление.

Доказательство. Это тривиально следует из определений.

Каждому знакопеременному пространству  со знакопеременной формой  сопоставим отображения  и  пространства  в сопряженное пространство  ( рассматривается как абстрактное векторное пространство над ). По определению отображение  сопоставляет произвольному элементу  из  линейный функционал , определенный формулой , а  переводит  в . Легко проверяется, что  и  являются линейными преобразованиями.

 - матрица  над  называется кососимметрической, если , и знакопеременной, если  и на главной диагонали стоят нули. Таким образом, знакопеременные матрицы являются кососимметрическими. Обратно, кососимметрические матрицы являются знакопеременными, если характеристика поля  не равна . Рассмотрим знакопеременное пространство . Мы можем ассоциировать с базой  пространства  матрицу, у которой на месте  стоит . Назовем  матрицей знакопеременного пространства  в базе  и будем писать

Если существует хотя бы одна база, в которой  имеет матрицу , то будем писать . Матрица , ассоциированная со знакопеременным пространством  указанным способом, является, очевидно, знакопеременной. Что происходит при изменении базы? Предположим, что  в базе  и  - матрица перехода от первой базы ко второй, т. е.

Тогда

откуда видно, что изменение матрицы пространства  при изменении базы описывается соотношением .

Если  - абстрактное векторное пространство с базой  и  - произвольная знакопеременная -матрица над , то существует единственный способ превратить  в знакопеременное пространство, такое, что  в , а именно, положить

где  - элемент, стоящий в матрице  на месте .

Предложение Предположим, что  - знакопеременное пространство,  - его база и  в . Тогда матричный изоморфизм, определенный базой , отображает  на группу всех обратимых -матриц  над , удовлетворяющих соотношению

Дискриминантом  векторов  в знакопеременном пространстве  называется определитель

В частности, если  - база пространства  и  в этой базе, то

Если  - другая база, то соотношение  показывает, что

для некоторого  из . Следовательно, канонический образ элемента  в  не зависит от базы; он называется дискриминантом знакопеременного пространства  и обозначается через . Здесь множество  определяется очевидным образом: берем факторгруппу , присоединяем к ней нуль 0 и полагаем, что произведение нуля и любого другого элемента равно нулю. Запись , где , будет обозначать, что  равно каноническому образу элемента  в  или, другими словами, что  обладает базой , для которой . Если , то полагаем .

Пример Рассмотрим знакопеременное пространство  со знакопеременной формой . Пусть  - его база, а  - сопряженная база сопряженного пространства . Пусть  в . Тогда . Легко видеть, что матрица линейного преобразования , определенного ранее, относительно баз  и  равна ; действительно, если , то

Аналогично матрица преобразования  относительно баз  и  равна .

Предложение  Любые  векторов  знакопеременного пространства , такие, что , линейно независимы.

Доказательство. Зависимость  влечет за собой  для . Это означает зависимость между строками матрицы , что невозможно, так как дискриминант не равен 0.

Предложение Следующие утверждения для знакопеременного пространства  равносильны:

 • ,

 • ,

 • ,

 •  биективно,

 •  биективно.

Доказательство. Можно считать, что . Зафиксируем базу  пространства , и пусть  - сопряженная база. Пусть  в . Ввиду (??)

 

	обратима
	биективно,

поэтому (3) равносильно (5). Аналогично (3) равносильно (4). Далее

биективно
	,

так что (5) равносильно (2). Наконец, очевидно, что (2) равносильно (1).

Определение Знакопеременное пространство  называется регулярным, если оно удовлетворяет одному из пяти равносильных условий (??). Знакопеременное пространство  называется вырожденным, если оно не является регулярным. Наконец, оно называется вполне вырожденным, если .

Если , то  регулярно. Если , то ввиду (??) и (??)

Предложение  Пусть  - представление знакопеременных пространств. Если  регулярно, то  - изометрия.

Доказательство. Возьмем  из ядра представления . Тогда . Отсюда ввиду регулярности пространства  получаем, что .

Предложение Каждой базе  регулярного знакопеременного пространства  соответствует единственная база  этого пространства, называемая сопряженной к  относительно  и такая, что  для всех , . Если  в  и  в , то .

Доказательство. 1) Положим  для , где  - сопряженная к  база сопряженного пространства . Тогда  - база, так как  биективно. Кроме того,

Этим доказано существование базы . Единственность непосредственно следует из регулярности.

2) Пусть . Тогда  и

Отсюда , так что  и .

Рассмотрим знакопеременное пространство  со знакопеременной формой . Будем говорить, что  имеет ортогональное разложение

на подпространства  если оно является прямой суммой  с попарно ортогональными , т. е.  при . Назовем  компонентами этого ортогонального разложения. Будем говорить, что подпространство  расщепляет  или что  является компонентой пространства , если существует подпространство  пространства , такое, что . Имеем

где произведение берется в .

Рассмотрим два знакопеременных пространства  и  над одним и тем же полем  и предположим, что имеется ортогональное разложение , а  - сумма пространств , , причем  при . Пусть для каждого , , задано представление . Тогда, как известно из линейной алгебры, существует единственное линейное преобразование , согласующееся с каждым  на . На самом деле легко проверить, что  - представление. Мы будем записывать его в виде

Важным является случай, когда ,  для всех  и  для всех ; тогда

Если дано еще одно такое представление , то

Рассмотрим знакопеременное пространство  над полем . Под ортогональным дополнением подпространства  пространства  в  понимается подпространство

совпадающее также с

Определим радикал пространства  как подпространство . Очевидно,

Предложение Пусть  - знакопеременное пространство, являющееся суммой попарно ортогональных подпространств, т. е. , где  при . Тогда

 • ,

 •  регулярно  каждое  регулярно,

 •  регулярно .

Доказательство. (1) Возьмем в  произвольный элемент  и запишем его в виде , . Тогда

так что , откуда . Обратно, если , где , то

откуда .

(2) Это следует из (1) и того, что знакопеременное пространство регулярно тогда и только тогда, когда его радикал равен .

(3) Если , , то

откуда . Следовательно,  и, значит, .

Предложение  Если  - подпространство знакопеременного пространства , то  - аннулятор пространства  в , т. е. . В частности, .

Доказательство непосредственно следует из определений.

Предложение  Пусть  - регулярное подпространство знакопеременного пространства . Тогда  расщепляет , точнее, . Если  - другое расщепление, .

Доказательство. Так как  регулярно, то . Следовательно, ввиду (??)

Поэтому  и, значит, . Далее, если , то , откуда . Сравнивая размерности, получаем .

Предложение  Если  и  - произвольные подпространства регулярного знакопеременного пространства  размерности , то

 • ,

 • ,

 • ,

 • ,

 • .

Доказательство. Так как  регулярно, то ввиду (??) отображение  биективно. Следовательно, , откуда ввиду (??) . Этим доказано (1). Далее, , поэтому сравнение размерностей дает . Этим доказано (2). Докажем теперь (3):

Аналогично доказывается (4). Наконец, утверждение (5) тривиально.

Рассмотрим радикал  знакопеременного пространства , и пусть  - подпространство пространства , такое, что . Назовем всякое такое разложение радикальным разложением пространства . Очевидно,  определяется не единственным образом, за исключением случаев, когда  регулярно или вполне вырождено. Из соотношений

следует равенство , поэтому  регулярно.

Теорема  Если  - регулярное знакопеременное пространство размерности , то

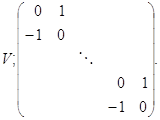
В частности, регулярное знакопеременное пространство имеет четную размерность и дискриминант . Кроме того, регулярные знакопеременные пространства одинаковой размерности над одним и тем же полем  изометричны.

Доказательство. Ввиду регулярности пространства  существуют векторы  и , удовлетворяющие условию . Так как , то эти векторы должны быть независимыми; поэтому  - плоскость. Очевидно,

В частности,  регулярно, так как дискриминант отличен от нуля. Следовательно, ввиду (??) . Но  - также регулярное знакопеременное пространство. Первое утверждение следует теперь из соображений индукции. Второе тривиально следует из первого. Для доказательства третьего утверждения применяем (??). Теорема доказана.

База  регулярного знакопеременного пространства  называется гиперболической, если

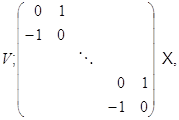
и симплектической, если

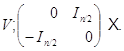
Если

 - гиперболическая база пространства , то перестановка

 - симплектическая база, и наоборот. По теореме (??) ненулевое регулярное знакопеременное пространство имеет гиперболическую базу, а потому и симплектическую базу.

Предложение  Пусть  - регулярное знакопеременное пространство,  - вполне вырожденное подпространство и  - база подпространства . Тогда существует регулярное подпространство  пространства  вида , где  - регулярные плоскости и , .

Доказательство. Случай  очевиден. При  применяем индукцию по . Положим  и . Тогда , откуда  ввиду (??). Выберем  и положим . Тогда , , и, следовательно, . Значит,  - регулярная плоскость, содержащая . В силу (??) можно записать . Тогда , так как  и  следовательно, . Остается применить предположение индукции к  рассматриваемому как подпространство знакопеременного пространства .

Предложение  Если  - максимальное вполне вырожденное подпространство регулярного знакопеременного пространства , то .

Доказательство. Так как  вполне вырождено, то , поэтому ввиду (??) , откуда . Если допустить, что , то несложное применение утверждений (??) и (??) даст вполне вырожденное подпространство, строго содержащее  в противоречие с максимальностью . Поэтому .

Предложение  Если  и  - максимальные вполне вырожденные подпространства регулярного знакопеременного пространства , удовлетворяющие условию , то для каждой базы  пространства М существует такая база  пространства , что  - симплектическая база пространства .

Доказательство. Разумеется,  (ввиду (??)). Пусть , - база подпространства . Тогда  - база пространства . Пусть  - сопряженная к ней база относительно  (см. (??)). Поскольку , то элементы  лежат в . Значит,  - база пространства , а

 - симплектическая база в .

Предложение  Пусть  - регулярное знакопеременное пространство и

 - его симплектическая база. Пусть  - максимальное вполне вырожденное пространство . Тогда матричный изоморфизм, ассоциированный с , отображает группу линейных преобразований

на группу матриц вида

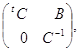
где  - обратимая -матрица, а -матрица  удовлетворяет соотношению .

Доказательство. Это легко проверяется надлежащим применением утверждения (??).

Теорема Теорема Витта Пусть  и  - изометричные регулярные знакопеременные пространства над одним и тем же полем . Если  - произвольное подпространство пространства  и  - изометрия  в , то ее можно продолжить до изометрии пространства  на .

Доказательство. Возьмем радикальное разложение , и пусть  - база подпространства  (имеется в виду, что , если ). Применяя (??) к регулярному знакопеременному пространству , мы видим, что в нем существует подпространство  вида

где  - регулярные плоскости и , . Так как  регулярно, то оно расщепляет ; следовательно, существует регулярное подпространство  пространства , такое, что

Положим ,  и  для . Тогда

Кроме того,

 - радикальное разложение. Мы можем повторить предыдущие рассуждения и получить разложение

в котором

где  - регулярная плоскость и  для . С помощью (??) найдем изометрию пространства  на , согласованную с  на каждом , а следовательно, на . Кроме того, данное  отображает  на . Значит, существует продолжение изометрии  до изометрии пространства  на . Далее , так как  изометрично , поэтому  и, следовательно, по теореме (??) существует изометрия пространства  на . Таким образом, существует продолжение изометрии  до изометрии пространства  на .

Проективные преобразования

Геометрическое преобразование  абстрактного векторного пространства  на абстрактное векторное пространство  - это биекция  со следующим свойством: подмножество  пространства  тогда и только тогда является подпространством в , когда  - подпространство в .

Очевидно, что композиция геометрических преобразований - геометрическое преобразование и преобразование, обратное к геометрическому, - также геометрическое. Геометрическое преобразование сохраняет включение, объединение и пересечение подпространств, а также ряды Жордана -- Гёльдера, поэтому справедливо следующее предложение.

Предложение  Если  - геометрическое преобразование пространства  на , то для любых подпространств ,  пространства  выполняются соотношения

Под проективным пространством  пространства  мы будем понимать множество всех подпространств пространства . Таким образом,  состоит из элементов множества , являющихся подпространствами в ;  - это частично упорядоченное множество, отношение порядка в котором индуцируется теоретико-множественным включением в . Любые два элемента  и  из  имеют объединение и пересечение, а именно  и , так что  - решетка; она имеет наибольший элемент  и наименьший элемент . Каждому элементу  пространства  сопоставляется число . Каждое  из  обладает рядом Жордана -- Гёльдера , и все такие ряды имеют длину . Положим

и назовем , ,  множествами прямых, плоскостей и гиперплоскостей пространства  соответственно.

Проективность  пространства  на  - это биекция  со следующим свойством: для любых ,  из  включение  имеет место тогда и только тогда, когда .

Очевидно, что композиция проективностей - проективность и отображение, обратное к проективности, - также проективность. Проективность пространства  на  сохраняет порядок, объединения, пересечения и ряды Жордана -- Гёльдера для элементов пространств  и , поэтому справедливо следующее предложение.

Предложение  Если  - проективность пространства  на , то для любых элементов ,  из  выполняются соотношения

В частности,  отображает  на  и определяется своими значениями на , т. е. на прямых.

Если  - геометрическое преобразование, то отображение , полученное из  сужением, является проективностью пространства  на . Всякая проективность , имеющая вид  для некоторого такого , будет называться проективным геометрическим преобразованием пространства  на . Черту мы будем всегда использовать для обозначения проективного геометрического преобразования , полученного описанным способом из геометрического преобразования . Таким образом,  переводит подпространство  пространства , т.е. точку  из , в подпространство  пространства . Имеем

В частности, композиция проективных геометрических преобразований и преобразование, обратное к проективному геометрическому, сами являются проективными геометрическими.

Геометрическое преобразование пространства  есть по определению геометрическое преобразование пространства  на себя. Множество геометрических преобразований пространства  является подгруппой группы подстановок множества . Она будет обозначаться через  и называться общей геометрической группой пространства . Под группой геометрических преобразований пространства  мы будем понимать произвольную подгруппу группы . Общая линейная группа  и специальная линейная группа  являются, следовательно, группами геометрических преобразований. Под группой линейных преобразований будем понимать любую подгруппу группы .

 Проективность пространства  есть по определению проективность этого пространства на себя. Множество проективностей пространства  - подгруппа группы подстановок множества , которую мы будем называть общей группой проективностей пространства . Применение черты индуцирует гомоморфизм

Иногда мы будем использовать  вместо , полагая

для образа  подмножества  из  при . В частности,  и  - подгруппы группы проективностей пространства , они называются проективной общей линейной группой и проективной специальной линейной группой пространства . Было доказано, что  совпадает с группой всех проективностей пространства , поэтому мы используем это обозначение для обеих групп. Под группой проективностей пространства  будем понимать любую подгруппу группы , а под проективной группой линейных преобразований пространства  - любую подгруппу группы .

Для каждого ненулевого элемента  из  определим линейное преобразование , полагая

Ясно, что . Преобразование  из  вида  для некоторого  будем называть растяжением пространства . Множество растяжений пространства  является нормальной подгруппой группы , которая будет обозначаться через . Очевидно, имеет место изоморфизм . Имеют место следующие два предложения.

Предложение  Элемент  группы  тогда и только тогда принадлежит группе , когда  для всех прямых  из . В частности,

и

Предложение  Централизатор в  любого элемента из , не являющегося растяжением, абелев.

Пусть теперь  - регулярное знакопеременное пространство. Тогда  будет, конечно, группой геометрических преобразований пространства . Под группой симплектических преобразований знакопеременного пространства  мы будем понимать произвольную подгруппу из . Группа , получаемая из  применением гомоморфизма , называется проективной симплектической группой знакопеременного пространства . Под проективной группой симплектических преобразований пространства  будем понимать любую подгруппу группы .

Предложение  Если  - ненулевое регулярное знакопеременное пространство, то

Доказательство является легким упражнением и потому опускается.

Предложение  Если  - регулярное знакопеременное пространство и , то .

Доказательство. Взяв симплектическую базу пространства , с помощью (??) без труда убеждаемся, что элемент  из  тогда и только тогда лежит в , когда .

Полярностью абстрактного векторного пространства  над полем  называется биекция , , такая, что

1) ,

2)

для всех ,  из . Если  - регулярное знакопеременное пространство над , то, очевидно,  - полярность; она называется полярностью, определенной знакопеременной формой , имеющейся на .

Предложение  Пусть  - абстрактное векторное пространство над полем  и . Предположим, что  - регулярное знакопеременное пространство относительно каждой из двух знакопеременных форм  и . Формы  и  тогда и только тогда определяют одну и ту же полярность, когда найдется такой ненулевой элемент  из , что .

Доказательство. Если , то утверждение очевидно. Остается доказать обратное утверждение. Так как  регулярно относительно  и , то ввиду (??) и (??) ассоциированные линейные отображения  и  биективны, т. е.  и . Из (??) и предположения о том, что  и  определяют одну и ту же полярность, следует, что  для всех подпространств  из . Следовательно,  - элемент группы , относительно которого инвариантны все подпространства из , В частности, относительно него инвариантны все прямые из . Значит, ввиду (??) . Другими словами, найдется такой ненулевой элемент  из , что  для всех  из . Но тогда  для всех  из . Поэтому .

Структурные теоремы. Порядки симплектических групп

Предложение  Если поле  бесконечно, то группы ,  над  также бесконечны.

Доказательство. Число трансвекций  из  бесконечно.

Теорема  Порядок группы  равен

Порядок группы  равен

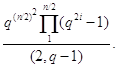
Доказательство. Второе утверждение следует из первого, так как группа  изоморфна группе . Докажем первое утверждение индукцией по . Если , то  и можно считать .

Под парой будем понимать упорядоченную пару векторов , , такую, что . Если  фиксирован, то существует единственная пара , где  принадлежит данной прямой, не ортогональной к . Поэтому число пар с  на первом месте равно числу прямых, не лежащих в , т. е.

Таким образом, имеется  пар с  на первом месте, а всего  пар.

Зафиксируем какую-нибудь пару . По теореме Витта для каждой пары  найдется по крайней мере один элемент группы , переводящий  в . Следовательно, имеется точно

элементов из , переводящих пару  в пару . По предположению индукции это число равно

Далее, каждый элемент группы  переводит  точно в одну пару. Следовательно, группа  содержит

элементов, что и требовалось доказать.

Предложение Если , то число максимальных вполне вырожденных подпространств пространства  равно

Доказательство. 1) Покажем сначала, что подгруппа  группы , оставляющая на месте произвольное максимальное вполне вырожденное подпространство  пространства , имеет порядок

Чтобы убедиться в этом, зафиксируем симплектическую базу

пространства , в которой векторы  порождают . Из (??) следует, что матрица произвольного преобразования  имеет вид

где , а  - симметрическая матрица порядка  над ; эти  и  определяются преобразованием  однозначно. Кроме того, любые такие  и  соответствуют некоторому  из . Наше утверждение получается теперь, если умножить порядок группы  на число симметрических матриц порядка  над полем , т. е. .

2) Зафиксируем максимальное вполне вырожденное подпространство  пространства . По теореме Витта все максимальные вполне вырожденные подпространства пространства  даются формулой , где  пробегает группу . Из замечания 1) легко следует, что в этом процессе каждое максимальное вполне вырожденное подпространство повторяется точно

раз, поэтому общее число таких подпространств равно порядку группы , деленному на указанную величину. Очевидно, это и есть требуемое число.

Предложение  Если , то число регулярных плоскостей в пространстве  равно

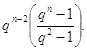
Доказательство. Поступая, как при доказательстве утверждения (??), убедимся, что  должно содержать

регулярных плоскостей. Это число совпадает с указанным выше (применить теорему (??)).

Предложение  Группа  изоморфна симметрической группе .

Доказательство. Будем называть конфигурацией произвольное подмножество  из  элементов в -мерном регулярном знакопеременном пространстве  над полем , обладающее тем свойством, что любые два его различных элемента не ортогональны. Каждый ненулевой вектор  из  принадлежит ровно двум конфигурациям  и , так что они пересекаются по . Чтобы убедиться в этом, возьмем симплектическую базу  пространства , в которой . Ясно, что

и

- две различные конфигурации, пересекающиеся по множеству . Легкая проверка перебором показывает, что других конфигураций, содержащих элемент , нет. Если теперь выписать все различные конфигурации  в пространстве , то каждый вектор  из  появится точно в двух из них, откуда  и . Пусть  - Множество всех конфигураций в .

Если  - произвольный элемент из , то  тогда и только тогда является конфигурацией, когда  - конфигурация, поэтому  индуцирует отображение . Ясно, что это отображение на и, значит, перестановка на . Очевидно, что  есть гомоморфное отображение . Чтобы найти его ядро, возьмем в  элемент . Пусть  таков, что . Пусть  и  - две конфигурации, содержащие . Тогда  не принадлежит одной из них, скажем, . Отсюда  и . Другими словами, ядро тривиально, и мы имеем инъективный гомоморфизм . По теореме (??) группа  состоит из  элементов, поэтому .

Центры

Заметим, что группа  неабелева. Чтобы убедиться в этом, достаточно взять нетривиальные проективные трансвекции из  с неортогональными вычетными прямыми. Следовательно, группа  также неабелева.

Предложение  Группа  имеет тривиальный центр, а .

Доказательство. Рассмотрим произвольный элемент  из центра группы . Пусть  - произвольная прямая из . Пусть  - проективная трансвекция из  с вычетной прямой . Тогда вычетной прямой преобразования  является . Но , так как  лежит в центре. Следовательно,  для всех . Поэтому  и, значит, группа  действительно не имеет центра. Второе утверждение следует из первого, если применить гомоморфизм .

Коммутанты

Предложение  Если ,  - произвольные прямые из , то множество трансвекций из  с вычетной прямой  и множество трансвекций с вычетной прямой  сопряжены относительно .

Доказательство. По теореме Витта в группе  существует такой элемент , что . Тогда сопряжение элементом  отображает множество трансвекций из  с вычетной прямой  на множество трансвекций из  с вычетной прямой .

Пример  Две трансвекций из  не обязательно сопряжены в . Например, трансвекций с вычетной прямой , сопряженные с , имеют вид , где  пробегает .

Замечание  Пусть  - симплектическая база пространства . Если  - произвольная симметрическая матрица порядка 2 над  и  - линейное преобразование, определенное матрицей

то мы знаем, что  принадлежит группе . Если преобразовать  в , производя 1) прибавление кратного одного столбца к другому с последующим аналогичным преобразованием соответствующих строк или 2) перестановку двух столбцов с последующей перестановкой соответствующих строк, то линейное преобразование  с матрицей

снова будет принадлежать группе , так как  тоже будет симметрической. В действительности  и  сопряжены в . Чтобы убедиться в этом, заметим, что  при подходящей матрице  из . Преобразование , определенное матрицей

принадлежит группе , и , так как

Предложение  Предположим, что , ,  и пусть  - нормальная подгруппа группы , содержащая регулярный элемент  с вычетом , представимый в виде произведения двух трансвекций из . Тогда .

Доказательство. Имеем разложение , где  - регулярная плоскость. Рассмотрим группу

Тогда . Кроме того, . Это очевидно, если ; если же , то применяем 2.1.12 и теорему 2.1.11 [??]. Поэтому  - нормальная подгруппа в , не содержащаяся в . Отсюда следует, что . В частности, если  - фиксированная прямая в , то  содержит все трансвекции плоскости  с вычетной прямой . Следовательно,  содержит все трансвекции из  с вычетной прямой , а потому в силу (??) вообще все трансвекции из  и .

Предложение  Предположим, что ,  или , , и пусть  - нормальная подгруппа группы , содержащая вырожденный элемент  с вычетом 2, представимый в виде произведения двух трансвекций из . Тогда .

Доказательство. 1) Модификация рассуждений, использованных при доказательстве утверждения (??), позволяет считать, что , если , и , если .

2) Рассмотрим сначала случай , . Тогда  имеет вид , причем , а звездочки равны . Далее эти трансвекции перестановочны, так как , поэтому мы можем, если нужно, заменить  на  и считать, что на самом деле . Можно считать, что эта новая  есть . В самом деле, если , то с помощью теоремы Витта выберем такое , что , . Тогда

Заменим теперь  на

Итак, можно считать, что . Дополним  до симплектической базы

пространства  и заметим, что

Подходящим сопряжением мы можем найти в  линейные преобразования с матрицами

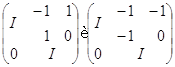
в базе . Произведение этих преобразований равно элементу из  с матрицей

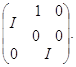
Следовательно, группа  содержит . Таким образом, она содержит все (= обе) трансвекции из  с вычетной прямой . Ввиду (??) отсюда следует, что  содержит все трансвекции из  и, значит, .

3) Пусть теперь , . Тогда  и . Дополним  до симплектической базы

Тогда

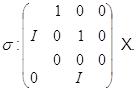
Сопряжение дает нам в  линейные преобразования с матрицами

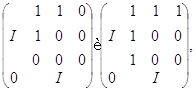
а потому и с матрицами

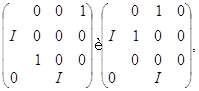
а значит, и с матрицей

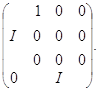
Другими словами,  содержит  и, следовательно, все трансвекции из , откуда .

Предложение  Если , то  за одним исключением: .

Доказательство. Пусть , для некоторого . По теореме Витта существует такое , что  - плоскость и

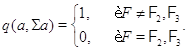
Положим

Осталось применить (??) и (??). В исключительном случае применяем (??) и хорошо известные свойства группы .

Предложение  Если , то  за одним исключением: .

  Теоремы о простоте

Теорема  Для любого четного числа  и любого поля  группа  проста за исключением группы , которая простой не является.

Доказательство. 1) Исключительное поведение группы  следует из (??). Будем предполагать поэтому, что  в общем случае и  при . Вместо проективной группы мы будем иметь дело с группой . Достаточно рассмотреть нормальную подгруппу  группы , не содержащуюся в подгруппе , и доказать, что .

2) Сначала покажем, что имеются , , такие, что  - регулярная плоскость. Для этого возьмем в группе  элемент .  сдвигает по крайней мере одну прямую из , т. е. существует такая прямая  из , что . Пусть  - нетривиальная трансвекция из  с вычетной прямой . Тогда элемент

принадлежит группе  и является произведением двух трансвекции из  с различными вычетными прямыми  и . Поэтому вычетное пространство преобразования  есть плоскость , в частности, . Если  - гиперболическое преобразование, то  - инволюция. Применим теперь утверждение 1.18, если характеристика равна , и утверждение 1.13, если характеристика не равна . Тогда, в частности, мы получим, что  не является произведением  трансвекции из , что противоречит допущению. Итак,  не может быть гиперболическим. Значит, существует такой вектор , что , т. е.  - регулярная плоскость.

3) Можно также показать, что имеются вектор  и преобразование , такие, что  - вырожденная плоскость. В самом деле, возьмем в  элемент . Существует такой вектор , что . Если , то цель достигнута, поэтому будем считать, что . Выберем  так, чтобы было

По теореме Витта в  найдется преобразование , такое, что , . Тогда преобразование  принадлежит  и переводит  в , поэтому  - вырожденная плоскость.

4) Возьмем ,  так, чтобы плоскость  была регулярной при  и вырожденной при . Тогда преобразование

принадлежит группе , является произведением двух трансвекций из  и его вычетное пространство есть плоскость . Поэтому .

Предложение  Если  и  - нормальная подгруппа группы , то  или , за исключением группы , которая, очевидно, не обладает этим свойством.

Доказательство. По поводу исключения см. (??). Далее, применяя к  теорему (??), получим, что  или . Допустим последнее. Тогда

Предложение доказано.

Теорему о простоте можно также доказать, используя группы подстановок. Напомним, что группой подстановок непустого множества  называется подгруппа  группы всех подстановок множества . Далее,  называется транзитивной, если для любых ,  существует такая подстановка  из , что . Напомним, что разбиением множества  называется множество  попарно непересекающихся подмножеств, объединение которых равно . Тривиальными называются два разбиения, состоящие соответственно из самого  и из всех одноэлементных подмножеств. Транзитивная группа  подстановок множества  называется импримитивной, если существует такое нетривиальное разбиение  множества , что  для всех , . В противном случае группа называется примитивной. Следующий результат является здесь ключевым.

Предложение  Примитивная группа подстановок  множества  проста, если выполнены следующие условия:

1) ,

2) для некоторого  стабилизатор  содержит такую нормальную абелеву подгруппу , что  порождается подгруппами , .

Для доказательства теоремы (??) с использованием этого результата рассмотрим  как группу подстановок множества прямых  пространства . Это возможно ввиду того, что , будучи подгруппой группы проективностей пространства , точно действует на  и, значит,  естественно изоморфна группе подстановок множества . Мы знаем, что группа  транзитивна (теорема Витта),  (см. (??)) и, наконец, множество проективных трансвекций из  с вычетной прямой  вместе с тождественным преобразованием образует нормальную абелеву подгруппу стабилизатора прямой  в , которая вместе со своими сопряженными в  порождает группу . Поэтому все, что осталось сделать, прежде чем сослаться на (??), - это проверить, что группа  примитивна.

Предложение  При  группа  подстановок множества  прямых пространства  примитивна.

Доказательство. 1) Рассмотрим разбиение  множества , содержащее по крайней мере два подмножества, одно из которых, скажем , содержит не менее двух прямых. Нам нужно найти элемент группы , не сохраняющий это разбиение. Допустим, что такого элемента не существует.

2) Пусть сначала  содержит две различные не ортогональные прямые , . Тогда каждые две различные прямые ,  из  должны быть не ортогональны. В самом деле, если это не так, то найдутся различные ,  из , такие, что . Возьмем прямую  из , не принадлежащую подмножеству . Если , то по теореме Витта существует такое преобразование  из , что , , и, следовательно, оно нарушает разбиение. Если , то снова по теореме Витта имеется такое , что ,  и, значит,  опять нарушает разбиение. Итак, никакие две различные прямые из  не является ортогональными. Только что проведенные рассуждения показывают, что если  - произвольная прямая из , то  содержит все прямые из , не ортогональные к . Теперь очевидно, что можно найти в  прямую , не ортогональную к , но ортогональную к  тогда первое условие влечет за собой, что , а второе - что , - противоречие.

3) Мы можем, таким образом, считать, что все прямые из  попарно ортогональны. Рассуждения, использованные в п. 2), показывают тогда, что если  - произвольная прямая из , то  содержит все прямые, ортогональные к , а это невозможно. Предложение доказано.

Основные результаты

Пусть  - конечная группа,  и  - подгруппы группы . Будем говорить, что группа  допускает факторизацию , если для всякого  имеет место равенство , где , . Факторизация называется максимальной, если  и  максимальные подгруппы в группе . Мы рассмотрим максимальные факторизации симплектической группы , определенной над конечным полем .

Пусть  и  - целые числа, , . Если  - простое число, делящее  и не делящее числа  для , то  называют примитивным простым делителем числа .

Хорошо известно, что при ,  и  всегда есть примитивный простой делитель числа . Пусть , где  - простое число,  - целое положительное число. Обозначим  наибольший примитивный простой делитель числа  (так, что  делит  и не делит  для ). Определим  как произведение всех примитивных простых делителей . Мы будем рассматривать максимальные факторизации группы . Отметим, что

 

Теорема Пусть , где  - нечетное число. Если , где  и  - максимальные подгруппы группы , тогда , где  - максимальная параболическая подгруппа группы , изоморфная  и имеющая порядок

Доказательство. Предположим, что  делит . Из [??] следует, что  является одной из следующих групп , ,  или . Пусть сначала . В этом случае . Из [??] следует, что  это в точности максимальная параболическая подгруппа группы   и . Из сравнения порядков группы  и произведения  получаем следующую максимальную факторизацию:

Пусть теперь  является одной из следующих групп ,  или . Из сказанного выше следует, что  не изоморфна . Из пункта 2.4 [??] получим, что  есть  или . По теореме 2.4D [??]  есть 3 или 7. Если , тогда 5 делит . В этом случае из [??] следует, что  одна из групп , , . Поскольку , то  делит . Однако  не делится на . Противоречие с тем, что . Следовательно,  и . Так как 27 делит , то  является параболической подгруппой группы  и имеет место факторизация:

Теорема (??) доказана.

Пусть , где  - положительное число. Тогда ортогональная группа  и .  обозначает сплетение группы  с группой , т.е. , где . Очевидно, что ;  - максимальная параболическая подгруппа в  порядка ;  - группа Судзуки порядка , где .

Лемма  Пусть . Тогда

Доказательство. Из [??] следует, что  является максимальной подгруппой в . Пусть  и . Обозначим

где  матрица в каноническом базисе симплектического пространства , , , . Тогда  - диэдральная группа, которая фиксирует разложение:

Из [??] следует, что стабилизатор этого разложения ,  и

Лемма доказана.

В приведенных обозначениях с учетом таблицы 1 [??] и леммы (??) получим:

Теорема  Пусть , где . Если , где  и  - максимальные подгруппы в группе . Тогда

1) ,

2) ,

3) ,

4) ,

5) .

Заключение

 

В дипломной работе найдены максимальные факторизации симплектических групп . Доказаны следующие теоремы.

Теорема 1. Пусть , где  - нечетное число. Если , где  и  - максимальные подгруппы группы , тогда , где  - максимальная параболическая подгруппа группы , изоморфная  и имеющая порядок

Теорема 2. Пусть , где . Если , где  и  - максимальные подгруппы в группе . Тогда

 

1) ,

2) ,

3) ,

4) ,

5) .

Список использованных источников

[1] Монахов В.С. Введение в теорию конечных групп и их классов, Гомель: Гомельский государственный университет им. Ф.Скорины, 2003. - 320 с.

[2] Каргаполов М.И., Мерзляков Ю.И., Основы теории групп, М., 1982.

[3] Холл Ф., Теория групп, М., 1962.

[4] Горенстейн Д., Конечные простые группы: введение в их классификацию., М., 1985.

[5] Казарин Л.С., Факторизации конечных групп разрешимыми подгруппами //Укр. мат. журн. 1991. Т. 43, N 7 -- 8. С. 947 -- 950.

[6] Mitchel H.H., Determination of the finite quaternary linear groups. Trans. Amer. Math. Soc. V. 14, 1913. p.123--142.

[7] Liebek M.W., Praeqer C.E., Saxl J., The maximal factorizations of the finite simple groups and their automorphism groups. Mem. Amer. Math. Soc. V. 86, N. 432. p. 1--151.

[8] Suzuki M., A new type of simple groups of finite order. Proc. Nat. Acad. Sci. US 46, 1960. p. 868--870.