Навигация
Постановка и основные свойства транспортной задачи
Транспортная задача (Т-задача) является одной из наиболее распространенных специальных задач ЛП. Частные постановки задачи рассмотрены рядом специалистов по транспорту, например О.Н. Толстым [18; 59].
Первая строгая постановка Т-задачи принадлежит Ф. Хичкоку, поэтому в зарубежной литературе ее называют проблемой Хичкока.
Первый точный метод решения Т-задачи разработан Л.В. Канторовичем и М.К. Гавуриным.
Постановка Т-задачи. Пусть в пунктах А1,…, Am производят некоторый однородный продукт, причем объем производства в пункте Ai составляет ai единиц, i = 1,…, m. Допустим, что данный продукт потребляют в пунктах B1., Bn, a объем потребления в пункте Вj составляет bj одиниць j = 1., n. Предположим, что из каждого пункта производства возможно транспортировка продукта в любой пунктпотребления. Транспортные издержки по перевозке единицы продукции из пункта Ai в пункт Вj равны cij (i = 1., m; j = 1., n). Задача состоит в определении такого плана перевозок, при котором запросы всех потребителей Вj полностью удовлетворены, весь продукт из пунктов производства вывезен и суммарные транспортные издержки минимальны.
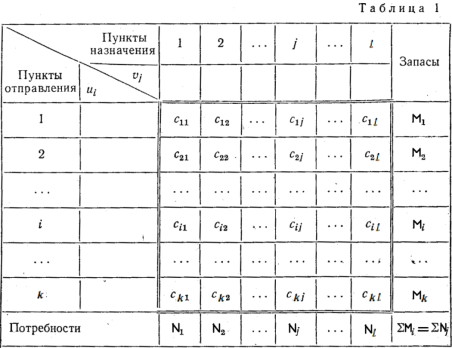
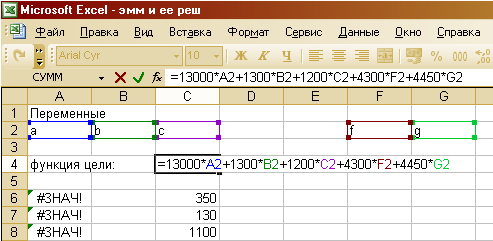
Условия Т-задачи удобно представить в виде табл. 1.1. Таблица. 1.1.| Пункт потребления Пункт производства | B1 | B2 | . | Bn | Bj ai |
| A1 | C11 | C12 | . | C1n | a1 |
| A2 | C21 | C22 | . | C2n | a2 |
| Am | Cm1 | Cm2 | . | Cmn | am |
| Ai bj | b1 | b2 | . | bn | Объем производства Объем потребления |
Пусть ![]() количество продукта, перевозимого из пункта Ai в пункт Вj.
количество продукта, перевозимого из пункта Ai в пункт Вj.
Требуется определить множество переменных ![]() , i = 1., m, j = 1., n, удовлетворяющих условиям
, i = 1., m, j = 1., n, удовлетворяющих условиям
![]() (1.1)
(1.1)
![]() (1.2)
(1.2)
и таких, что целевая функция
![]() (1.3)
(1.3)
достигает минимального значения.
Условие (1.1) гарантирует полный вывоз продукта из всех пунктов производства, а (1.2) означает полное удовлетворение спроса во всех пунктах потребления.
Таким образом, Т-задача представляет собой задачу ЛП с ![]() числом переменных, и (m + n) числом ограничений равенств.
числом переменных, и (m + n) числом ограничений равенств.
Переменные ![]() удобно задавать в виде матрицы
удобно задавать в виде матрицы
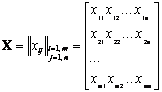 (1.4)
(1.4)
Матрицу X, удовлетворяющую условиям Т-задачи (1.1) и (1.2) называют планом перевозок, а переменные ![]() – перевозками. План
– перевозками. План ![]() , при котором целевая функция минимальна, называется оптимальным, а матрица С=
, при котором целевая функция минимальна, называется оптимальным, а матрица С= ![]() – матрицей транспортных затрат.
– матрицей транспортных затрат.
Графический способ задания Т-задач показан на рис. 1
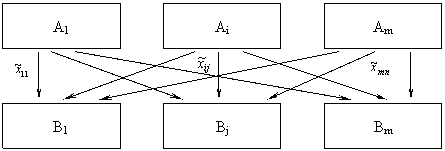
Рис. 1
Отрезок AiBj называют коммуникацией. На всех коммуникациях ставят величины перевозок xij.
Вектор Pij, компоненты которого состоят из коэффициентов при переменных xij в ограничениях (3.1.1) и (3.1.2), называют вектором коммуникаций:
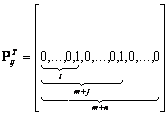
Вводят также вектор производства-потребления P0, где
![]() .
.
Тогда ограничение (3.1.1) и (3.1.2) можно записать в векторной форме
![]() , (1.5)
, (1.5)
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... ) является необходимым и достаточным для существования решения транспортной задачи. Лист Кп-км-п-44-2203-99 4. Анализ задачи или модели. 4.1 Определение опорного плана транспортной задачи Для решения транспортной задачи разработано несколько методов, каждый из которых отличается от другого методом заполнения матрицы перевозок. Существуют два ...
... метод потенциалов. Однако на распределительном методе основаны некоторые другие способы решения задач, что и вызывает необходимость его изучения. [5] 9. Метод потенциалов Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид. Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая ...
... : - каждому виду продукции должна соответствовать одна транспортная матрица; - все виды продукции представлены в одной общей матрице с использованием запрещающих тарифов в клетках, связывающих разные виды продукции. 3.2 Решение транспортной задачи на примере ООО «Дубровчанка+» Применяя теорию транспортной задачи к показателям работы ООО «Дубровчанка +», составим следующую транспортную ...





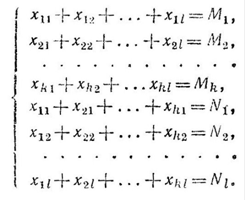

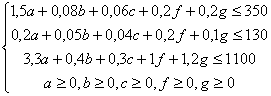
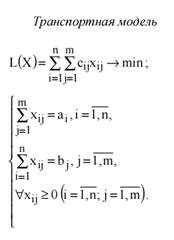
0 комментариев