Навигация
Методы линейного программирования для решения транспортной задачи
План реферата
Введение
1. Формулировка транспортной задачи
2. Математическая модель транспортной задачи
3. Необходимое и достаточное условия разрешимости транспортной задачи
4. Свойство системы ограничений транспортной задачи
5. Опорное решение транспортной задачи
6. Методы построения начального опорного решения
6.1 Построение первоначального плана по способу северо-западного угла
6.2 Построение первоначального плана по способу минимального элемента
7. Переход от одного опорного решения к другому
8. Распределительный метод
9. Метод потенциалов
10. Особенности решения транспортных задач с неправильным балансом
11. Алгоритм решения транспортной задачи методом потенциалов
11.1 Предварительный шаг
11.2 Общий повторяющийся шаг
12. Транспортная задача с ограничениями на пропускную способность
13. Транспортная задача по критерию времени
14. Применение транспортной задачи для решения экономических задач
Заключение
Список использованной литературы
Введение
Методы линейного программирования применяются для решения многих экстремальных задач, с которыми довольно часто приходится иметь дело в экономике. Решение таких задач сводится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин.
Линейное программирование основано на решении системы линейных уравнений (с преобразованием в уравнения и неравенства), когда зависимость между изучаемыми явлениями строго функциональна. Для него характерны математическое выражение переменных величин, определенный порядок, последовательность расчетов (алгоритм), логический анализ. Применять его можно только в тех случаях, когда изучаемые переменные величины и факторы имеют математическую определенность и количественную ограниченность, когда в результате известной последовательности расчетов происходит взаимозаменяемость факторов, когда логика в расчетах, математическая логика совмещаются с логически обоснованным пониманием сущности изучаемого явления.
С помощью этого метода в промышленном производстве, например, исчисляется оптимальная общая производительность машин, агрегатов, поточных линий (при заданном ассортименте продукции и иных заданных величинах), решается задача рационального раскроя материалов (с оптимальным выходом заготовок). В сельском хозяйстве он используется для определения минимальной стоимости кормовых рационов при заданном количестве кормов (по видам и содержащимся в них питательным веществам). Задача о смесях может найти применение и в литейном производстве (состав металлургической шихты). Этим же методом решаются транспортная задача, задача рационального прикрепления предприятий-потребителей к предприятиям-производителям.
Все экономические задачи, решаемые с применением линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями. Решить такую задачу - значит выбрать из всех допустимо возможных (альтернативных) вариантов лучший, оптимальный. Важность и ценность использования в экономике метода линейного программирования состоят в том, что оптимальный вариант выбирается из весьма значительного количества альтернативных вариантов. При помощи других способов решать такие задачи практически невозможно.
Весьма типичной задачей, решаемой с помощью линейного программирования, является транспортная задача. [1]
Транспортная задача (transportation problem) - одна из наиболее распространенных задач математического программирования (обычно - линейного). В общем виде ее можно представить так: требуется найти такой план доставки грузов от поставщиков к потребителям, чтобы стоимость перевозки (или суммарная дальность, или объем транспортной работы в тонно-километрах) была наименьшей. Следовательно, дело сводится к наиболее рациональному прикреплению производителей к потребителям и наоборот. [2]
1. Формулировка транспортной задачи
В простейшем виде, когда распределяется один вид продукта и потребителям все равно, от кого из поставщиков его получать, задача формулируется следующим образом.
Исходная информация:
Mi - количество единиц груза в i-м пункте отправления (i = 1, 2, …, k);
Nj - потребность в j-м пункте назначения (j = 1, 2, …, l) (в единицах груза);
aij - стоимость перевозки единицы груза из i-гo пункта в j-й.
Обозначим через xij планируемое количество единиц груза для перевозки из i-ro пункта в j-й.
В принятых обозначениях:
![]() - общая (суммарная) стоимость перевозок;
- общая (суммарная) стоимость перевозок;
![]() - количество груза, вывозимого из i-ro пункта;
- количество груза, вывозимого из i-ro пункта;
![]() - количество груза, доставляемого в j-и пункт.
- количество груза, доставляемого в j-и пункт.
В простейшем случае должны выполняться следующие очевидные условия:
![]()
![]()
![]()
Таким образом, математической формулировкой транспортной задачи будет:
найти
![]()
при условиях
![]() ;
;
![]() ;
;
![]()
Эта задача носит название замкнутой (закрытой, сбалансированной) транспортной модели.
Заметим, что условие ![]() является естественным условием разрешимости замкнутой транспортной задачи.
является естественным условием разрешимости замкнутой транспортной задачи.
Более общей транспортной задачей является так называемая открытая (несбалансированная) транспортная модель:
найти
![]()
при условиях
![]()
![]()
![]()
Ясно, что в этой задаче не предполагается, что весь груз, накопленный в i-м пункте, должен быть вывезен. [3]
2. Математическая модель транспортной задачи
Простейшими транспортными задачами являются задачи о перевозках некоторого однородного груза из пунктов отправления (от поставщиков) в пункты назначения (к потребителям) при обеспечении минимальных затрат на перевозки.
Обычно начальные условия таких задач записывают в таблицу. Например, для k поставщиков и l потребителей такая задача имеет следующий вид:
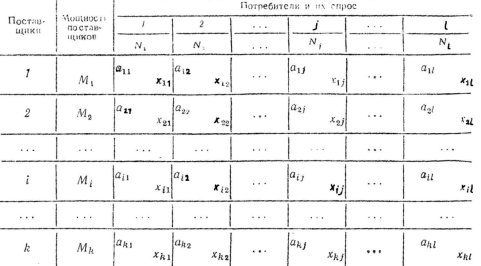
Здесь показатели aij означают затраты на перевозку единицы груза от i-го поставщика (i=1,2,…,k) к j-тому потребителю (j=1,2,…,l), Mi - мощность i-того поставщика в планируемый период, Nj - спрос j-того потребителя на этот же период. Обозначим через xij поставку (количество груза), которая планируется к перевозке от i-того поставщика к j-тому потребителю. Математически задача сводится к нахождению минимума целевой функции, выражающей суммарные затраты на перевозку груза, т.е. функции
![]()
при ограничениях
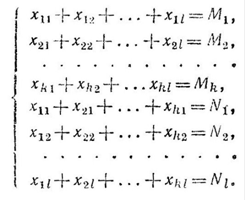 (1)
(1)
Если к этим ограничениям добавить еще одно:
![]() ,(2)
,(2)
т.е. суммарная мощность поставщиков равна суммарному спросу потребителей, то соответствующая модель задачи называется закрытой.
Задачам, в которых ограничение (2) отсутствует, т.е.
![]() ,
,
первоначально соответствует открытая модель.
Отметим некоторые особенности экономико-математической модели транспортной задачи.
Система ограничений (1) сразу имеет вид уравнений, поэтому отпадает необходимость вводить добавочные переменные.
Матрица коэффициентов при переменных в системе (1) состоит только из единиц и нулей.
Система ограничений (1) включает k уравнений, связывающих поставки i-того поставщика с мощностью Mi (i=1,2,…,k) этого поставщика, и l уравнений, связывающих поставки j-тому потребителю со спросом Nj (j=1,2,…,l) этого потребителя. Заметим, что число k равно числу строк исходной таблицы, а число l - числу столбцов.
Число переменных xij, входящих в целевую функцию и в систему уравнений (1), равно произведению kl, т.е. числу клеток таблицы.
Таким образом, система ограничений (1) есть система из k+l уравнений с kl переменными.
Любое решение транспортной задачи (x11, x12,…, xkl) называется распределением поставок. Так как поставки не могут быть отрицательными, то речь идет только о допустимых решениях.
Оптимальному решению транспортной задачи соответствует оптимальное распределение поставок, при котором целевая функция ![]() достигает своего минимума.
достигает своего минимума.
В ходе решения задачи и нужно получить это оптимальное распределение поставок, которому соответствует какое-то допустимое базисное решение системы ограничений (1). [4]
3. Необходимое и достаточное условия разрешимости транспортной задачи
Ограничение (1) и условия неотрицательности переменных, исключающие обратные перевозки xij>0; i= 1, 2, …, k; j= 1, 2,., l.
Эти условия образуют систему ограничений. Любой план, компоненты которого удовлетворяют этой системе, будет допустимым.
Как видим, система ограничений задана в основном (k + l) уравнениями. Установим условия, при которых эта система будет совместной, т.е. будет иметь решения.
Сложим элементы xij матрицы перевозок по строкам, каждая строка в сумме дает Mi, и в итоге получим ![]() . Сложим те же элементы по столбцам, каждый столбец дает Nj, и в сумме получим
. Сложим те же элементы по столбцам, каждый столбец дает Nj, и в сумме получим ![]() . Но от перестановки слагаемых сумма не меняется, поэтому для любого допустимого плана обязательно будет выполняться условие
. Но от перестановки слагаемых сумма не меняется, поэтому для любого допустимого плана обязательно будет выполняться условие
![]() .
.
Равенство ![]() является необходимым условием совместности ограничений задачи.
является необходимым условием совместности ограничений задачи.
Докажем и достаточность этого условия: если запасы равны потребностям, то всегда имеется допустимый план.
Действительно, пусть ![]() . Рассмотрим такие числа:
. Рассмотрим такие числа:
![]()
Убедимся, что эти числа образуют допустимый план. Для этого достаточно проверить, что они удовлетворяют всем ограничениям задачи.
Просуммируем эти числа по индексу i:
![]() .
.
Но величины Nj,![]() от индекса i не зависят и их можно вынести за знак суммы. В результате
от индекса i не зависят и их можно вынести за знак суммы. В результате
![]()
или
![]() ,
, ![]()
Следовательно, взятые числа удовлетворяют группе уравнений (1).
Просуммируем эти числа по индексу j:
![]()
Вынося постоянные Mi и ![]() за знак суммы и имея в виду, что
за знак суммы и имея в виду, что ![]() , получаем
, получаем
![]()
или в развернутом виде
![]()
Как видим, наши числа удовлетворяют группе уравнений (1). Эти числа неотрицательны, т.е. система ограничений полностью удовлетворяется. Таким образом, допустимый план существует, что и требовалось доказать.
Равенство запасов потребностям есть необходимое и достаточное условие совместности и, следовательно, разрешимости транспортной задачи. [5]
4. Свойство системы ограничений транспортной задачи
Согласно теореме о структуре координат опорного плана задачи линейного программирования, в невырожденном опорном плане должно содержаться r отличных от нуля координат, где r - ранг системы ограничений
![]() .
.
В этой системе ограничений уравнений закрытой транспортной задачи имеется k+l-1 линейно-независимых уравнений, т.е. ранг системы ограничений равен k+l-1. [6]
5. Опорное решение транспортной задачи
Опорное решение (опорный план, базисное решение, basic solution) - одно из допустимых решений, находящихся в вершинах области допустимых решений. Оно является решением системы линейных ограничений, которое нельзя представить в виде линейной комбинации никаких других решений.
При решении задачи линейного программирования можно поступить следующим образом: найти любое из таких "вершинных" решений, не обязательно оптимальное, и принять его за исходный пункт расчетов. Такое решение и будет базисным. Если окажется, что оно и оптимальное, расчет на этом закончен, если нет - последовательно проверяют, не будут ли оптимальными соседние вершинные точки. Ту из них, в которой план эффективнее, принимают снова за исходную точку и так, последовательно проверяя на оптимальность аналогичные вершины, приходят к искомому оптимуму. На этом принципе строятся так называемый симплексный метод решения задач линейного программирования, а также ряд других способов, объединенных общим названием "методы последовательного улучшения допустимого решения (МПУ)": метод обратной матрицы, или модифицированный симплекс-метод, метод потенциалов для транспортной задачи и другие. Они отличаются друг от друга вычислительными особенностями перехода от одного базисного решения к другому, улучшенному. [2]
6. Методы построения начального опорного решения 6.1 Построение первоначального плана по способу северо-западного угла
В этом случае не обращают внимания на показатели затрат. Начав заполнение с клетки (1.1) - "северо-западного угла" таблицы, ступенями спускаются вниз до клетки (k, l), вычеркивая либо одну строку, либо один столбец. На последнем шаге вычеркиваются последняя (k-я) строка и последний (l-й) столбец. При практическом заполнении таблицы, вычеркивание строк и столбцов производится лишь мысленно.
Когда осуществляется первоначальное распределение поставок, то не ставится цель получить оптимальное распределение. Достижению этой цели служат последующие этапы решения задачи. Они заключаются в переходах к новым распределениям поставок, пока не будет найдено оптимальное распределение поставок. [4]
6.2 Построение первоначального плана по способу минимального элементаПри построении первоначального плана по способу северо-западного угла совершенно не учитываются тарифы, потому план получается весьма далеким от оптимального. Для решения задачи приходится делать много приближений (шагов).
Способ минимального элемента учитывает тарифы и потому позволяет найти план, более близкий к оптимальному.
Этот способ заключается в следующем.
Похожие работы
... во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные. 2. Области применения и ограничения использования линейного программирования для решения экономических задач Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации. Формулировка задачи линейного программирования Нужно максимизировать при условиях при i = 1, 2, 3, . . ., m.. Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от ...
... решений системы уравнений (3. ) и (3.) найти решение, минимизирующее линейную функцию (3. ). Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без симплекс-таблиц. Решение можно получить путем некоторых преобразований таблицы перевозок. Эти преобразования ...






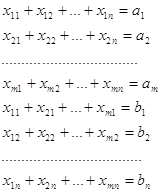
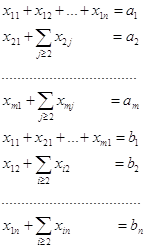
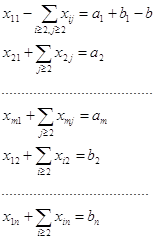
0 комментариев