Программирование на сетях

Содержание:

Введение. 2

1. Основные понятия теории графов. 3

2. Матричные способы задания графов. 4

3. Упорядочение элементов орграфа. 6

4. Постановка задачи о максимальном потоке. Основные определения. 8

5. Разрез на сети. 11

6. Алгоритм решения задачи о максимальном потоке. 13

Заключение. 20

Список использованной литературы.. 21

Введение

В последнее время в различных областях знаний широко применяется теория графов. С помощью теории графов хорошо описываются задачи экономической и планово-производственной практики, как, например, календарное и сетевое планирование и управление, автоматизация управления производством, рационализация схем перевозок и грузопотоков, оптимальное размещение производства т.п.

1. Основные понятия теории графов

Основным объектом этой теории является граф. Наглядно граф можно представить как некоторое множество точек плоскости или пространства и множество отрезков кривых или прямых линий, соединяющих все или некоторые из этих точек. Формально граф G определяется заданием двух множеств X и U и обозначается G=(XU). Элементы xB_1B, xB_2B, …, xB_nB множества X называются вершинами и изображаются точками. Элементами uB_1B, uB_2B, …, uB_mмножества U являются пары связанных между собой элементов множества X и изображаются отрезками. Взаимное расположение, форма и длины отрезков значения не имеют. Если в паре вершин xB_iBи B _BxB_jBуказано направление связи, то есть указано, какая вершина является первой, то отрезок UB_{1 B}называется дугой, а если ориентация не указана, - ребром.

Если в графе G все элементы множества U изображаются дугами, то граф называется ориентированным (орграф), если ребрами, - неориентированным.

На практике используются графы, в которых множества X и U состоят из конечного числа элементов, то есть конечные графы. На рисунке располагать вершины графа можно произвольно. Также произвольно выбирается и форма соединяющих их линий. Поэтому один и тот же граф (граф с одной и той же информацией) может быть представлен в различных видах. Такие графы называются изоморфными.

Смежными называют вершины графа, если они различны и существует дуга (ребро), которая соединяет эти вершины. Если две дуги (ребра) имеют общую концевую вершину, то такие дуги (ребра) смежные.

Последовательность дуг, в которой конец каждой предыдущей дуги совпадает с началом следующей, называется путем в орграфе. Путь, проходящий через все вершины и при этом только один раз, называется гамильтоновым. Путь, включающий все дуги графа, и при этом только по одному разу, называется эйлеровым. Полным путем называют любую непрерывную последовательность вершин и дуг, идущих от начальной вершины к конечной. Конечный путь, у которого начальная вершина совпадает с конечной, называется контуром.

Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным.

В экономике чаще всего используются два вида графов: дерево и сеть.

Дерево представляет собой связный граф без циклов, имеющий исходную вершину (корень) и крайние вершины; пути от исходной вершины к крайним вершинам называются ветвями.

Если граф, вообще говоря, не связный, не содержит циклов, то каждая связная его часть будет деревом. Такой граф называется лесом.

В приложении теории графов к практическим задачам дугам (ребрам) графа сопоставляют какие-то числовые характеристики. Например, пропускная способность транспортной магистрали, запас какого-либо ресурса, продолжительность выполнения какой-либо работы и т.д. Таким образом, дугам графа приписаны определенные веса и граф G называется взвешенным.

2. Матричные способы задания графов

Граф может быть представлен как в виде рисунка, так и в виде матрицы. Это бывает необходимо при большом числе вершин и дуг (ребер), когда рисунок теряет свою наглядность. Матричное представление графов используется при исследовании его на ЭВМ.

Пусть имеется граф G, не содержащий петель, имеющий n вершин и m дуг (ребер). Графу G можно сопоставить матрицу инциденций графа G. Строки m этой матрицы соответствуют вершинам, столбцы n – дугам (ребрам) графа. Если граф ориентированный, то элементы aB_ijBматрицы инциденций равны: (-1), если дуга u исходит из i-й вершины; (+1), если дуга заходит в i-ю вершину. Если граф неориентированный, то элементами матрицы будут 1 и 0. На рис. 1.2 показаны орграф и его матрица инциденций, на рис. 1.3. - неориентированный граф и матрица инциденций.

	uB1B uB2B uB3B uB4B uB5B uB6B uB7B xB1B -1 0 0 0 -1 -1 0 xB2B 1 -1 0 0 0 0 0 xB3B 0 0 0 1 1 0 -1 xB4B 0 1 1 0 0 0 0 xB5BBB 0 0 -1 0 0 1 1

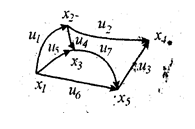
Рис.1.2

	uB1B uB2B uB3B uB4B uB5B uB6B uB7B xB1B 1 0 0 0 1 1 0 xB2B 1 1 0 0 0 0 0 xB3B 0 0 0 1 1 0 1 xB4B 0 1 1 0 0 0 0 xB5B 0 0 1 0 0 1 1

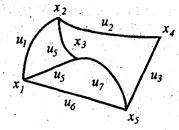
Рис.1.3

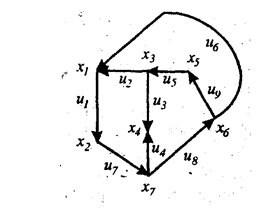
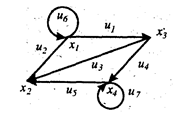
Для ориентированных и неориентированных графов можно сформировать матрицу смежности вершин. Пусть орграф G содержит n вершин. Его матрица смежности представляет собой квадратную матрицу n-го порядка. Строки и столбцы этой матрицы соответствуют вершинам орграфа G. Элементы uB_ijBесть число дуг, выходящих из i-й вершины и входящий в j-ю. В орграфе, не содержащем параллельных дуг, элементами матрицы будут 1 и 0. На рис. 1.4. представлен орграф и его матрица смежности вершин. Как видно из рис. 1.5, у неориентированного графа матрица смежности вершин будет симметрической. По матрице смежности вершин определяется степень вершины, т.е. число дуг, пересекающихся в этой вершине. Число входящих в i-ю вершину дуг равно сумме элементов i- го столбца; число дуг, исходящих из данной вершины, равно сумме элементов i-й строки.

	xB1B xB2B xB3B xB4B xB5B xB6B xB7B xB1B 0 1 0 0 0 0 0 xB2B 0 0 0 0 0 0 1 xB3B 1 0 0 1 0 0 0 xB4B 0 0 0 0 0 0 1 xB5B 0 0 1 0 0 0 0 xB6B 1 0 0 0 1 0 0 xB7B 0 0 0 1 0 1 0

Рис.1.4

	xB1B xB2B xB3B xB4B xB1B 1 1 1 0 xB2B 1 0 1 1 xB3B 1 1 0 1 xB4B 0 1 1 1

Рис.1.5

Граф G также может быть задан матрицей смежности дуг (ребер). Предположим, что некоторый граф имеет m дуг (ребер). Его матрица смежности дуг (ребер) представляет собой квадратную матрицу m-го порядка. Строки и столбцы матриц соответствуют дугам (ребрам) графа. Элементами pB_ijBматрицы для ориентированного графа буду 1 и 0. Если дуга uB_{1 B}прямо предшествует дуге _BuB_jB,B _Bто pB_ijB= 1 и 0 – в остальных случаях. Матрица смежности ребер неориентированного графа своими элементами также имеет 1 и 0. Элемент pB_ijB = 1, если ребра uB_iBи uB_jBсмежные, и 0 – в остальных случаях.